地铁车轮踏面紧急制动热应力分析
2019-03-11周翠,高卿
周 翠,高 卿
地铁车轮踏面紧急制动热应力分析
周 翠,高 卿
河北轨道运输职业技术学院, 河北 石家庄 052165
利用ANSYS软件建立单个地铁车轮带轴有限元模型,考虑第二类边界条件的踏面热流密度值和第三类边界条件表面换热系数,并利用ANSYS热分析瞬态求解器求解车轮在不同时刻的车轮温度,结合铁道部行业标准TB/T 240-1993,对轮轨赫兹接触压力和热应力共同作用引起的车轮进行损伤评价。在仅空气制动下,重点讨论了三种不同紧急制动减速度下,连续两次紧急制动引起的最大温度和对应的等效热应力分布情况,并进行踏面损伤评价。结果表明,最大温度出现在第二次紧急制动过程中;最大温度随着制动减速度的增加而增大;对三种不同减速度工况进行损伤评价得出都符合损伤要求。
ANSYS; 地铁; 制动; 热应力
随着城市经济的发展和人口数量的增加,人们高效的出行关乎着整个城市的生产效率。地铁孕育而生,连接着城市的四面八方,缩短了人们的出现时间。随之而来的问题可想而知,地铁频繁的牵引、制动,车轮踏面与闸瓦之间的不断摩擦,产生高温。特别是紧急制动情况下,列车提供最大的制动力,将对车轮踏面和闸瓦造成严重损伤,对车轮踏面和闸瓦的寿命有着严重的影响。所以有必要对车轮最恶劣的制动情况即紧急制动时车轮踏面产生的温度进行研究。
国内外学者对车轮踏面制动热效应都有一定的研究。在地铁盛行之前,很多研究者主要对重载火车等进行研究。Cameron Lonsdale等[1]重点讨论了重载货车车轮在制动过程中产生的热负荷问题。王京波等[2]利用Marc有限元软件建立了货车车轮有限元模型,研究了闸瓦与车轮摩擦产生的热效应影响。向阳等[3]在货车紧急制动情况下分析了不同轮径所对应的热应力情况。刘俊红等[4]对重在货车踏面制动热响应进行了分析。刘云等[5]利用数值方法建立了货车车轮热应力场的二维模型。侯耐等[6]则对重载货车在长大下坡道的紧急制动工况及逆行了踏面热效应研究。随着近几年地铁的发展,关注地铁研究者也陆续增加。Teimourimanesh等[7]针对地铁车轮不同辐板进行了研究,主要讨论了温度和疲劳强度等问题。杨智勇等[8]以北京地铁10号线为研究对象,对踏面制动热流密度进行推导,建立了车轮制动过程瞬态温度场和应力场三维有限元模型。尹志凯等[9]则利用Marc有限元软件建立了闸瓦和车轮的三维接触模型,讨论了踏面温度和应力。张琪等[10]对不同地铁车轮结构几何参数下的踏面制动热负荷进行了分析。张萌等[11]对地铁车轮研究,踏面制动热容易引起疲劳裂纹和热裂纹。
无论是重载货车还是地铁车辆,众多的研究者多车轮踏面的制动热进行了各种各样的研究。而本文主要针对某地铁车辆车轮踏面在连续两次紧急制动时产生的热负荷对踏面损伤情况进行研究,重点讨论了不同加速度情况下,产生的热负荷大小以及带来的损伤影响。有助于后续地铁对紧急制动加速度的调整,优化地铁运营。
1 模型介绍
1.1 有限元模型介绍
本文利用ANSYS软件建立了单个地铁车轮带轴有限元模型,轮径为840 mm,车轮踏面为LM类型,如图1所示。利用该模型研究车轮踏面紧急制动的制动热,并对其进行分析和评估。制动过程,热传导问题第二类边界条件将被考虑为车轮踏面与闸瓦接触有热流输入的边界;除轴和有热流输入的边界以外的车轮,其他表面全部为热传导问题第三类边界条件。在进行应力场分析时采用顺序耦合法分析热机耦合问题即先用只具有温度自由度的热分析单元分析计算车轮瞬态温度场,得到计算结果后把热分析单元直接转换为对应的具有位移自由度的结构分析单元,再把温度场作为已知温度载荷加载在车轮上,分析计算车轮在摩擦热载荷作用下的结构响应。

图 1 地铁车轮带轴有限元模型

图 2 赫兹轮轨接触模型
为了对车轮踏面损伤进行评价,需计算最大轮轨接触压力p,如图2赫兹轮轨接触模型所示。具体公式如下。

式中,,分别为椭圆接触斑的短半轴和长半轴;为轮重。短半轴和长半轴计算公式如下。

式中,常数和取决于车轮和钢轨曲面的主曲率大小以及两曲面的主曲率平面间的夹角;系数和与和有关。*由下式给出:
式中,1和2分别为车轮和钢轨的弹性模量;1和2分别为车轮和钢轨的泊松比。
1.2 热分析计算
本文为了求出紧急制动过程中的热负荷,需要对第二类边界条件的踏面热流密度值进行求解,在此过程中,采用了能量换算法。制动过程中,假设动能全部转化为热能。而正常的紧急制动过程中,由于存在轮轨摩擦和空气阻力等因素,制动时产生的动能只能有一部分转化为热能,而转化的热能只有部分被车轮重吸收,部分被闸瓦吸收,所以踏面的热流输入必须考虑在车轮和闸瓦之间的分配问题。紧急制动过程中,考虑到车轮转速较高,所以假设摩擦热在车轮踏面均匀分布。整个制动过程可由以下公式求解[12]。
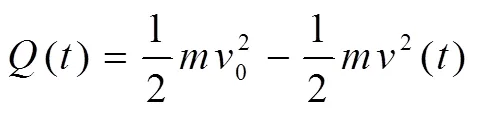

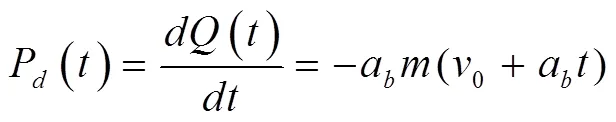


式中,公式(2)为车轮与闸瓦摩擦产生的能量,为车轮质量,0为制动初速度,a为制动减加速度,为制动时间。式(4)为热流率,式(5)为热流密度,为热流分配系数,为踏面摩擦环带面积,λ、λ、a和b分别是车轮和闸瓦的导热系数和导温系数。根据文献[12],取热流分配系数=0.91。
确定了车轮热分析的三类边界条件后,采用ANSYS热分析瞬态求解器求解车轮在不同时刻的车轮温度,由此可以得到车轮踏面在整个制动过程中最高温度部位处的时间—温度曲线,以及在整个制动过程中车轮温度最高时刻的车轮温度场。采用顺序耦合法可以计算得到车轮踏面热应力。
2 计算结果分析
2.1 计算参数
为了探究地铁车轮连续两次紧急制动时踏面温度变化情况,优化车辆制动情况,因此利用ANSYS建立了单个地铁车轮带轴模型,考虑该模型为新轮,最高时速为80 km/h,讨论了三种紧急制动减速度,分别为1.0 m/s2、1.2 m/s2、1.4 m/s2。其他具体参数如下表1所示。

表 1 紧急制动求解参数
2.2 ANSYS计算结果
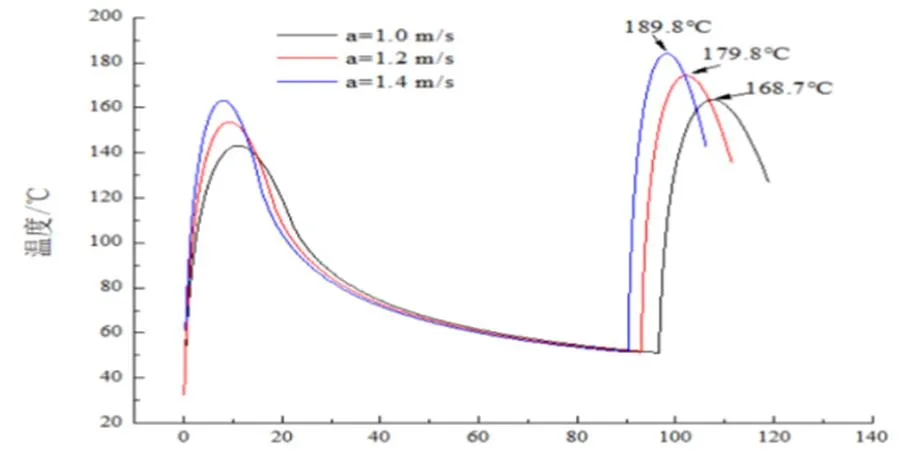
图 3 两次紧急制动时间—温度曲线
图3给出了三种制动减速度工况下两次紧急制动时间—温度曲线图。从图中可以看出,最高制动温度出现在第二次制动过程中。制动减速度越大,制动产生的温度越高。首先车辆减速制动,在制动刚开始时,车辆运行速度相对较大,此时车轮踏面热流密度输入随着制动时间的增加而增大,且制动产生的热量大于对流交换的散热,在这一阶段车轮温度随着制动时间的增加而升高。随着速度的减小,车轮踏面的热流密度输入减小,当车轮表面的对流交换散热大于车轮踏面热流输入产生的热量时,车轮温度开始降低,这使得车轮踏面温升峰值出现在车轮制动过程中。
图4、图5和图6分别为制动减速度为1.0 m/s2、1.2 m/s2、1.4 m/s2时,连续两次紧急制动的最大温度分布与对应的等效热应力分布。ANSYS云图直观地给出了两次紧急制动时的踏面温度和应力变化情况。从图(a)可以看出,最大温度出现在车轮与闸瓦接触的位置,最大温度分别为168.7℃,179.8℃,189.8℃,车轮其他部位温度基本没有变化。对应的最大温度的等效热应力同样出现在车轮与闸瓦接触的位置,其值分别为202 MPa,223 MPa,243 MPa,轮辋与辐板交接处出现较大的等效热应力,车轴受影响最小。三种制动减速度的结果图对比可知,随着减速度的增加,制动最大温度和对应的等效热应力随之增大。

(a) 连续两次紧急制动最大温度 Max temperature from emergency braking for successive two times;(b)连续两次紧急制动等效热应力 Equivalent thermal stress from emergency braking for successive two times

(a)连续两次紧急制动最大温度 Max temperature from emergency braking for successive two times;(b)连续两次紧急制动等效热应力 Equivalent thermal stress from emergency braking for successive two times

(a)连续两次紧急制动最大温度 Max temperature from emergency braking for successive two times; (b)连续两次紧急制动等效热应力 Equivalent thermal stress from emergency braking for successive two times
3 损伤评价
文献表明,现在国内外没有踏面制动车轮最高温度的统一评价标准。根据车轮材料特点,当踏面温度超过奥氏体相变临界温度后,车轮踏面材料将出现奥氏体。当踏面温度快速冷却后,奥氏体将转变为脆硬马氏体,马氏体组织在车轮后继滚动过程中容易导致车轮踏面剥离脱落,加速车轮磨损,所以要求车轮踏面最高温度低于相变温度。我国铁道部行业标准《货车高摩擦系数合成闸瓦》(TB/T 240-1993)要求车轮踏面温度不得超过400℃。根据文献[8]可知,评价轮轨赫兹接触压力和热应力共同作用引起的车轮损伤,如下图7所示。A是常用制动区,B为稀有制动区,C是危险区。表2为车轮踏面损伤评价表。

表 2 车轮踏面损伤评价表
从图7中可以看出,三种紧急制动减速度工况下,都没有达到危险区C,踏面损伤都满足使用要求。但随着减速度增加,有逐渐向危险区C靠近的趋势。所以选择合适的制动减速度有利于车轮踏面最大温度和等效热应力的控制,延长车轮的使用寿命。

图 7 最大热应力评价
4 结 论
利用ANSYS软件建立了单个地铁车轮带轴有限元模型,在仅空气制动时,考虑车辆运行时速80 km/h条件下不同紧急制动减速度对车轮踏面最大温度和对应等效热应力的影响,并对踏面进行损伤评价,得出以下结论。
(1)新车轮在连续两次紧急制动过程中,最大温度出现在第二次紧急制动,同时对应的等效热应力为最大;
(2)随着制动减速度的增加,踏面最大温度和对应的等效热应力随之增加;
(3)三种制动减速度工况下,在损伤评价时都满足运行要求;
(4)选择合适的制动减速度有利于车轮踏面最大温度和等效热应力的控制,延长车轮的寿命。
[1] Lonsdale C,刘敬辉,马大炜.重载货车车轮热负荷问题的探讨[J].国外铁道车辆,2005,42(6):32-37
[2] 王京波.合成闸瓦对车轮热影响的研究[J].铁道机车车辆,2003,23(s2):74-79
[3] 向阳,傅茂海,马鹏,等.30 t轴重货车车轮热应力分析[J].铁道机车车辆,2010,30(6):29-32
[4] 刘俊红.重载货车踏面制动热响应分析研究[D].成都:西南交通大学,2006
[5] 刘云.提速货车车轮的温度场及热应力场数值模拟[D].北京:北京交通大学,2004
[6] 侯耐.重载货车车轮踏面制动热负荷研究[D].成都:西南交通大学,2011
[7] Teimourimanesh S, Vernersson T,Lundén R. Thermal capacity of tread-braked railway wheels. Part 1: Modelling[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2016,230(3):784-797
[8] 杨智勇,韩建民,李志强,等.北京地铁10号线制动热响应分析与评估[J].北京交通大学学报,2012,36(4):159-163
[9] 尹志凯,张军,王春艳.地铁车辆制动时车轮闸瓦热-机耦合分析[J].大连交通大学学报,2015,36(4):14-17
[10] 张琪.不同地铁车轮结构几何参数下踏面制动热负荷分析[J].计算机辅助工程,2016,25(2):19-24
[11] 张萌.北京地铁车辆车轮常见失效类型及其对策[J].铁道机车车辆,2013,33(3):81-84
[12] 贾世平.地铁车辆转向架制动动态温升特性研究[D].上海:同济大学,2007
Analysis on Thermal Stress from Metro Wheel Tread Emergency Braking
ZHOU Cui, GAO Qing
052165,
The finite element model of a single Metro wheel with axle is established by using ANSYS software. The tread heat flux of the second boundary condition and the surface heat transfer coefficient of the third boundary condition are taken into account. The wheel temperature of the wheel at different time is solved by using ANSYS thermal analysis transient solver. Combining with the industry standard TB/T 40-1993 of the Ministry of Railways, the wheel-rail Hertz is calculated. The wheel damage caused by contact pressure and thermal stress is evaluated. Under the condition of air braking only, the maximum temperature and equivalent thermal stress distribution caused by two consecutive emergency braking under three different emergency braking decelerations are discussed, and the read damage is evaluated. The results show that the maximum temperature appears in the second emergency braking process; the maximum temperature increases with the increase of braking deceleration; the damage evaluation of three different deceleration conditions is in line with the damage requirements.
ANSYS; metro; braking; thermal stress
U231+.94
A
1000-2324(2019)01-0057-05
10.3969/j.issn.1000-2324.2019.01.012
2018-01-23
2018-03-05
周翠(1971-),女,硕士,高级工程师,研究方向:轨道交通运输及车辆. E-mail:zhouc88.good@163.com
