聚乙烯醇薄膜中茶多酚向水中释放的不同动力学模型比较分析

陈晨伟，许哲玮，马亚蕊，谢 晶,*，张勤军，唐智鹏，杨福馨

（1.上海海洋大学食品学院，上海 201306；2.上海水产品加工及贮藏工程技术研究中心，上海 201306；3.农业部水产品贮藏保鲜质量安全风险评估实验室（上海），上海 201306；4.食品科学与工程国家级实验教学示范中心（上海海洋大学），上海 201306）

随着食品包装技术的不断发展，活性包装薄膜材料作为一种非常具有发展前景的包装技术，已经受到国内外研究人员的广泛关注。释放型食品活性包装薄膜是活性包装薄膜材料的一种，是指将抗菌剂、抗氧化剂等活性物质加入塑料薄膜材料中，在食品贮藏过程中能从薄膜内向食品中释放出活性物质，延长食品货架寿命、改进感官品质、提高食品安全性，从而维持食品品质[1]。

聚乙烯醇（poly-(vinyl alcohol)，PVA）是一种多羟基的合成高分子聚合物，具有优异的生物相容性、成膜性、透明性、气体阻隔性、可降解性等优点[2-4]，被广泛应用于包装材料、医药等领域，已被美国农业部批准用于肉类、家禽类食品的包装[5]。因此，国内外学者开展了大量以PVA为基材的活性包装薄膜研究，制备得到含不同类型活性物质的具有抗菌、抗氧化性能的包装薄膜[6-14]，延长了奶酪、牛肉、鳊鱼等食品的货架期[15-18]。对于释放型活性包装薄膜，其抗菌/抗氧化功能性的实现是基于活性物质从薄膜基质向食品中的扩散作用。因此，在抗菌/抗氧化包装薄膜的开发过程中，掌握薄膜中活性物质的释放规律极其重要。食品是一个多成分的复杂体系，为方便研究，常用食品模拟物代替真实食品来进行薄膜中活性物质的释放规律研究，如欧盟法规中规定以10%（体积分数，下同）乙醇溶液、3%醋酸溶液、20%乙醇溶液及50%乙醇溶液、植物油和聚2,6-二苯基苯乙烷（60～80 目、200 nm）食品模拟物分别代表水性、酸性、含酒精类、高脂肪类和干性食品[19]。大量学者通过释放实验研究了薄膜在不同食品模拟物体系中活性物质的释放性能，并通过动力学模型揭示其释放规律[20-23]。常用的动力学模型有Fickian模型[20-22]、Fickian＋一级动力学模型[23]、Weibull模型[24]和短期释放模型[21]，其中Fickian模型应用最为广泛。

目前大部分动力学模型研究都是基于某一种模型对薄膜在食品模拟物中活性物质的释放规律进行表征，评价模型的拟合效果，而鲜有采用不同动力学模型对其释放规律进行表征及比较分析的相关报道。本研究通过释放实验探究了PVA薄膜中茶多酚（tea polyphenols，TP）向水中的释放规律，比较分析了4 种不同动力学模型对茶多酚释放规律的表征，为研究活性包装薄膜在水性食品模拟体系中活性物质的释放规律提供理论依据。

1 材料与方法

1.1 材料与试剂

100-27 1799型PVA树脂（分子质量70 000～85 000 Da，聚合度1 700，醇解度99%） 中国石化上海石油化工股份有限公司；茶多酚（纯度≥98%） 郑州景德化工产品有限公司；丙三醇、无水碳酸钠、硼酸、冰乙酸、无水乙醇、福林-酚试剂 国药集团化学试剂有限公司。

1.2 仪器与设备

UTP-313电子天平 上海花潮电器有限公司；安全智能型反压高温蒸煮锅 北京发恩科贸有限公司；LHS-150HC-II恒温恒湿箱、DZF-6030A真空干燥箱 上海一恒科学仪器有限公司；AZY-SERIES加热台 深圳市安卓源科技电子有限公司；DF-101S集热式恒温加热磁力搅拌器 邦西仪器科技（上海）有限公司；UV-2100型紫外-可见分光光度计 尤尼柯（上海）仪器有限公司；超声波清洗器 上海科导超声仪器有限公司。

1.3 方法

1.3.1 包装膜制备

参照前期研究的方法[25]，采用溶液流延法制备得到3 种含不同质量分数（分别占PVA树脂质量的0.5%、2.0%、4.0%）茶多酚的PVA活性薄膜，分别标记为PVA-0.5TP、PVA-2.0TP和PVA-4.0TP，将其装入高阻隔袋中抽真空密封后放入干燥器内备用。

采用螺旋测微仪测量薄膜厚度；通过天平称取薄膜质量，计算得到薄膜的密度。PVA-0.5TP、PVA-2.0TP和PVA-4.0TP薄膜测得的厚度分别为（0.058±0.001）、（0.059±0.002）mm和（0.058±0.001）mm，测得的密度分别为（1.308±0.010）、（1.301±0.011）g/cm3和（1.305±0.007）g/cm3。

1.3.2 释放实验

1.3.2.1 薄膜中茶多酚质量浓度的测定

将厚度相近且均匀的薄膜样品裁切成40 mmh40 mm，取6 片薄膜样品加入含50 mL 75%（体积分数，下同）乙醇溶液的棕色玻璃瓶中，在45 ℃、40 Hz下超声处理120 min。采用福林-酚法，将1 mL待测液加入5 mL质量分数10%福林-酚溶液中，摇匀并在3～8 min后加入4 mL质量分数7.5%碳酸钠溶液，摇匀并在室温下静置60 min，在765 nm波长处测定吸光度，做3 个平行试样，取平均值，计算得到茶多酚质量浓度。将薄膜取出，沥干后加入新的50 mL 75%乙醇溶液中，重复上述步骤，测定待测液中的茶多酚质量浓度；重复以上操作直至待测液中的茶多酚质量浓度足够小（不超过5h10－5g/100 mL），最后将各次测得的质量浓度经计算相加得到薄膜中茶多酚的总量[26]。

1.3.2.2 薄膜中茶多酚向水中释放量测定

以水为食品模拟液，将厚度相近且均匀的薄膜样品裁切成40 mmh40 mm，取12 片薄膜样品加入100 mL水中，密封避光放置于25 ℃环境中，间隔一定时间（0～0.5 h时，每间隔10 min取样；0.5～3.0 h时，每间隔30 min取样；3.0～8.0 h，每间隔60 min取样；之后每间隔24 h取样）从中移取1 mL模拟液，采用1.3.2.1节福林-酚法测定其吸光度，做3 个平行试样，取平均值，经计算得到该时刻水中茶多酚的释放量。

1.3.3 释放动力学模型的建立

1.3.3.1 Fickian模型

Fickian第二定律常被用来模拟食品接触材料中活性物质的释放行为。在释放实验中，根据包装材料体积与食品/模拟液体积之间的关系，Fickian模型可以分为有限包装-无限食品模型和有限包装-有限食品模型。由于本释放实验中包装材料的体积与食品体积相比是不可忽略的，所以选择有限包装-有限食品模型，方程分别如式（1）、（2）所示。

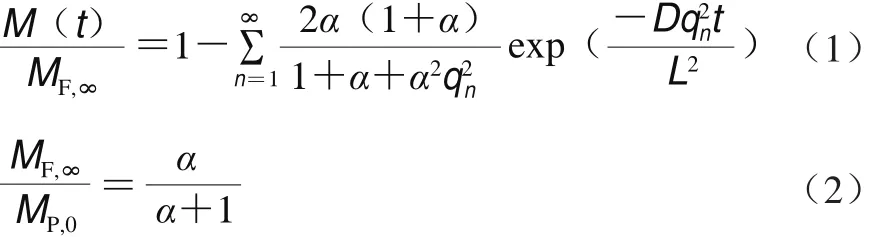
式中：qn为方程tan qn＋αqn＝0的非零正根；M（t）为茶多酚在t时刻从薄膜中释放到食品模拟液中的释放量；MF,∞为平衡时茶多酚从薄膜中释放到食品模拟液中的释放量；MP,0为薄膜中茶多酚的总量；D为薄膜中茶多酚的扩散系数；L为薄膜的一半厚度；α为释放平衡时食品模拟液中茶多酚质量浓度与薄膜中茶多酚质量浓度的比值；M（t）/MP,0为释放率。

1.3.3.2 Fickian＋一级动力学模型

有研究发现，低分子质量化合物在聚合物中的扩散通常由两种同时发生的现象所支配：一种是随机现象（与布朗运动有关），渗透流完全由浓度梯度驱动；另一种是由局部系统的距离驱动的松弛现象[23]。与布朗运动有关的传质通常用Fickian模型描述，由距离驱动的薄膜结构松弛可用一级动力学方程描述，分别如式（3）、（4）所示。

式中：MF（t）为由浓度梯度驱动的随机现象引起的茶多酚在t时刻从薄膜中释放到食品模拟液中的释放量；MR（t）为由距离驱动的薄膜结构松弛现象引起的茶多酚在t时刻从薄膜中释放到食品模拟液中的释放量；XF为茶多酚的释放机制偏离理想Fickian定律的衡量参数，XF＝1时方程（4）为Fickian模型，XF＝0时为反常扩散；τ为与聚合物弛豫相关的弛豫时间。

1.3.3.3 Weibull模型

Weibull分布在描述复杂的动力学方面表现了优异的模型性能，已有研究使用该模型表征了聚己二酸/对苯二甲酸丁二酯薄膜中乳酸链球菌肽向水中的释放动力学[24]，方程如式（5）所示。

式中：b为尺度参数；k为形状因子。

以上方程以包装材料中的活性物质含量变化为参数，将其转化为以食品模拟液中的活性物质含量变化为参数，方程如式（6）所示。

1.3.3.4 短期释放模型

在活性物质的释放过程中，当M（t）/MF,∞＜0.67时，活性物质的释放可由Fickian模型的简化方程来表征[26]，并被文献[18]证实该短期释放模型具有一定的可靠性，方程分别如式（7）、（8）所示。

1.4 数据处理

实验数据处理、作图采用Matlab 2014a、Origin 8.0软件，模型参数由Origin 8.0软件对不同释放动力学模型和实验数据进行非线性拟合计算得到。

2 结果与分析

2.1 薄膜中茶多酚向水中的释放规律分析

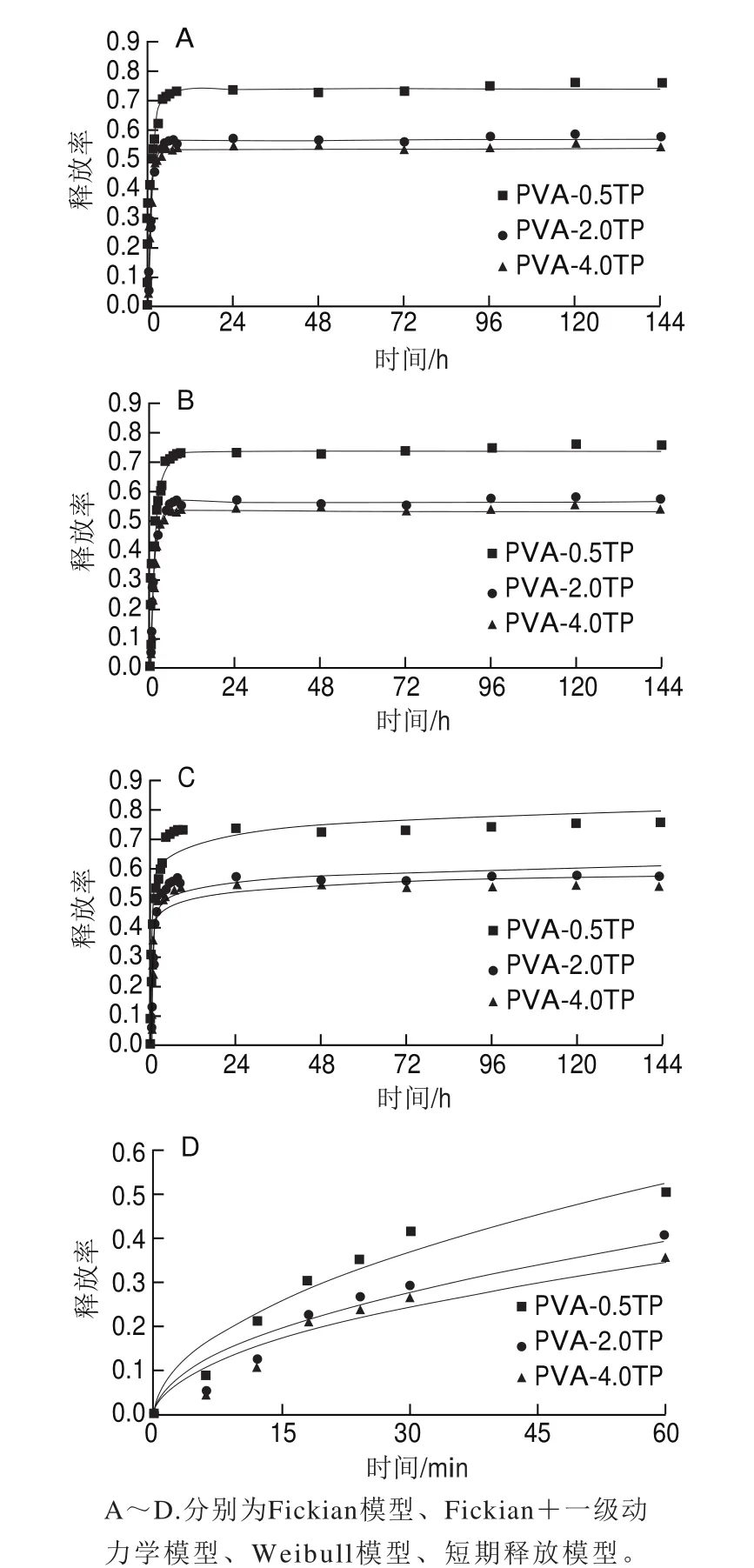
由图1可知，薄膜中的茶多酚向水中释放时初期释放速率较快，然后释放趋于平缓，约8 h后达到平衡状态。PVA薄膜中的茶多酚质量浓度越高，水中的茶多酚平衡质量浓度也越高，但其释放率越低。这可能是由于茶多酚含有疏水性的苯环基团，随着薄膜中茶多酚质量浓度的增加，薄膜内所含有的苯环基团增加，从而提高了薄膜的疏水性[25]。活性物质从溶胀型薄膜中的释放主要依赖以下3 个方面：1）食品模拟液基质向薄膜中扩散；2）薄膜基材溶胀；3）活性物质通过溶胀薄膜向食品模拟液基质中扩散[27-29]。PVA薄膜具有很强的亲水性，当其与水发生接触时，水分子向薄膜扩散进入薄膜结构中，薄膜吸水后不断溶胀，结构变得松弛，使茶多酚从薄膜中逐渐释放出来，而水中的茶多酚质量浓度逐渐增加，直至达到平衡状态。这也是溶胀型薄膜中活性物质的释放原理，与海藻酸钠膜[20]、蛋白膜[28]等亲水性薄膜中的活性物质释放原理类似。

图1 PVA薄膜中茶多酚在水中的释放规律曲线Fig.1 Release curves of tea polyphenols from PVA fi lms into water

2.2 释放动力学模型比较分析

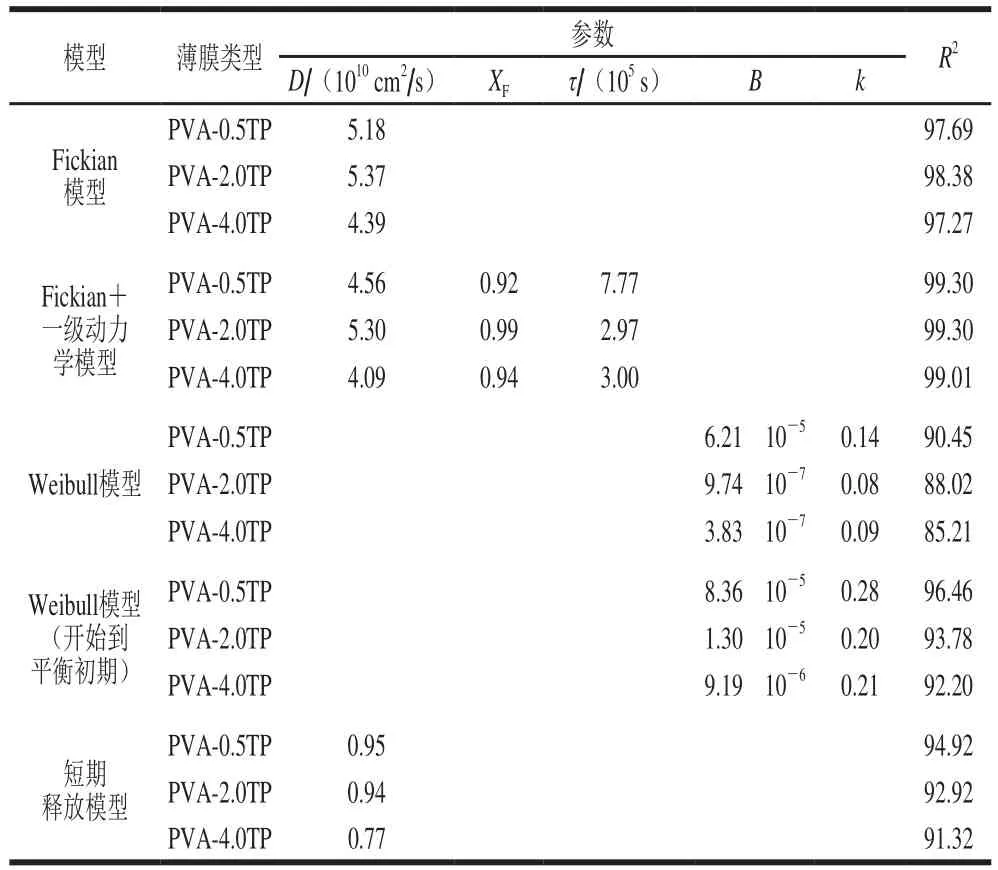
表1 PVA薄膜中茶多酚在水中释放的不同动力学模型参数及其拟合效果评价Table1 Correlational coeff i cients of different kinetic models for the release of tea polyphenols from PVA fi lms into water

根据释放实验所得的数据，分别应用不同的释放动力学模型对PVA薄膜中茶多酚在水中的释放规律进行拟合，对应的模型参数和评价指标如表1所示。对比4 种模型的拟合效果可得，Fickian模型和Fickian＋一级动力学模型拟合效果较好，拟合度（R2）≥97.27，表明这两个动力学模型可以很好地模拟PVA薄膜中茶多酚向水中的释放规律，后者更优（R2≥99.01）。Weibull模型的拟合度稍低（R2≥85.21），表明该模型模拟茶多酚的释放较Fickian模型和Fickian＋一级动力学模型差。短期释放模型的R2≥91.32，表明在M（t）/MF,∞＜0.67时该模型可以较好地模拟茶多酚的释放。

对比Fickian模型和Fickian＋一级动力学模型，后者的拟合度略高（图2），表明其可以更好地模拟PVA薄膜中茶多酚向水中的释放，也进一步表明了茶多酚的释放是随机扩散现象和薄膜结构松弛现象共同作用的结果。当PVA薄膜与水发生作用时，薄膜发生溶胀，聚合物大分子被迫以新的构象重新排列，该过程是导致茶多酚释放机制偏离理想的Fickian扩散行为的主要原因[23,30]。采用两个模型拟合得到的扩散系数（D），其大小均在同一数量级，且数值相差不大，其偏离参数XF≥0.92，表明Fickian＋一级动力学模型中的一级动力学模型对Fickian模型的影响相对较小，进一步表明随机扩散现象在PVA薄膜茶多酚的释放中占主导作用。对比3 种PVA薄膜，含质量分数0.5%茶多酚的PVA薄膜的XF值相对最小，表明该薄膜的结构松弛现象在茶多酚释放中的贡献度在3 种薄膜中最大。此外，D值与薄膜中茶多酚质量分数无明显规律，表明PVA薄膜中茶多酚的质量分数对其释放速率的影响不大。

图3 PVA薄膜中茶多酚向水中释放至平衡状态之前的Weibull模型拟合曲线Fig.3 Fitting curves of Weibull models for the release of tea polyphenols from PVA fi lms into water before reaching equilibrium

对于Weibull模型，如果以刚接近平衡状态之前的实验数据为拟合对象，Weibull模型的R2≥92.2，其拟合曲线如图3所示，表明该模型可以较好地模拟从释放开始到平衡初期之间薄膜中茶多酚的释放。但是Weibull模型中只有形状参数和尺度参数，没有类似Fickian模型和Fickian＋一级动力学模型中的D值来定量表征其释放速率。对于短期释放模型，尽管该模型可以较好地模拟薄膜中茶多酚的短期释放，但是该模型得到的D值与Fickian模型和Fickian＋一级动力学模型不是同一个数量级，且变化趋势不同，表明短期释放模型不适合用于模拟评估该薄膜中茶多酚在整个释放过程中的释放性能。而于文喜等研究发现，采用该模型评估多糖基抑菌膜内山梨酸钾在食品模拟液中的释放规律具有一定的可靠性[21]。因此，针对不同类型薄膜中的活性物质在食品模拟液中的释放不能直接使用短期释放模型来模拟评估。

3 结 论

PVA薄膜中的茶多酚向水中释放时初期释放速率较快，后期渐渐趋于平缓，其释放率随薄膜中茶多酚质量浓度的增加而降低。对比4 种模型的拟合效果，Fickian＋一级动力学模型模拟效果最好，Fickian模型次之，两者均能很好地模拟茶多酚的释放，Weibull模型的拟合效果较前两个模型差，但是该模型可以较好地模拟从释放开始到平衡初期之间释放过程；短期释放模型对短期释放的拟合效果较好，但其扩散系数与Fickian模型和Fickian＋一级动力学模型得到的扩散系数相差较大，不适用于模拟评估PVA薄膜中茶多酚整个释放过程的释放规律。