推力室外壁机器人自适应焊接控制研究
2019-03-08杨瑞康张勤练
杨瑞康,张勤练,周 舟,董 飞
(1.西安航天发动机有限公司,陕西 西安 710100; 2.93956部队,甘肃 张掖 361023)
0 引言
国内外在汽车、航空、航天领域逐渐实现了机器人自动焊接,但国内在液体火箭发动机推力室上机器人焊接技术还应用得很少,焊接过程中参数控制技术应用得更少。焊接控制技术应用难度一般较大,主要因为焊接是模糊科学,焊接参数一般在一定范围内变动,同时焊接质量精准评价困难[1]。现有产品自动焊接时因为产品坡口状态的差异性容易产生局部咬边,余高不均匀,或者未溶透气孔等问题,需要手工再补焊[2]。欧洲、美国NASA、SPACEX等航天企业逐渐应用了焊接过程控制技术,国内航天发动机领域焊接过程自适应控制还没有实际的应用[3-5]。
航天发动机产品焊接质量要求高,由于钣金件热加工带来了坡口状态不稳定、存在间隙等问题。本文结合试验与数值模拟技术,建立了推力室外壁坡口自适应焊接参数模型,输入为对接间隙、坡口宽度,输出为焊接电流、送丝速度与摆动幅度等工艺参数。并在SIMULINK平台下建立了机器人自适应仿真系统,以坡口间隙与坡口宽度为输入量、焊接电流及焊接速度为输出控制量,进行了机器人焊接过程自适应控制系统仿真验证。
1 试验设备及软件
试验设备为机器人热丝TIG焊接系统及SERVE激光焊缝坡口识别系统。相对于传统TIG焊,热丝TIG焊是将填充焊丝进行焊前加热,大大加快了焊丝的熔化速度(增加达20~50 g/min)[6]。
本文采用的SYSWELD焊接有限元软件可用于热温度场模拟、电磁分析、力学分析和氢扩散,同时焊接过程数值模拟采用了生死单元技术[7-8]。焊接工艺参数的调整过程与电弧特性、焊接电源特性等多方面因素相关,为了控制精确且响应快速,本文通过MATLAB SIMULINK平台搭建仿真系统进行研究与验证。

图1 机器人热丝TIG焊接系统Fig.1 Robot heat TIG welding system
2 推力室外壁焊接参数模型建立
2.1 试板焊接试验
进行步长为5 A的变焊接参数热丝TIG焊接试验,记录焊接开始出现缺陷的焊接参数。试验直到未熔透缺陷如图2(a)所示,记录此时的焊接电流Imin,然后将焊接电流不断调大,直到焊漏缺陷如图2(c)所示,记录此时的焊接电流Imax。定义初选参数Im=0.5(Imin+Imax)。

图2 焊接熔合状态Fig.2 Fusion state of welding
同时根据焊接背部熔宽及焊接热输入最终确定优选焊接参数。优化参数需要满足焊缝背面熔宽t最大、热输入W较小,即i={i|ti=maxt},i={i|Wi=minW}。
2.2 焊接参数模型建立及数值模拟
本文通过数值模拟的方式得到熔池面积与电流参数、板厚及焊接速度的关系,在此之前需要调整数值模拟模型,使得数值模拟的结果与试验实测的结果保持一致性,从而准确地进行焊接过程数值模拟计算[9-10]。推力室材料有QCr0.8合金与S-06不锈钢,通过对SYSWELD进行二次开发,建立材料QCr0.8与材料S-06的材料文件。
热丝TIG焊过程中熔池尾端随着两侧液体金属的凝固逐渐变细,熔池头部则是半圆形向前扩展,根据对于热源模型的研究,其中双椭球移动热源模型用来描述这种状态[11],如图3所示。
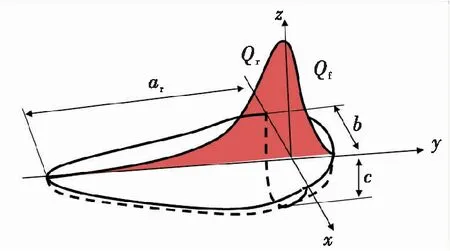
图3 双椭球热源模型Fig.3 Double ellipsoid heat source model
三维非线性瞬态传热问题的控制方程为:
(1)
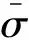
(2)
焊接数值模拟过程包括以下步骤:几何模型建立、网格划分、材料物性参数整理与设置、热源校核、边界条件及约束条件设置、求解方法与参数设置、计算温度场、计算应力场及后处理[14]。提取计算结果,如图4所示。
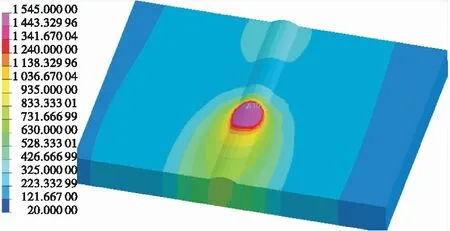
图4 焊接试验试板温度场云图Fig.4 Temperature field of welding test plate
本文为了简化对焊接焊缝尺寸形状的描述,约定:焊缝在垂直于焊接方向的稳定的横截面简称为焊缝截面,其对应的截面积为焊缝截面积。
设计三因素四水平回归试验,探究焊缝截面积与焊接电流、焊接壁厚及焊接速度的关系模型。针对V型60°坡口数值模拟试验,变量为焊接电流100~400 A(打底焊接电流为50~300 A)、板厚5~12 mm与焊接速度10~25 cm/min。数值模拟试验结束后,设定材料熔化温度线(固相线、液相线)后进行后处理。并对熔池区域面积进行计算测量,本文对熔池区域面积测量时定义3个测量值:高度X1,宽度X2及深度X3,如图5所示。
图5 焊缝截面区域测量图Fig.5 Measurement of welding section
通过板件焊接数值模拟进行各个参数的焊接过程计算,得到数据结果如表1所示。
查阅国内外文献在描述多变量单响应量时,通常的方法是建立式(3)所示模型,并根据相关检验法对回归模型进一步进行检验调整:
(3)
式中:w为响应变量(焊缝截面积);β为回归系数;v为焊接工艺参数;ε为残差;k=2。

表1 填充层数值模拟回归试验结果
将表1数据处理求出定义面积后,进行偏最小二乘回归分析,经过多次回归,剔除影响过小的二次项、交叉项后得到填充层焊缝截面积与3个参数的回归公式:
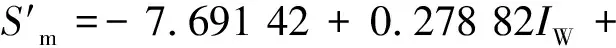
(4)
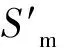
对上述得到的回归方程模型进行显著性检验,可采用F检验法检验回归的总体效果。其F值为52.62,远大于F0.01(8,9)=5.47,回归效果显著;回归方程相关系数R2=98.33%,也表明回归效果非常显著。同样得到打底层焊缝截面积模型与盖面层焊缝截面积模型:
(5)
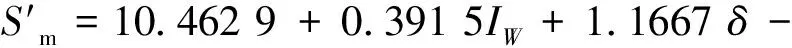
(6)
以上3个模型均是根据S-06钢物性参数所得,1Cr21Ni5Ti的计算焊缝截面积为S-06钢的1.091倍。根据3种近似焊缝截面几何模型圆、椭圆和梯形,计算得出圆、椭圆的弦长等信息,进而获得模型规划焊缝截面积S0。如图6所示,根据焊接填充入金属量及形状(梯形、圆、椭圆)等建立坐标系,计算出椭圆(圆)方程,得出规划焊缝截面宽度、深度(最小的熔透所需熔池区域)所需的焊缝截面积。
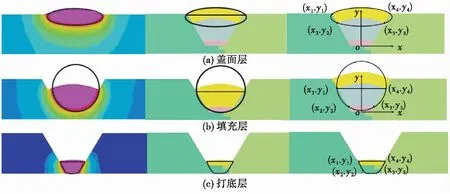
图6 预估焊缝截面形状计算模型示意图Fig.6 Calculation model of estimating welding section shape
焊缝截面按照椭圆与半圆/梯形计算如图6所示。(x1,y1),(x2,y2),(x3,y3)及(x4,y4)为填充规划面积后的层间高度与坡口侧壁交点。其中打底层的梯形焊缝截面区域底部宽设为e。焊缝截面规划面积S0只是焊缝截面积区域规划的最小值,为保证焊接参数的可靠性及稳定性,需对S0公式进行修正,通过乘上一个大于1修正系数实现。此修正系数通过试验拟合得出。定义焊缝熔宽、深熔合修正系数为α,β。通过数据拟合得到熔合修正系数,填充:α=1.132 12,β=1.095 6;盖面:α=1.123 8,β=1.061 2;打底:α=1.084 4,β=1。参数计算模型流程如图7所示。
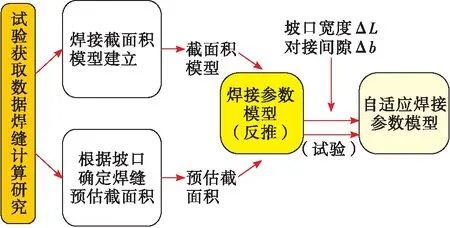
图7 自适应焊接参数模型框图Fig.7 Block diagram of adaptive welding parameter
基于之前的试验研究,推力室及其工装质量很大导致转动惯性较大,难以精确地控制转动速度,故在焊接过程中固定15 cm/min 为常用焊接速度。确定焊接电流、送丝速度与摆幅三者为焊接自适应调整参数,其三者分别可以控制热输入、坡口填入金属量与热源分布,满足焊接过程中需要调整的3个方面。锁底坡口送丝量调整示意图如图8所示,图b中为间隙。
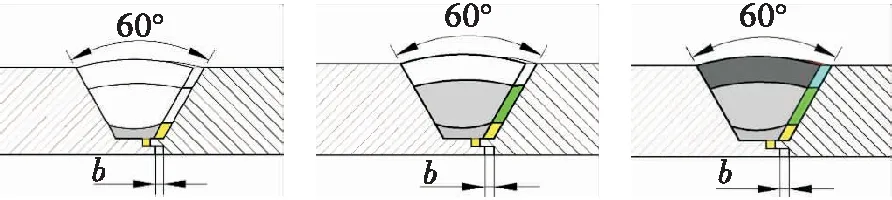
(a)打底层 (b)填充层 (c)盖面层图8 锁底坡口送丝量调整示意图Fig.8 Adjustment of wire feeding amount in the groove
打底层焊接送丝速度(cm/min)求解:
(7)
打底层焊接电流模型求解:
(8)

(9)
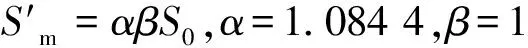
IW=182+23.532 2b+2.117 9b2
(10)
同样得到填充层及盖面层模型:
填充层模型
SW=390+48.412 1b
(11)
IW=283+2.224 4b2+46.089 7b
(12)
盖面层模型
SW=370+39.125b
(13)
IW=274+51.251 6b+5.914 6b2
(14)
As=±(2.5+0.6b)
(15)
2.3 自适应焊接控制系统仿真
传统上,焊接电源采用简单下降的平特性形式, 这种电源简化为一阶惯性环节,即电源电弧系统传递函数与伺服电机驱动的送丝机构传递函数:
(16)
其中
Thd=0.001 2
Khd=22.5
Tm=0.001s
Ts1=0.006
式中Kss为Ud到vs的静态倍率,约为10 mm/S·V。
利用MATLAB SIMULINK仿真平台构建模糊控制模块fuzzy-1,将自适应参数模型嵌入到仿真系统中,进一步建立了焊接电流与送丝速度的自适应控制系统如图9所示,并进行了仿真,得到了优化的各个比例因子的取值。焊接电流控制模糊控制系统的最佳比例因子K3=50;调整因子α1=3,α2=0.2;送丝速度控制模糊控制系统的最佳比例因子K3=800;调整因子α1=4,α2=0.5。
进一步通过使用sin(x)函数作为输入量模拟坡口间隙的变化,进行焊接电流及送丝速度自适应模糊控制算法仿真。如图10所示,该自适应控制系统控制准确性良好,响应速度小于80 ms且无超调现象,可实现自适应焊接参数快速响应控制。
3 试验验证
本文试验验证了推力室扩张段样机及其坡口试验件焊接,焊接结束后,产品焊缝焊接外观良好,无咬边、焊漏等缺陷。
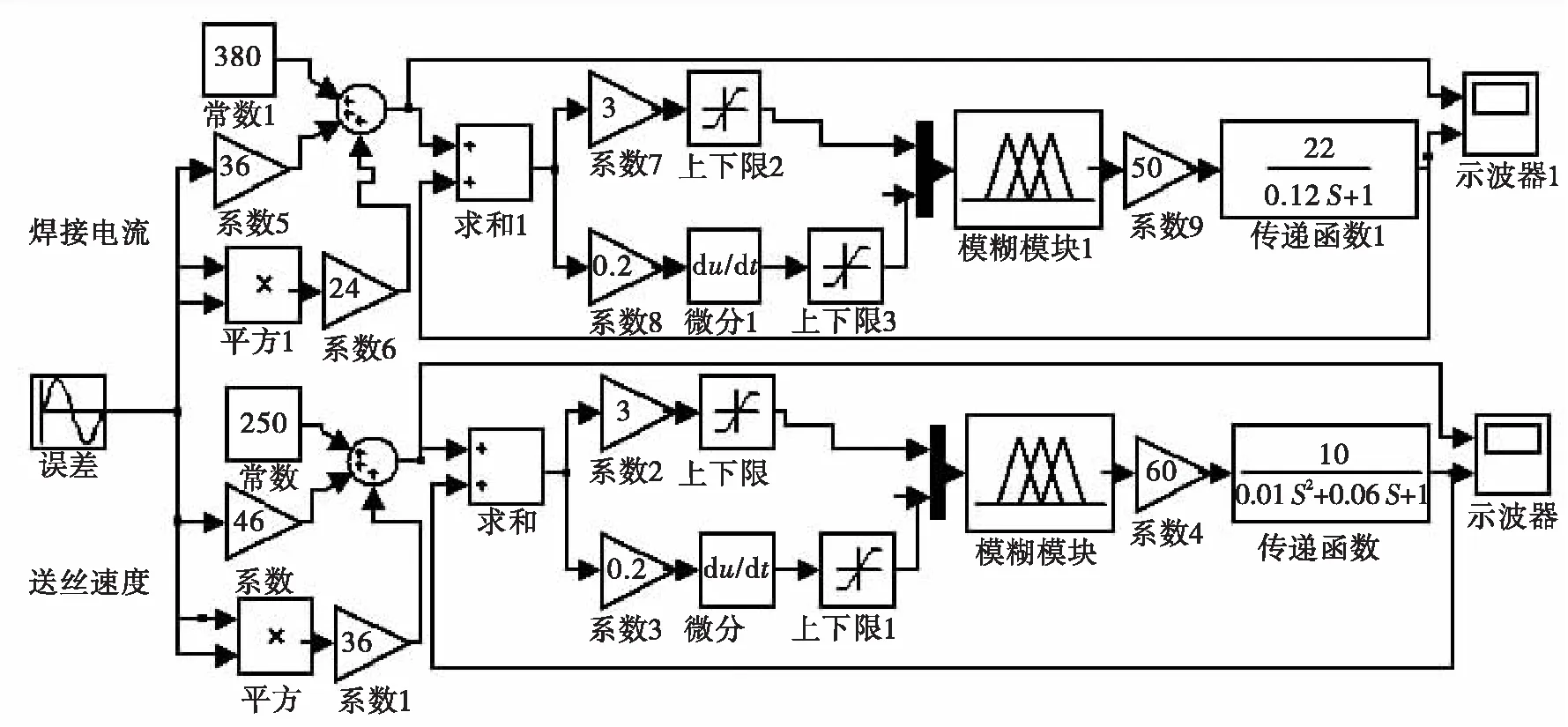
图9 焊接自适应控制系统Fig.9 Welding adaptive control system

图10 焊接自适应系统仿真曲线Fig.10 Simulation curve of welding adaptive system
如图11所示,焊缝余高分别为1.85 mm,1.89 mm及1.88 mm,误差为2%。本试验在推力室锁底坡口宽度波动最大值为1.3 mm情况下焊接一致性良好。进行了推力室坡口的模拟件试验,焊缝熔合良好,并进行X光检测合格。对焊缝拉伸件进行了拉伸试验,两试件断裂位置均发生在热影响区,强度均达到母材强度的90%。

图11 推力室坡口试板自适应焊接试验图Fig.11 Adaptive welding experiment of thrust chamber plate
4 结论
1)建立的推力室外壁坡口焊接参数模型,可实现根据坡口精确计算匹配出焊接电流、送丝速度等关键工艺参数。使得焊接参数能够适应推力室产品对接坡口状态的差异性,实现对不同坡口状态的产品焊接参数根据坡口状态进行调整。
2)针对液体火箭发动机推力室专用材料S06,1Cr21Ni5Ti等材料建立了热丝TIG焊接参数计算模型。可以根据板厚、焊接速度得出合适的焊接参数以及焊接参数窗口。建立板厚、焊接速度、焊接电流与焊缝截面积的参数模型,可以预估计算出焊缝的尺寸。
3)在SIMULINK平台下引入模糊控制建立了机器人焊接自适应系统,针对响应速度仿真优化了调节因子,验证了模型及控制系统的有效性。 采用自适应焊接系统进行了推力室坡口的模拟件试验,焊缝熔合良好,并进行X光检测合格。
