磁锁式双稳态自锁阀响应特性理论研究

尤 罡，王 莉

(1.上海空间推进研究所，上海201112; 2.上海空间发动机工程技术研究中心，上海201112)

0 引言

磁锁式双稳态自锁阀(简称自锁阀)大量应用于空间推进分系统中，将推进剂贮箱(或气瓶)与下游系统进行沟通和故障隔离，实现气、液路的工作管理。自锁阀的显著特点是具有位置自保持功能，其动作过程通常是给驱动线圈施加具有一定幅值和宽度的脉冲电流来改变阀门状态，激励电流消除后，阀门状态靠锁位机构保持不变。自锁阀要实现无源自保持特性，关键在于锁位机构，即通过永磁铁产生无源磁场将阀门保持在开启(或关闭)状态。自锁阀的响应特性是系统的重要指标参数，直接影响推进系统的精确控制。由于自锁阀一般采用双线圈控制，两驱动线圈间存在互感现象，响应特性计算与单线圈控制电磁类阀门有明显区别。本文研究了自锁阀响应特性的理论计算方法及特点。

1 自锁阀控制原理

1.1 自锁阀工作原理

典型的自锁阀结构如图1所示，由开、关驱动线圈、衔铁、永磁铁、吸合台座、阀座和阀芯组件等组件组成。

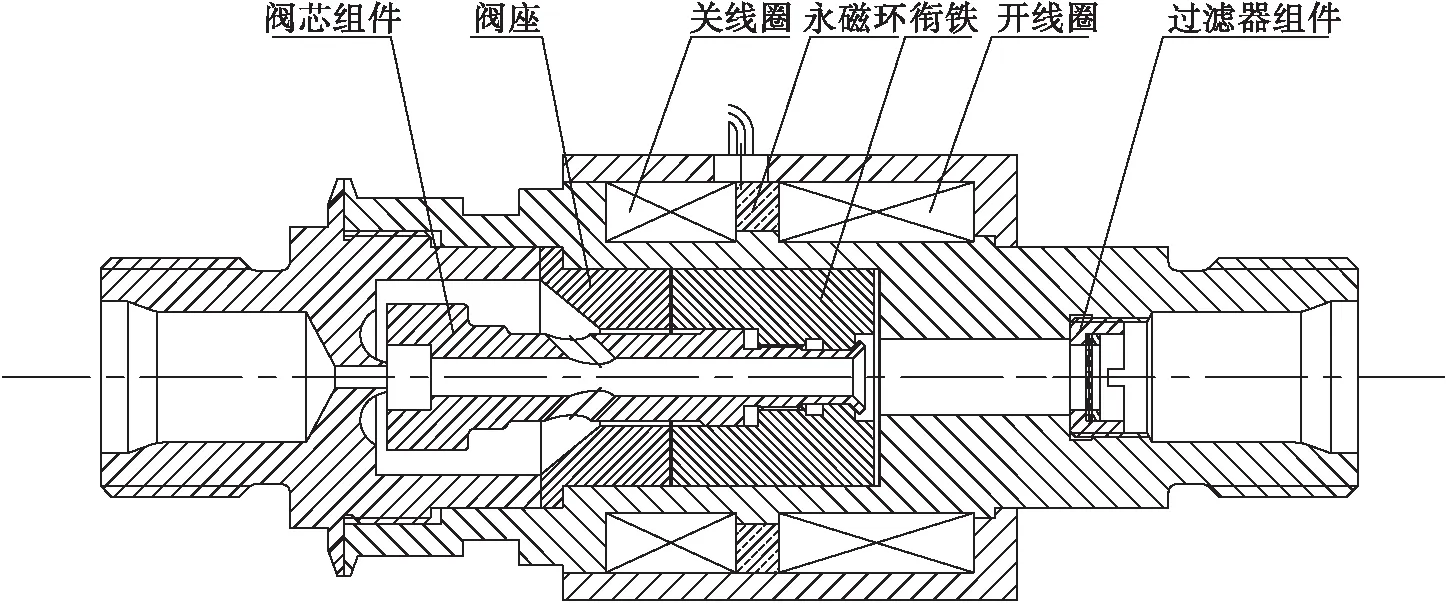
图1 典型自锁阀结构图Fig.1 Schematic of a typical latch valve

工作原理如下：阀门为常闭状态，开线圈通电后，衔铁带动阀芯组件运动到开启位置，开线圈断电，在永磁铁永磁力的作用下，阀芯保持在开启位置；反之，关线圈通电，衔铁带动阀芯组件运动到关闭位置，关线圈断电，阀芯在永磁铁永磁力的作用下保持在关闭位置。

由自锁阀工作原理建立等效磁路模型如图2所示。图2中S为衔铁左右两吸合端面积；φm1,φm2分别为永磁铁在衔铁两端产生的磁通;φe为驱动线圈通电产生的磁通;φig为未通电线圈感应电流产生的磁通;IW为驱动线圈磁势;φig方向与φe相反，与未通电线圈所在吸合端面的φm1方向相同。由等效磁路图可以看出，驱动线圈通电后，当衔铁驱动端面产生的总磁通大于另一端面总磁通时，衔铁开始运动。

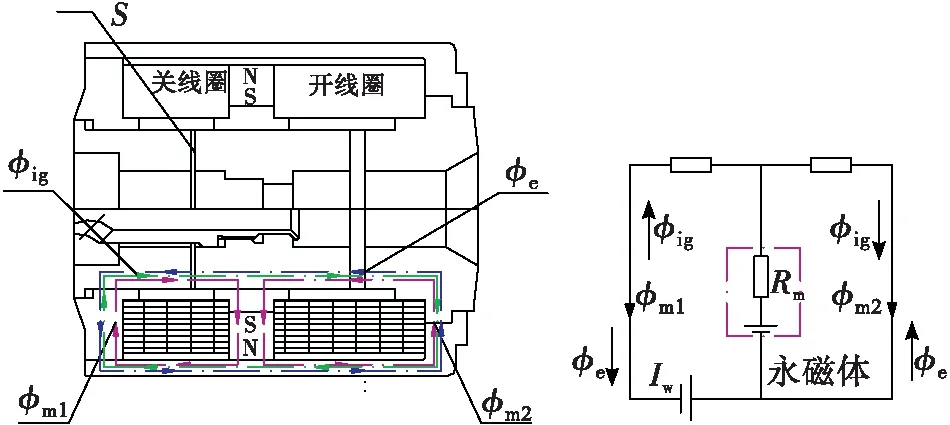
图2 等效磁路模型图Fig.2 Equivalent magnetic circuit models

1.2 自锁阀控制电路

根据自锁阀工作原理和特点(通电时间短，工作电流大)在控制电路中一般采用释放回路(由释放电阻和二极管组成)用于保护控制电路，使自锁阀开、关线圈各自形成一个单向封闭回路。建立由控制电路和自锁阀驱动线圈组成的等效电路模型如图3所示。其中:U为驱动电压；i为驱动电压在通电线圈回路中形成的驱动电流；R1，L1和W1为通电驱动线圈电阻、电感和匝数；ig为未通电线圈回路中产生的感应电流；R2，L2和W2为未通电线圈电阻、电感和匝数；Rf为回路释放电阻；M为两线圈间的互感。自锁阀两个线圈同极条件下一般绕向相反，在互感电路中互为异名端。当一个线圈通电后，另一个线圈产生的电压与原来的电流方向是相反的。

图3 控制电路及等效电路模型图Fig.3 Electrical systems control circuit and equivalent circuit model

2 理论计算模型

自锁阀开启或关闭均为通电吸合作动，动作过程完全相同。响应时间快慢与电流通过线圈绕组变化快慢及绕组电感有关。自锁阀的响应时间电流曲线如图4所示。其中：IW为线圈通电稳态电流；i为衔铁开始运动时的线圈电流。响应时间由触动时间tcd和吸合时间tyd组成，关系式为：

t=tcd+tyd

(1)

图4 自锁阀开启(或关闭)时间与电流曲线Fig.4 Current curve of magnet latch valve when open or close

2.1 触动时间

当线圈通电时，线圈磁场的磁通与永磁铁磁场的磁通互相叠加或抵消，衔铁受力开始发生变化。直到两端面磁通产生的力相等时衔铁处于临界状态，若电流继续增加则衔铁开始运动。从线圈开始通电到衔铁开始运动这段时间为触动时间。合力相等衔铁开始运动时的线圈电流i′即为理论触动电流(假设无感应电流影响，稳态电流IW=U/R1，i′/I则为触动电流比)。

以开线圈驱动为例，由等效电路模型可得出，当驱动线圈通电后磁通随时间变化过程的电压平衡方程为：

(2)

由于驱动线圈总磁链ψ除自身线圈产生的磁链ψ1外，还受到另一个线圈感应电流产生的磁链ψ2影响，因此ψ=ψ1+ψ2；式(2)可变为：

(3)

(4)

由楞次定律可得，异名端感应线圈产生的感应电流与初始线圈电流方向相反，不考虑线圈自感，则释放回路中感应电流为：

(5)

其中

RF=Rf+R2(Ω)

式中：RF为未通电线圈回路中的总电阻；M为开、关线圈的互感;kM为开、关线圈互感耦合系数，与线圈匝数、结构尺寸及相互距离位置有关，一般取0.8～1。

将式(5)代入式(4)可推得最终平衡方程为：

(6)

转化为二阶微分方程：

解方程可求得吸合触动时间为：

(7)

根据自锁阀结构(假设衔铁两端吸合面积相同，不考虑工作介质压力等其他阻力)，衔铁在临界状态时受力状态可以建立力平衡方程：

(8)

而实际情况在有释放回路时需要加入另一线圈感应电流产生磁通的影响(与永磁铁磁通叠加，与驱动线圈磁通抵消)，则力平衡方程调整为：

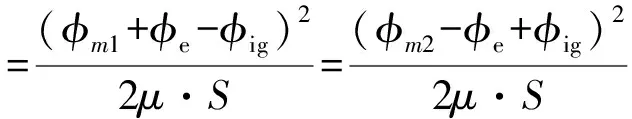
(9)

联立方程(8)～(9)可解得感应电流ig、理论触动电流i′和实际开启电流i的关系为：φe=φe′+φig=iW1=i′·W1+igW2，即：

(10)

同时由电压平衡方程可得双线圈对应的电压方程组为：

(11)

解方程组可得感应电流为：

(12)

假设驱动线圈通电后最终稳态电流IW=U/R1，联立方程(7)、(10)和(12)可建立如下方程组：

(13)

由设计的理论触动电流即可解得实际触动时间、实际触动电流和对应开、关电流比。

2.2 吸合时间

从衔铁开始动作到运动到设计位置的这段时间为衔铁吸合时间，吸合时间计算相对复杂，因为衔铁运动过程中，随着气隙减小而使电感发生变化，且作用在衔铁上反作用力和电磁吸力都在变化。考虑到衔铁行程较小，为使问题简化，假设电磁驱动力在衔铁运动中不变，则可近似按式(14)计算[1]：

(14)

式中:m为衔铁(或运动件)质量，kg；Pw为线圈瞬时功率，Pw=I2R，W；h为自锁阀开度，mm；Kcb为理论触动电流比i′/IW[2-3]。

2.3 响应特性分析

由理论公式可以得出，当自锁阀控制驱动中接入释放回路后，未通电线圈闭合回路产生的感应电流会延长吸合触动时间(如图5中曲线所示)；由式(10)可得自锁阀实际开启(或关闭)电流比i/IW恒大于理论触动电流比i′/IW；当自锁阀驱动回路中没有释放回路时，两线圈间不产生互感电流，理论触动电流比与实际电流比相等；由式(7)与式(12)可得线圈结构参数不变的前提下，电路中的感应电流大小由回路中的释放电阻值决定。释放电阻越小，感应电流越大，吸合触动时间越长，实际开启(或关闭)电流比值相对理论电流比值越大。

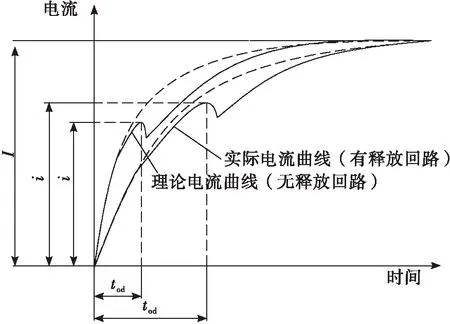
图5 电流曲线对比图Fig.5 Comparison of current curves

也就是说，由于未通电异名端线圈感应电流的影响，自锁阀的开、关动作裕度不再与开启或关闭电流比有直接关联。即使线圈感应电流显著提高了衔铁运动所需要的触动电流值，延长了衔铁的触动时间，但感应电流是随着驱动电流变化而产生，当驱动电流稳定后，感应电流逐渐变小最终趋向于零。理论触动电流比不会随感应电流变化而发生变化，导致自锁阀的动作裕度不会因电流比的变化而受到影响。同理，如果非驱动线圈无闭合回路时(即感应电流为零时)，开启(关闭)电流比就是理论触动电流比。

3 产品测试数据试验验证

以3种成熟型号用典型双稳态磁锁式自锁阀(见图1)为子样，进行理论公式计算和产品测试数据比对。理论计算上，最大程度考虑消除外界影响因素，降低试验误差对计算结果的影响。即确定阀门为空载状态，释放回路电阻值为10 Ω，输入产品设计参数使用MathCAD软件按理论公式进行求解计算；试验数据上，统计了3种与飞行状态相同的所有批次产品(共95台)的测试数据，并选用其中1种自锁阀补充了释放回路电阻50 Ω条件下的响应特性测试。自锁阀响应特性理论计算值与实测试验数据对比情况，如表1所示[4-7]。

表1 响应特性理论计算与实测数据

对比表明，自锁阀响应时间的理论计算值与实测值非常接近；电流比的理论计算值均处于实测中值范围内。同时，考虑到产品的大小不同、试验条件差异等外部因素的影响，可判定理论计算结果与产品实际性能测试情况基本吻合，验证了理论公式的可行性，可在类似结构阀门工程设计分析中应用[8-13]。

4 结论

通过对磁锁式双稳态自锁阀控制方式进行分析，建立电路及磁路等效模型，推导出了自锁阀响应特性计算的简化理论公式。经对子样响应特性的理论计算值和实测数据进行对比，理论公式计算结果与产品实际测试性能基本吻合，验证了简化理论公式的合理性及可行性，可应用于自锁阀设计瞬态特性初步分析工作。另外，通过对自锁阀瞬态特性理论研究及公式推导可以得出：

1)自锁阀控制线圈中，非驱动线圈若形成回路将产生感应电流，对阀门响应特性影响明显，感应电流越大则自锁阀响应时间越长。

2)感应电流会使自锁阀开启或关闭电流比明显增大，但不会影响自锁阀的动作裕度，即当前电流比不再作为自锁阀动作能力的表征属性。