面向工程教育专业认证的《离散数学》课程改革实践

摘要：针对工程教育专业认证中关于“复杂工程问题”的培养要求，对计算机类专业的基础核心课程《离散数学》的教学模式、教学内容、考核形式等进行了相应的改革。通过改革，使得学生的计算机数学理论知识掌握更加扎实，培养了学生解决复杂工程问题能力。

关键词：工程教育认证;复杂工程问题;计算思维;产出导向

中图分类号：G642 文献标识码：A

文章编号：1009-3044（2019）36-0132-02

1概述

《离散数学》课程是计算机科学和其他应用科学的基础理论课，掌握好离散数学的基本理论知识将为后续课程的学习奠定良好的数学基础。根据《华盛顿协议》（Washington Accord，WA）的核心理念“以学生为中心”“产出导向（OBE）”“持续改进”，为了培养学生解决复杂工程问题的能力以及逻辑思维能力，对《离散数学》课程从课程的教学目标、教学模式、考核方式等各方面进行了深入的改革。

2《离散数学》课程特点及对毕业要求指标点的支持

首先，离散数学作为现代数学的一个分支，涵盖数理逻辑、集合论、图论、代数系统、组合数学等多方向内容。在计算机专业中，《离散数学》课程是《数据结构与算法》《编译原理》《数据库原理》课程的重要先修课程，为这些专业基础课程提供了数学理论知识支撑。

在计算机专业课程支撑毕业要求能力指标点课程矩阵中，《离散数学》课程需要支撑指标点1.1、指标点1.2，指标点2.1，指标点2.2，指标点2.3。

3“以学生为中心”混合式教学模式

由于《离散数学》课程概念众多，内容抽象，以往的教学过程中多出现教师满堂灌的现象，将以往的授课过程中的“以教师为中心”转换为“以学生为中心”，提高学生的课堂参与程度。

让学生成为教学的中心，积极采取任务驱动、翻转课堂等教学模式，将培养学生的抽象思维能力、严格的逻辑推理能力以及将实际问题抽象转化为計算机可处理的问题并对其求解的能力作为教学目标。

首先，在课程内容的选择和组织上，围绕学生逻辑思维训练以及解决抽象建模能力培养展开，摒弃烦冗的概念陈述以及死板地讲述定义定理。如，舍弃对图论中关于图的一些延伸的概念，将重点放在学生关于图进行抽象建模的讲授上。

其次，在教学方法上，改变填鸭式教学模式，采用启发式教学方法。如在进行数理逻辑形式化推理证明教学内容时，改变原有的教师“一讲到底”的方式，采用理发师悖论故事、小偷判定等趣味性强的例子，技法学生的学习兴趣，一步步引导学生由浅人深地从本能的逻辑推理过程到符号化的、数学化的推理证明理论。

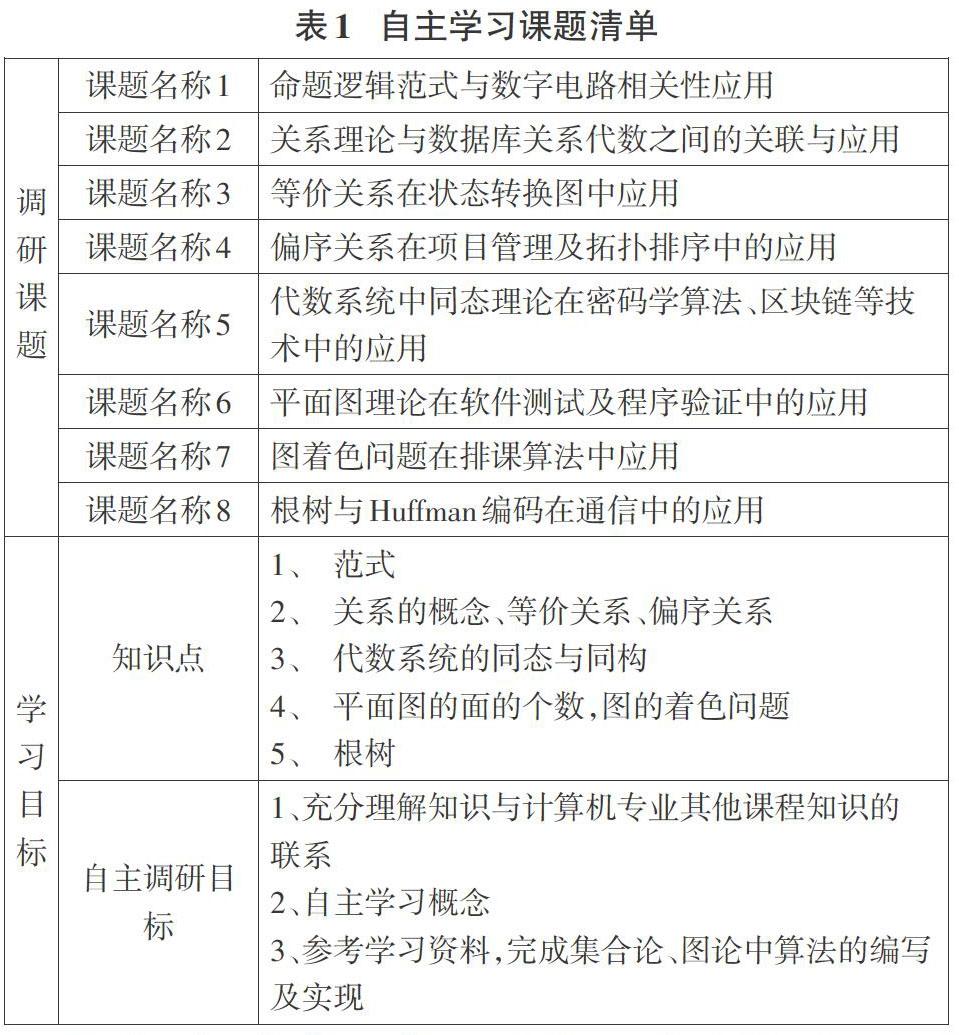
最后，在教学形式上，丰富课堂讲授方式，活跃课堂氛围，对一部分教学内容，适当采用翻转课堂的形式，鼓励学生自主学习。将培养学生解决复杂工程问题的能力作为重点能力进行培养，为此，《离散数学》课程的教学过程中，将和本课程知识点相关的计算机科学中的应用问题转换为学生的自主学习任务以学习小组的形式布置给学生，自主学习课题清单如表l所示：

通过围绕现实理论应用展开的调研活动，让学生主动去探究学习，合作学习，引导学生将离散数学中抽象的知识点转换为具体的计算机应用问题，在实际问题中发现问题，思考问题，理解问题，将理论算法与实际应用相结合，从而更好地完成知识的内化过程。同时，也解决了以往《离散数学》教学过程中，学生缺乏主观能动性，动手能力不强等问题。学生在自主学习的过程中，使得思维方式更加开放，自学能力以及解决复杂工程问题的能力得到了提高。

4《离散数学》考核方式改革

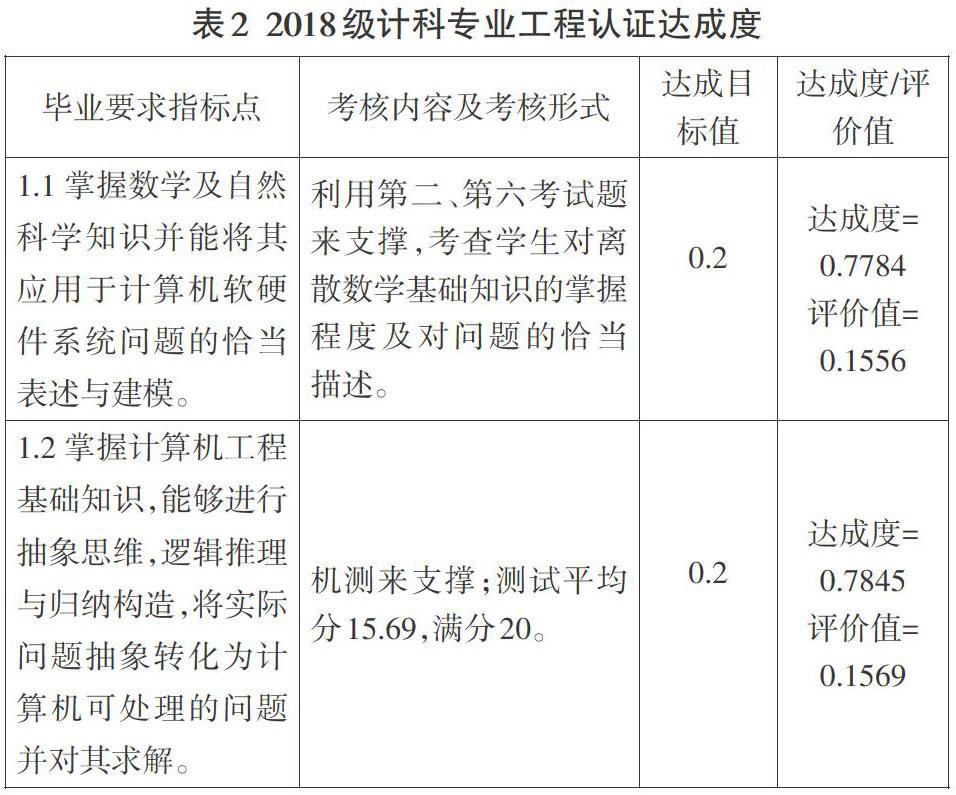
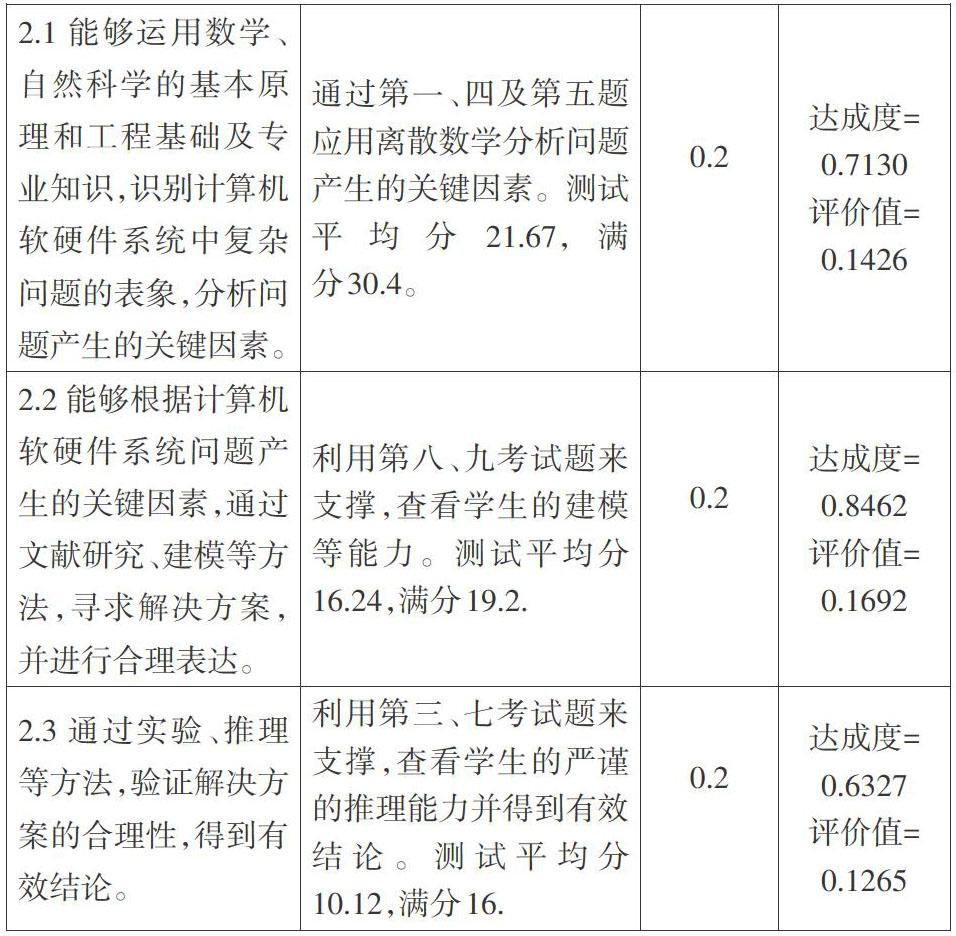
为了培养出具有扎实的能力基础的工科人才，支持、服务和引领行业发展，《离散数学》课程的考核一改单一理论考核形式，将课程实验纳入考核范围，在知识目标考核的基础上添加编程等能力目标的考核。使考核形式更多样化的同时又考查学生代码编写、调试、系统分析等技能。重点考查学生对理论知识的应用程度，使学生能够根据具体的问题抽象出数学模型，进行形式化分析及验证。上机测试题目主要涵盖的知识点有：主析取范式及主合取范式的构造、集合基的判定、函数的判定、最小生成树算法等。通过对18级计科实施该改革，学生的成绩达成情况如表2所示：

通过对学生成绩分析可以看出，《离散数学》课程对工程教育专业认证要求支撑的指标点达成度较好。但是，对于指标点

2.3的达成度低于其他两项。这个主要体现在学生在进行逻辑推理证明时，对形式化证明方法的掌握欠缺。需要在今后的教学过程中，进行强化和持续改进。

参考文献：

[1]左孝凌，李为镒，刘永才.离散数学[M].上海：上海科学技术文献出版社.1982.

[2]蒋宗礼.本科丁程教育：聚焦学生解决复杂工程问题能力的培养[J].中同大学教学，2016（11）：27-30.

[3]林健.如何理解和解决复杂工程问题：基于《华盛顿协议》的界定和要求[J].高等工程教育研究，2016（5）：17-26.

【通联编辑：王力】

收稿日期：2019-10-09

作者简介：孙守卿，山东理工大学计算机科学与技术学院，讲师，研究生学历，研究方向为形式化验证。