图像巧解运动题

华兴恒

对于运动学中的某些问题，只要我们开拓思路，拓展思维空间，则常常可以寻觅到多种解法。因此我们要学会多中选优，优中选快，快中选捷，以期达到快速、简捷获解的目的。往往利用图像求解不失为一种既优又快的解题方法，下面举例分析，也许会对同学们有所启迪。

一、根据题给图像快速解题

【例1】（2012·课标全国卷II）一物块静止在粗糙的水平桌面上，从某时刻开始，物块受到一方向不变的水平拉力作用。假设物块与桌面间的最大静摩擦力等于滑动摩擦力，以a表示物块的加速度大小，F表示水平拉力的大小。能正确描述F与a之间关系的图像是

解析：物块的受力如图2所示，当F不大于最大静摩擦力时，物块仍处于静止状态，故其加速度为0;当F大于最大静摩擦力后，由牛顿第二定律可得F–μFN =ma，即F= μFN + ma，F与a成线性关系，其图像与纵坐标的截距F= μFN。

答案：C

【例2】（2018·全国卷Ⅲ）甲、乙两车在同一平直公路上同向运动，甲做匀加速直线运动，乙做匀速直线运动。甲、乙两车的位置x随时间t的变化如图3所示。下列说法正确的是

A. 在t1时刻两车速度相等

B. 从0到t1时间内，两车走过的路程相等

C. 从t1到t2时间内，两车走过的路程相等

D. 在t1到t2时间内的某时刻，两车速度相等

解析：x - t图像某点的切线斜率表示瞬时速度，则选项A错误;前t1时间内，由于甲、乙的出发点不同，因此路程也不同，则选项B错误;在t1 ～ t2时间内，甲、乙的位移和路程都相等，大小都为x2 - x1，则选项C正确;t1 ～ t2时间内，甲的x - t图像在某一点的切线与乙的x - t图像平行，此时刻两车速度相等，则选项D正确。

答案：C、D

【例3】（2015·全国卷Ⅰ）如图4，一物块在t = 0时刻滑上一固定斜面，其运动的v - t图线如图5所示。若重力加速度及图中的v0， v1， t1均为已知量，则可求出

A. 斜面的倾角

B. 物块的质量

C. 物块与斜面间的动摩擦因数

D. 物块沿斜面向上滑行的最大高度

解析：本题考查了匀变速直线运动、v - t图像和牛顿第二定律。

设物块的质量为m，斜面的倾角为θ，物块与斜面间的动摩擦因数为μ，物块沿斜面上滑和下滑时的加速度大小分别为a1和a2，根据牛顿第二定律有：mg sinθ + μmg cosθ = ma1，mg sinθ - μmg cosθ = ma2。再结合v - t图线斜率的物理意义有：a1 =■，a2 =■。由上述四式可见，无法求m，可以求出θ、μ，则选项B错误、选项A、C均正确;0 ～ t1时间内的v - t图线与横轴包围的面积大小等于物块沿斜面上滑的最大距离，θ已求出，于是可以求出物块上滑的最大高度，则选项D正确。

答案：A、C、D

点评：本题是v - t图像结合牛顿第二定律的综合考查题。解答本题需要掌握v - t图像的物理意义：图像为一直线表示做匀变速直线运动，图像的斜率表示物体运动的加速度，图像与横轴所围面积表示物体的位移。从而根据图像可求出物块沿斜面上滑和下滑过程中的加速度。再根据牛顿第二定律列出物块上滑和下滑过程的动力学方程，联立方程求出斜面的倾角及动摩擦因数。

【例4】（2018·江苏卷）从地面竖直向上抛出一只小球，小球运动一段时间后落回地面。忽略空气阻力，该过程中小球的动能Ek与时间t的关系图像是

解析：设小球抛出瞬间的速度大小为v0，抛出后某时刻t小球的速度为v = v0 - gt，故小球的动能

Ek =■mv2 = ■m （v0 - gt）2，结合数学知识易知选项A正确。

答案：A

【例5】（2019·浙江卷）甲、乙两物体零时刻开始从同一地点向同一方向做直线运动，位移—时间图像如图7所示，则在0 ～ t1时间内

A. 甲的速度总比乙大

B. 甲、乙位移相同

C. 甲经过的路程比乙小

D. 甲、乙均做加速运动

解析：位移—时间图像中，图线斜率大小等于物体速度大小。由图可知，甲做匀速直线运动，乙做变速直线运动，则选项D错误;靠近t1时刻时，乙的斜率大于甲的斜率，即乙的速度大于甲的速度，则选项A错误;在该段时间内，甲、乙物体的初位置和末位置相同，故位移相同，则选项B正确;由于甲、乙物体做的是单向直线运动，故位移大小等于路程，两者的路程也相同，则选项C错误。

答案：B

【例6】（2019·全国Ⅱ卷）如图8所示，在跳台滑雪比赛中，运动员在空中滑翔时身体的姿态会影响其下落的速度和滑翔的距离。某运动员先后两次从同一跳台起跳，每次都从离开跳台开始计时，用v表示他在竖直方向的速度，其v - t图像如图9所示，t1和t2是他落在倾斜雪道上的时刻。则

A. 第二次滑翔过程中在竖直方向上的位移比第一次的小

B. 第二次滑翔过程中在水平方向上的位移比第一次的大

C. 第二次滑翔過程中在竖直方向上的平均加速度比第一次的大

D. 竖直方向速度的大小为v1时，第二次滑翔在竖直方向上所受的阻力比第一次的大

解析：根据v - t图线与横轴所围成的面积表示位移，可知第二次滑翔过程中在竖直方向上的位移比第一次的大，则选项A错误;第二次滑翔过程中在竖直方向的位移比第一次大，又运动员每次滑翔过程中竖直位移与水平位移的比值相同（等于倾斜雪道与水平面夹角的正切值），故第二次滑翔过程中在水平方向上的位移比第一次的大，则选项B正确;根据v - t图线的斜率表示加速度，综合分析可知，第二次滑翔过程中在竖直方向上的平均加速度比第一次的小，则选项C错误;竖直方向上的速度大小为v1时，根据v - t图线的斜率表示加速度可知，第二次滑翔过程中在竖直方向上的加速度比第一次的小，由牛顿第二定律有mg - f = ma，可知第二次滑翔过程中在竖直方向上所受的阻力比第一次的大，则选项D正确。

答案：B、D

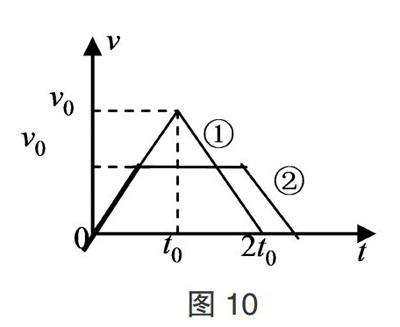
【例7】（2018·全国卷Ⅲ）地下矿井中的矿石装在矿车中，用电机通过竖井运送到地面。某竖井中矿车提升的速度大小v随时间t的变化关系如图10所示，其中图线①②分别描述两次不同的提升过程，它们变速阶段加速度的大小都相同;两次提升的高度相同，提升的质量相等。不考虑摩擦阻力和空气阻力。对于第①次和第②次提升过程

A. 矿车上升所用的时间之比为4 ∶ 5

B. 电机的最大牵引力之比为2 ∶ 1

C. 电机输出的最大功率之比为2 ∶ 1

D. 电机所做的功之比为4 ∶ 5

解析：根据位移相同可得两图线与时间围成的面积相等，即■v0 × 2t0 =■×■v0[2t0 + t′ +（t0 + t′）]，解得t′=■t0。则对于第①次和第②次提升过程中，矿车上升所用的时间之比为2t0 ∶（2t0 +■t0）= 4 ∶ 5，则选项A正确;加速过程中的牵引力最大，且已知两次加速时的加速度大小相等，故两次中最大牵引力相等，则选项B错误;由题知两次提升的过程中矿车的最大速度之比为2 ∶ 1，由功率P = Fv可知最大功率之比为2 ∶ 1，则选项C正确;两次提升过程中矿车的初、末速度都为零，则电机所做的功等于克服重力做的功，重力做的功相等，故电机所做的功之比为1 ∶ 1，则选项D错误。

答案：A、C

二、根据题意巧妙建立图像快速解题

【例8】 甲、乙、丙三辆汽车沿直线以相同的速度经过某一路标，从此开始，甲车一直做匀速直线运动，乙车先加速后减速，丙车先减速后加速，它们经过下一个路标时速度相同，则哪一辆汽车先经过下一个路标？

解析：根据题意可知，三辆汽车的初、末速度相同，它们经过的位移相同，而题中并不知乙、丙两汽车在各阶段是否做匀变速直线运动，故只能看做变速直线运动，至此许多同学觉得似乎无法求解。

事实上，采用图像求解本题则非常简单。在同一直角坐标系中，分别作出该三辆汽车的v - t图像，如图9所示。从图像中很容易看出：乙车通过下一个路标所用的时间最短，亦即乙车先通过下一个路标。

【例9】汽车沿平直公路从静止以恒定的加速度启动，最后做匀速直线运动，其速度为vm。从开始到达到速度vm所用时间为t0，求在这段时间内汽车的平均速度与vm的关系。

解析：汽车从静止到达到速度vm的过程中，先做匀加速直线运动，当达到额定功率后，做加速度又逐渐减小、速度逐渐增大的变加速直线运动，因此利用匀变速直线运动的知识无法求出汽车的平均速度与vm的关系。至此，许多同学有一种“山穷水复疑无路”之感。

其实，只要作出汽车的v - t图像，如图12所示。根据图像的物理意义以及求平均速度的公式可知：v>■vm。

【例10】 如图13所示，甲、乙两物体同时由静止从A处出发，沿直线AB运动。甲先以加速度a1做匀加速运动，经过一段时间后，改以加速度a2做匀加速运动，到达B处的速度为v0;乙一直以加速度a做匀加速运动，到达B处的速度也为v0，且a1 > a。则下列叙述中正确的是

A. 甲、乙可能同时到达B处

B. 甲一定先到达B处

C. A、B间的任一点时，甲的速度一定大于乙的速度

D. A、B间的任一点时，甲的速度可能小于乙的速度

解析：本题若直接运用运动学公式来求解，由于涉及的物理量较多，计算过程必然会很繁琐。

若作出这两个物体的v - t图像，利用它们的位移、B处的速度相同，即两斜线区域的面积相等，则很容易得出选项B、C正确，如图13所示。

【例11】小球以初速度v0上抛，已知小球运动过程中受到空气的阻力与其速率成正比，且落回抛点时小球速度为v，求小球从上抛到落回抛点全过程所需的时间。

解析：由于小球所受的阻力与速率成正比，因此无论是在上抛阶段还是下落阶段，小球所受的合外力是变力，加速度为变量，所以无法用匀加速直线运动的公式求解。为此可采用图像法顺利获解。

因为v - t图线与t轴所围的面积表示小球在对应时间内经过的位移大小，而且上抛与下落阶段所经过的位移大小相同，所以图14中区域I与区域II面积相等。由已知条件可知，小球运动过程中受到空气的阻力与其速率成正比。

设阻力f = -kv，據此可画f - t图像，如图15。区域I′与区域II′的面积一定分别是图15中区域I和区域II面积的k倍。由此可知，区域I′与区域II′的面积也相等。

因为冲量I = Ft，所以图15中曲线与t轴所围成的面积表示对应时间内阻力f的冲量值。由此可见，在小球上抛和下落过程中，阻力的冲量等大反向，全过程阻力的合冲量为零。

对全过程运用质点动量定理，设向上为正方向，则有：- mv - mv0 = - mgt + If = - mgt，所以t =■=■，故小球全过程所用的时间t =■。

由上述几例可见，在运动学中善用图像解题，可达到化难为易、避繁就简、快速获解的目的，收到事半功倍的效果。

责任编辑   李平安