基于多目标加权灰靶决策模型的节能服务公司选择研究
2019-03-07张文杰袁红平
张文杰,袁红平
(1.西南交通大学经济管理学院,四川 成都 610031;2.广州大学工商管理学院,广东 广州 510006)
1 引言
节能服务公司(Energy Service Company,ESCO)是合同能源管理(Energy Performance Contracting,EPC)中最主要的利益主体,也决定着节能项目能否顺利推进[1]。目前,国内外学者对ESCO的研究涉及众多方面,Painuly等[2]关注发展中国家ESCO发展初期面临的问题;张冬梅[3]采用博弈论探讨了ESCO与用能单位间的市场行为;刘桦和李晨[4]对国内外建筑行业的ESCO进行了对比研究;Guertler和Smith[5]对ESCO节能收益投资进行研究;Bannai等[6]关注了ESCO业务与电力、燃料价格波动的关系。近期的一些研究指出,选择一个合适的ESCO是EPC项目顺利开展和实施的基础,也是用能方实现利益最大化的最有效途径,ESCO的选择问题正引发越来越多的关注。
作为EPC真正的节能效益享受者,用能方该如何从自己的利益出发,从多个ESCO中选出最有利于自身的ESCO已成为EPC研究的重要话题。而“采用什么样的选择方法来选择ESCO?根据什么样的指标来选择ESCO?”则是ESCO选择中需要首先解决的两大难题。Okey和Akma[7]比较分析了38个不同国家的ESCO指标;Okay等[8]、Stuart等[9]发现“节能保证量(guaranteed savings)”、“信誉(credit)”和“节能分享量(shared savings)”是用能企业衡量ESCO优劣的三大重要指标;杨锋等[10]在基于多属性逆向拍卖模型对节能服务公司(ESCO)选择问题的研究中指出,用能方可以根据“能源节省量”与“项目提前期”来选择最优的ESCO;Bertoldi等[11]、Fang等[12]、Suhonen和Okkonen[13]指出经济性、成本和收益、节能设备安装服务是用能方考评ESCO的重要指标。同时,节能设备和技术、节能方案设计、EPC合同、节能设备可靠性等也是用能方选择ESCO的主要关注点[14]。
上述研究多是提出衡量ESCO的标准[11-14],或者在既定选择标准下进行ESCO选择[10]。然而,在实际项目中,用能方更关注如何在保证自身利益目标的前提下,通过分析少量的、不足的ESCO信息,从多个ESCO中挑选出对自己最为有利的ESCO,现有研究并未能解决这一问题。本文拟从用能方的角度,结合灰色系统理论中的多目标加权灰靶决策模型来探讨ESCO的选择问题。
2 多目标加权灰靶决策的适用性分析
邓聚龙[15]最早提出了灰色系统理论,以灰色系统理论为基础,刘思峰等[16]在基于4种一致性效果测度函数的构造基础上提出了多目标加权灰靶决策模型。多目标加权灰靶决策模型可以帮助决策者在少信息、贫数据情境下,从多个决策目标中选择最优决策目标。与灰靶决策方法相比,多目标加权灰靶决策模型主要具有两方面优势:①增加了权数,充分考虑了实际应用中不同决策目标重要性程度的不同;②充分考虑了目标效果值和目标效果向量中靶和脱靶两种不同情形,大大提高综合效果测度的分辨率[16-17]。
多目标加权灰靶决策模型已被广泛用于解决各类决策目标选择问题。例如:杨耀红和谭攀静[18]将该方法用于供应链供应商选择;代岚等[19]借助此方法解决了应急避难场选址的问题;高旭阔和张晓雪[20]将多目标加权灰靶决策用于既有建筑节能改造方案选择;谢伟和刘宝新[21]利用多目标加权灰靶决策模型进行军事运输方式的选择。此外,此方法还被用于解决煤炭领域[22]、军事装备领域[23]、地质灾害评估领域[24]等的决策目标选择问题。
上述决策目标选择问题的共性表现为:①直接可用的目标决策信息缺乏;②存在多个决策目标;③多个决策目标对于决策的重要性程度不完全相同;④通过比较综合效果测度值来识别最优决策。因此,多目标加权灰靶决策模型非常适合于帮助用能方在贫数据情况下解决需要考虑多个决策目标、且各决策目标重要性程度不同的ESCO选择问题。基于此,本文将首先对多目标加权灰靶决策模型进行简要阐述,并简要列出该模型的主要计算步骤。在此基础上,结合某区政府的算例来对多目标加权灰靶决策模型在ESCO选择问题中的实用性、有效性进行实证。
3 多目标加权灰靶决策模型
基于刘思峰等[16]提出的多目标加权灰靶决策模型,本文列出文献[15-17]中对多目标加权灰靶决策模型相关定义:
定义1:将需要研究、解决的问题或需要处理的事物以及一个系统行为的现状统称为事件,研究范围内的全体事件统称为该研究范围内的事件集,记作A={a1,a2,…,an},
其中ai(i=1,2,3,…,n)为第i个事件;
定义2:将所有可能的对策全体称为对策集,记作B={b1,b2,…,bm},其中
bj(j=1,2,3,…,m)为第j个对策;
定义3:事件集A={a1,a2,…,an}和对策集B={b1,b2,…,bm}的笛卡尔积S=A×B={(ai,bj)|ai∈A,bj∈B(}称为决策方案集,对于任意sij=(ai,bj)称为决策方案;
定义4:



4 多目标加权灰靶决策模型计算步骤
根据文献[16-17],本文列出多目标加权灰靶决策模型的详细步骤,具体如下:
步骤一:将要解决的问题以及相应的对策分别设定为事件集A={a1,a2,…,an}和对策集B={b1,b2,…,bm}在此基础上,构造决策方案集
S={sij=(ai,bj)|ai∈A,bj∈B(};
步骤二:根据实际需求确定决策目标k(k=1,2,…,s);
步骤三:采用AHP法确定各目标的决策权η1,η2,…,ηs;
步骤四:对目标k(k=1,2,…,s)求相应的目标效果样本矩阵;

步骤六:求k目标下一致效果测度矩阵

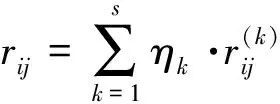
5 算例分析
某区政府打算对一栋行政大楼进行能源系统改造,计划节能改造期限为16个月,容忍限为1个月,现已初步筛选出三家节能服务公司(ESCO)。根据该区政府的要求,3家ESCO(ESCO1;ESCO2;ESCO3)分别提供了各自公司的自评报告和该项目节能改造数据。本文以多目标加权灰靶决策评估模型为基础,对3家ESCO提供的数据资料进行综合分析后,得出该区政府应该与ESCO1进行下一步谈判、协商签订节能服务合同的决策。整个决策过程如下:
步骤一:建立事件集、对策集及决策方案集。
将选择哪家ESCO进行下一步谈判、协商作为事件a1,则事件A={ai}={a1};将选择ESCO1、ESCO2、ESCO3分别作为对策b1,b2,b3,则对策集B={bj}={b1,b2,b3};由事件集A和对策集B构造决策方案集
S={sij=(ai,bj)|ai∈A,bj∈B(}={s11,s12,s13}。
步骤二:确定决策目标
采用专家咨询法,经过2轮专家咨询后确定了“公司资质状况”、“公司信誉状况”、“节能设备质量”、“节能改造期”、“节能效益分享期”、“节能设计方案”、“参与节能效益分享比例”、“节能改造对原建筑的破坏程度”、“合同期年保证节能量”、“节能量检测难易程度”、“先期预付款”等11个方面作为3家ESCO的决策目标。经过论证,确定了该11个决策目标的类型,具体如表1所示:

表1 ESCO决策目标统计表
*注:效益型目标:是指效果样本值越大越好;成本型目标:是指效果样本值越小越好;适中型目标:是指效果样本值越接近某一适中值越好。
步骤三:确定11个决策目标的决策权数。采用层次分析法(Analytic Hierarchy Process, AHP)对11个决策目标的决策权重系数进行确定,最终各决策目标的决策权数如表2所示:

表2 目标决策权统计表
步骤四:求各目标的效果样本向量
对表1中备注为“定性”的决策目标进行专家评分,将其转化为定量指标。所有6个定性指标的评分均采用10分值,“10分”代表最优、最好、最大、最困难,“0分”代表最劣、最差、最小、最容易。各决策目标的分值采用算数平均法,在对各8位专家评分进行加总平均后求得。根据3家ESCO所提供的自评报告以及所提供的该项目节能改造数据,研究对表1中备注为“定量”的决策目标进行汇总,整理后形成表3:
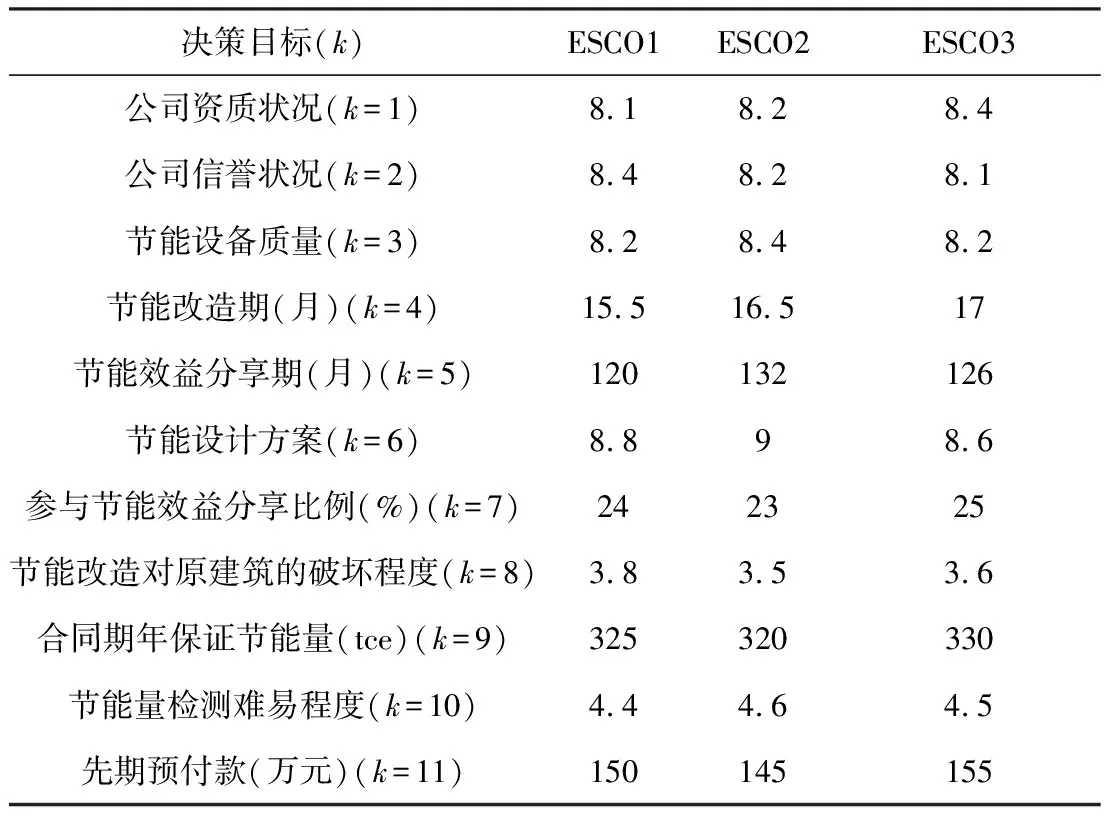
表3 目标效果统计表
根据表3形成目标效果样本矩阵:




步骤六:求k目标下一致效果测度矩阵
本步骤主要是为本研究中所涉及的11项不同量纲的决策目标去量纲化,结合步骤五设定的目标效果临界值矩阵,以及文献[13-15]相关计算理论,对效果样本矩阵U(k)进行k目标下一致效果测度矩阵计算。计算主要遵循以下法则:
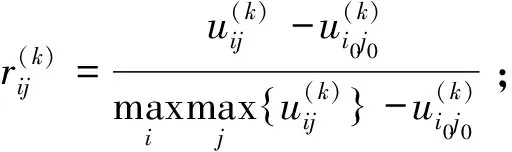
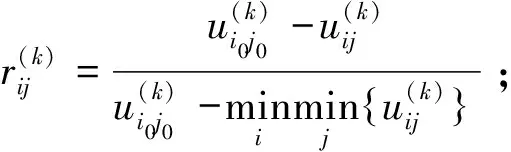
法则3:设k=4时为适中型目标,即目标效果样本值越接近适中值A(可知A=16)越好,其中:
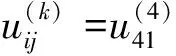

步骤6-1:当k=1时:k目标下一致效果测度矩阵计算遵循法则1,即:
按照此法则(法则1),分别求出k=2,3,6,9时的一致效果测度矩阵。
步骤6-2:当k=5时:k目标下一致效果测度矩阵计算遵循法则2,即:
按照此法则(法则2),分别求出k=7,8,10,11时的一致效果测度矩阵。
步骤6-3:当k=4时:k目标下一致效果测度矩阵计算遵循法则3,分两种情况考虑:

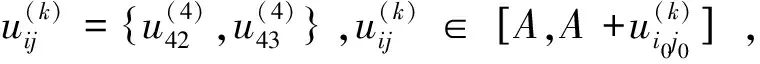
步骤6-4:将所有k目标下一致效果测度函数值汇总,形成k目标下一致效果测度矩阵Rk,即:
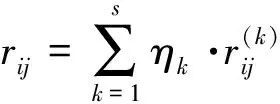
由表2可得k目标下的决策权矩阵
则综合效果测度矩阵
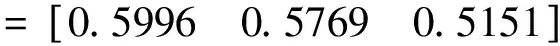
步骤八:确定最优对策bj0
由r11=0.5996,r12=0.5769,r13=0.5151,即:r11,r12,r13均大于0,可知该三家ESCO均中灰靶,表明筛选的这三家ESCO进行最终决策是合理的。
观察三家ESCO各自的综合效果测度值,可以发现三个综合效果测度值均介于0.5至0.6之间,差值相对较小。造成这一结果的原因可能是三家备选ESCO本身在综合考评的11项优选指标方面差距并不是特别显著,因此,无法直观地识别出绝对优势方案,但是,借助本文所构建的多目标加权灰靶决策模型可以较有效的实现定量化方案优选。
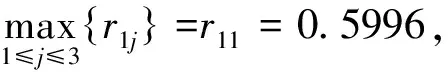
6 结语
本文的主要研究结论为:
(1)在对ESCO进行优选时,应着重关注“公司资质状况”、“公司信誉状况”、“节能设备质量”、“节能改造期”、“节能效益分享期”、“节能设计方案”、“参与节能效益分享比例”、“节能改造对原建筑的破坏程度”、“合同期年保证节能量”、“节能量检测难易程度”、“先期预付款”等11个方面。
(2)将多目标加权灰靶决策模型应用于ESCO选择中,可有效帮助用能方解决在少数据、数据不全情况下的ESCO选择问题,使选择结果更科学、更合理。
(3)实证算例结果表明,运用多目标加权灰靶决策模型计算出的三家ESCO的综合效果测度值中ESCO1的值最大,表明ESCO1最接近灰靶靶心,该区政府应该选择ESCO1。最终核实结果也表明,该区政府也在多方讨论后最终选择与ESCO1进行第二轮谈判,与本文的分析结果吻合。因此,本文所构建的多目标加权灰靶决策模型具有较强的适用性。
附录:AHP法计算出的各级指标权重
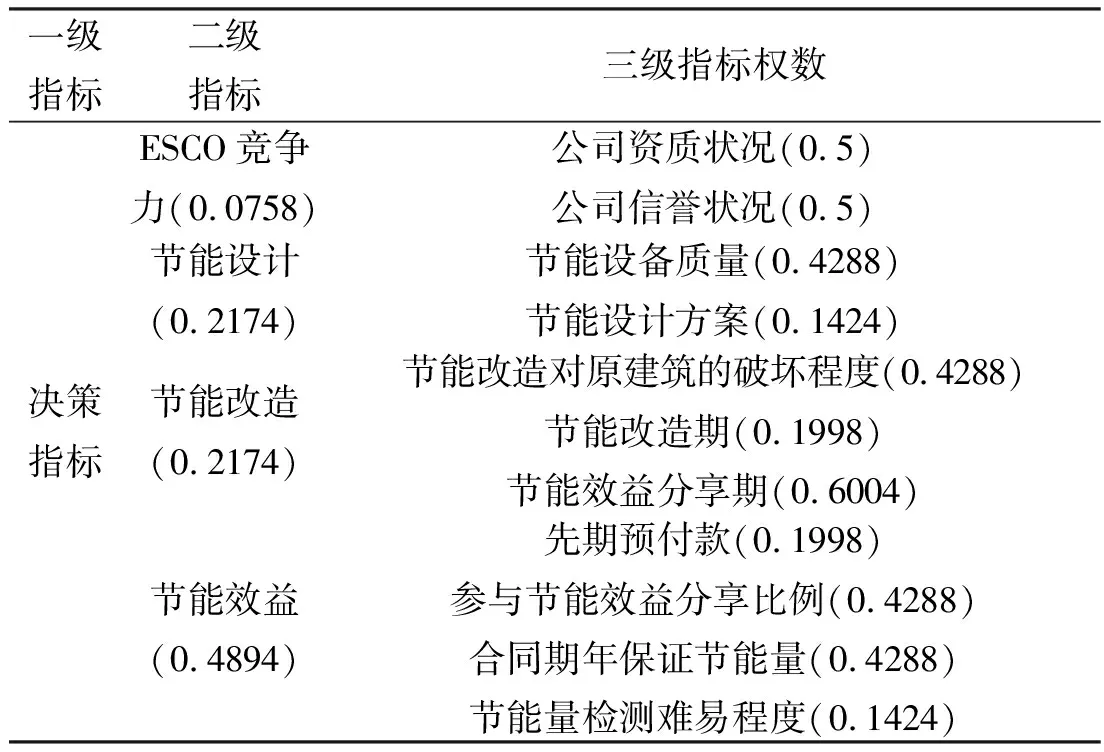
一级指标二级指标三级指标权数决策指标ESCO竞争力(0.0758)公司资质状况(0.5)公司信誉状况(0.5)节能设计(0.2174)节能设备质量(0.4288)节能设计方案(0.1424)节能改造(0.2174)节能改造对原建筑的破坏程度(0.4288)节能改造期(0.1998)节能效益分享期(0.6004)节能效益(0.4894)先期预付款(0.1998)参与节能效益分享比例(0.4288)合同期年保证节能量(0.4288)节能量检测难易程度(0.1424)
