原木材积求算方法的研究

宋新卫，周传统，阴淑文，倪 静

（1.肥城市新城街道办事处林果站，山东 泰安271600；2.肥城市林业局）

在生产实际工作中，原木的材积是由《原木材积表》查表计算，目前执行GB4814—1984标准，本标准适用于所有材种的原木材积计算。当小径4—12cm 的原木材积由公式V＝0.7854L（D＋0.45L＋0.2）2÷10000确定；当小径14cm以上的原木材积由公式V＝0.7854L[D＋0.5L＋0.005L2＋0.000125L（14－L）2（D－10）]2÷10000确定；当检尺长度低于2m或大于10m其材积由公式 V＝0.8L（D＋0.5L）2÷10000 确定。 以上三式中 V—材积（m3）；L—检尺长（m）；D—小径（cm）。由于原木的形状会因树种、地域环境、经营培育目的、品种以及原木树干不同部位等因素的影响，其树干曲线形状会有一定的差异。因此，所有原木用同一个材积表求算的材积不一定符合实际。为了更好的求算原木材积，结合《测树学》的关于原木纵断面形状“近似抛物线”的论述及数学关于抛物线体的有关计算公式，总结了一种原木材积的求算方法论述如下，供参考。

1 计算原木大头直径

由《测树学》的有关论述可知，原木的纵断面形状近似抛物线，因此，原木的材积可以用抛物线体的体积公式：

根据《原木材积表》由以上公式（1），可以推出原木的大头直径理论数值计算公式：

以上计算公式（1）、（2），V—原木材积（m3）；R—大头半径 （cm）；r—小头半径 （cm）；D—大头直径（cm）；d—小径（cm）；L—检尺长（m）；π—圆周率。

2 原木实际材积的计算方法

由“1计算原木大头直径”的论述，根据上述公式（1），可以推出原木的实际材积：

以上计算公式（3），V实际—实际材积（m3）；V—原木材积 （m3）；D实际—实际量测的大头直径（cm）；D—由公式（2）求算的大头直径（cm）；d—小径（cm）。

3 以例说明

根据“2原木实际材积的计算方法”的论述，以原木检尺长为2.6m为例，做进一步实例论述。

3.1 实际量测原木大头直径（D实际）比用公式（2）求算原木的大头直径（D）减少10%时

当小径分别为4cm、6cm、8cm.........时，根据公式（2）计算原木大头直径理论数值过程如下：

由以上计算可知，小径分别为 4cm、6cm、8cm........时，结合公式（2）计算结果大头直径分别为6.5cm、8.5cm、10.6cm.........等，如果实际量测原木大头直径（D实际）减少10%时计算结果如下：

D实际4=6.5×（100%－10%）=5.9cm

D实际6=8.5×（100%－10%）=7.7cm

D实际8=10.6×（100%－10%）=9.5cm

根据公式（3）计算当实际量测原木大头直径（D实际）减少10%时的原木材积计算结果如下：

3.2 实际量测原木大头直径（D实际）比用公式（2）求算原木的大头直径（D）增加10%时

小径分别为4cm、6cm、8cm.........时，结合公式（2） 计 算 结 果 大 头 直 径 分 别 为 6.5cm、8.5cm、10.6cm.........等，如果实际量测原木大头直径（D实际）增加10%时计算结果如下：

D实际4=6.5×（100%＋10%）=7.2cm

D实际6=8.5×（100%＋10%）=9.4cm

D实际8=10.6×（100%＋10%）=11.7cm

根据公式（3）计算当实际量测原木大头直径（D实际）增加10%时的原木材积计算结果如下：

以此类推，可以计算出其它规格的原木，详见表1：长度2.6m原木计算表。

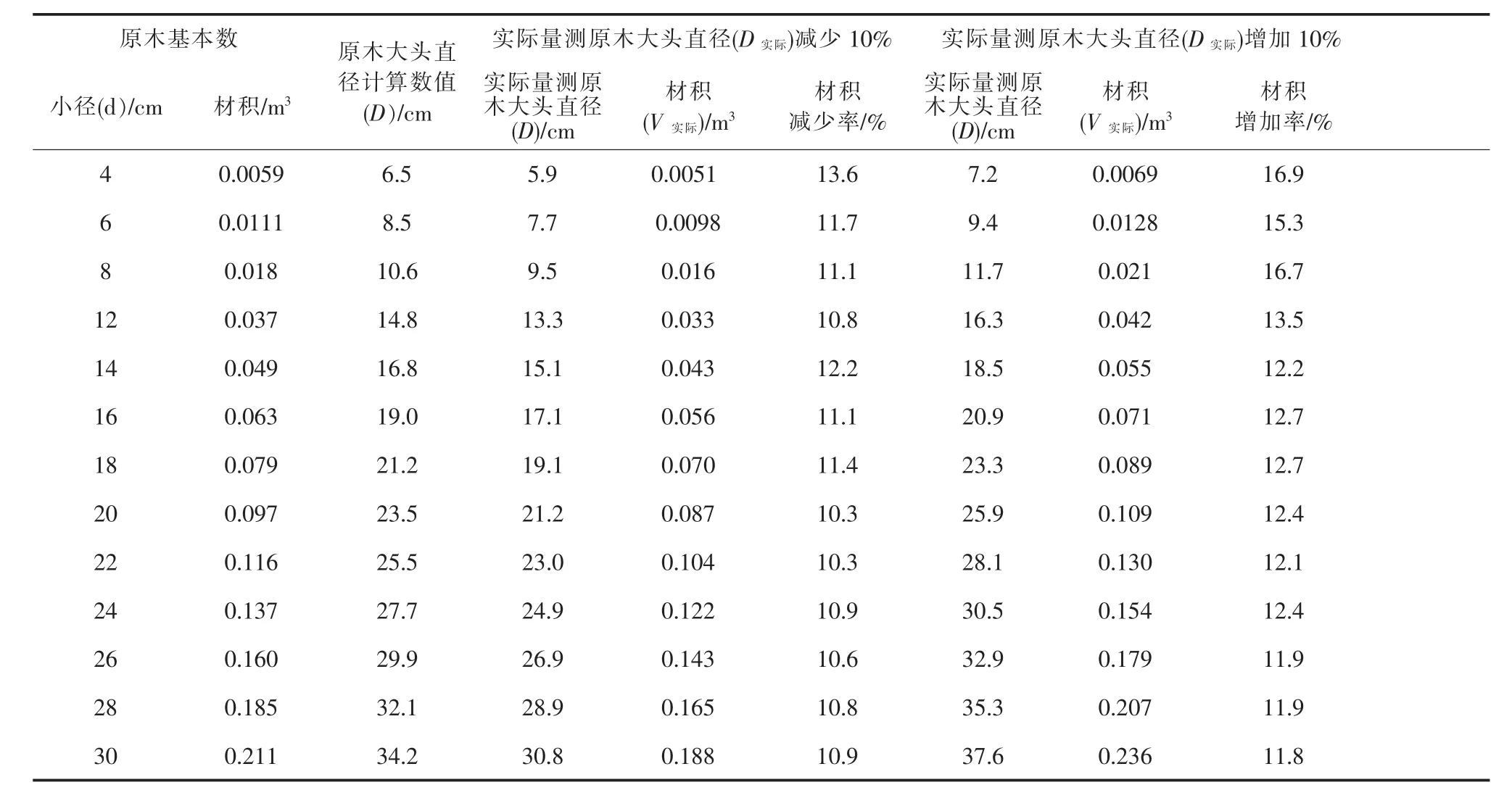
表1 长度2.6m原木计算表

4 结论

这种求算原木材积的方法，由于考虑到了同一小径原木大头直径的差异，这样求算的原木材积将会更加接近实际。因此，应用此方法在实际工作中可以更为精确地求算出不同原木的材积，但由于原木的纵断面形状是“近似抛物线”，此方法仍存有误差。因此，更简单、更便捷、更科学的方法还需继续研究探讨应用。