基于相关性分析的SAR图像目标方位角估计
2019-03-06段芃芃
段芃芃, 刘 锂
(成都理工大学工程技术学院, 四川 乐山 614000)
0 引 言
合成孔径雷达(synthetic aperture radar,SAR)图像具有很强的方位角敏感性,即目标特性随着方位角变化会发生较为剧烈的改变[1]。由此,SAR目标方位角估计可以为SAR目标识别提供有效的先验信息从而缩小搜索空间,提高目标识别性能[2-4]。现有的SAR目标方位角方法主要分为两类。一类是基于目标二值区域的估计算法[5-10]。这是目前采用的最多的方位角估计方法。该方法首先采用目标分割的方法获取目标的二值区域,进而对其进行分析得到目标方位角的估计值。代表性的方法有惯性矩法[5]、主导边界法[5-8]和主轴法[5,9,10]等。另一类方法则是通过考察待估计样本与训练样本的相关性估计方位角[11-12]。文献[11]采用稀疏表示的方法得到能够最优重构待估计样本的训练样本从而得到方位角估计值。对比而言,基于目标二值区域的方法独立于训练样本,无需训练过程。然而,这类方法对于目标分割性能有着较为严格的要求,即目标分割的精度对最终的方位角估计有着重要影响。同时,由于地面目标自身在物理结构上通常具有对称性,因此这类方法难以克服180°模糊问题,即估计的方位角可能是真实方位角的180°对称角度。目前基于稀疏表示的方位角估计方法根据能够最优重构待估计样本的训练样本来估计方位角。这种采用单个训练样本的方法稳健性较差,很容易因为求解的不稳定或者对应方位角样本的缺失导致估计结果的失准。
本文提出基于相关分析的方位角估计算法。由于SAR图像方位角的敏感性,具有相近方位角的SAR图像呈现较高的相关。同时,考虑SAR图像的180°模糊问题,测试样本与训练样本的相关系数呈现双峰值特性。根据这一特点,本文综合分析各类相关系数中的峰值位置,并根据对应的相关系数大小加权得到最终的方位角估计值。本文提出的基于相关分析的算法避免了复杂的SAR图像目标分割,因此效率较高。相比基于稀疏表示的方法,本方法综合考虑了相关系数在各类训练样本中的分布,从而具有更强的稳健性。为了验证本文方法的有效性,采用MSTAR(Moving and Stationary Target Acquisition and Recognition)数据集进行了方位角估计实验。
1 图像相关
图像相关是评价图像相似性的一种简单有效的度量准则[13]。对于两幅图像f和g,其相关系数的计算方法如下式所示。
r(m,n)=
(1)
公式(1)计算了在图像的x,y的两个方向不同偏置(m,n)下的相关系数。根据相关定理[13],图像域的相关操作可以转换为频域的乘积运算,从而可以快速求得相关系数矩阵。通常采用相关系数矩阵的最大值作为两幅图像之间的相关,如公式(2)所示。
R=max(r(m,n))
(2)
2 方位角估计
由于SAR图像的方位角敏感性,待估计样本仅仅与其具有相近方位角的样本保持较高的相关性。这体现在两个方面:(1)同类目标中,具有相近方位角的样本之间体现很高的相关,当方位角差距较大时,相关明显减弱;(2)不同类中,具有相近方位角的样本体现较高的相关,当方位角差距较大时,相关显著减弱。由于180°模糊问题,这种相关特性呈现180°对称性。由此,待估计样本与各类目标训练样本的相关系数呈现双峰值得分布特点,即接近真实方位角处以及180°对称处。同时,在接近真实方位角的位置体现较高的相似性。图1(a)显示一幅真实方位角为76.5°的BMP2 SAR图像在BMP2,BTR70和T72 3类目标训练样本集上的相关系数分布。具体相关系数曲线分别如图1(b),(c),(d))所示。可以看出,在任一类上的相关系数均表现出双峰值的特性,并且峰值的位置呈180°对称。同时,在真实目标类别(即BMP2)的峰值处表现出更高的相关系数。据此,本文进行方位角估计实施步骤如下:
(1)根据公式(1),(2)计算待估计样本与C类训练样本的相关系数曲线;
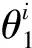
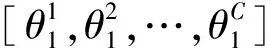
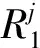
(3)
(5)按照公式(4)通过线性加权得到估计的方位角。
(4)
由此可见,本文的方位角估计算法充分利用了待估计样本与各类训练样本的相关性,通过相关性的分布规律得到更为稳健的估计值。通过相关系数的大小分析,有效克服了传统算法中的180°模糊问题。采用本文提出的方位角算法对图中的BMP2图像估计得到的方位角为77.3°,与真实方位角的误差大小为0.8°。可见,本文提出的算法可以以较高的精度得完成了方位角估计任务。
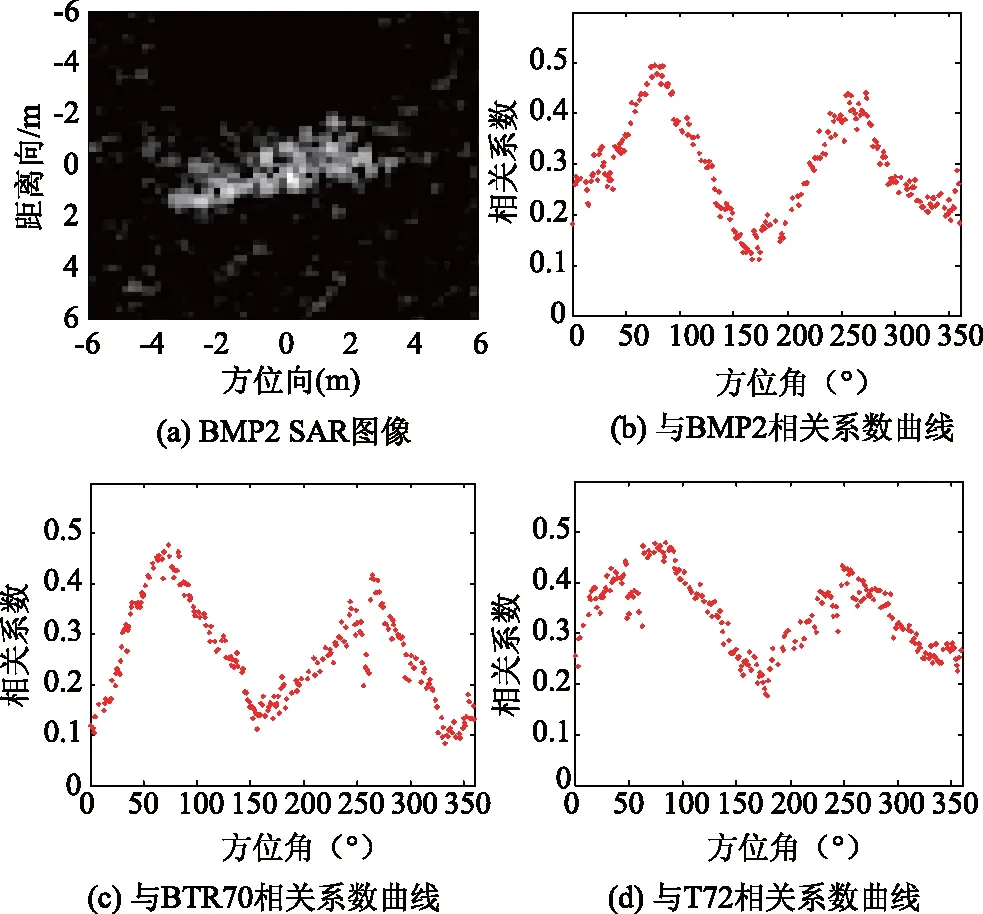
图1 一幅BMP 2SAR图像与各类训练样本的 相关系数曲线
3 实验与分析
3.1 实验数据集
采用MSTAR数据集中3类目标7个型号的SAR图像进行方位角估计实验。图2给出了3类目标的光学图像。表1列出了本文使用的训练样本和测试样本。实验中采用俯仰角17°下的3类目标图像作为训练样本,俯仰角15°下的3类目标图像作为待估计的测试图像。训练和测试样本的方位角真值均可从MSTAR数据的文件头中读出。

图2 3类目标的光学图像
3.2 实验结果与分析
采用本文提出的算法对3类目标的测试样本进行方位角估计。表2以估计误差在±10°以内为准则判定为正确估计,超出范围则认为是错误估计。可以看出,本文方法对于99%以上的测试图像都可以达到正确的估计,充分表明了本文方法的有效性。表3进一步分析了提出算法的方位角估计性能,3类目标的方位角估计精度较为接近。总体上,1365个测试样本中有1334个(95.38%)的估计误差都在5°以内。图3显示了本文方法的误差分布图,可以看出绝大多数测试样本的估计误差均在2°以内,充分证明了提出方法的估计精度较高。
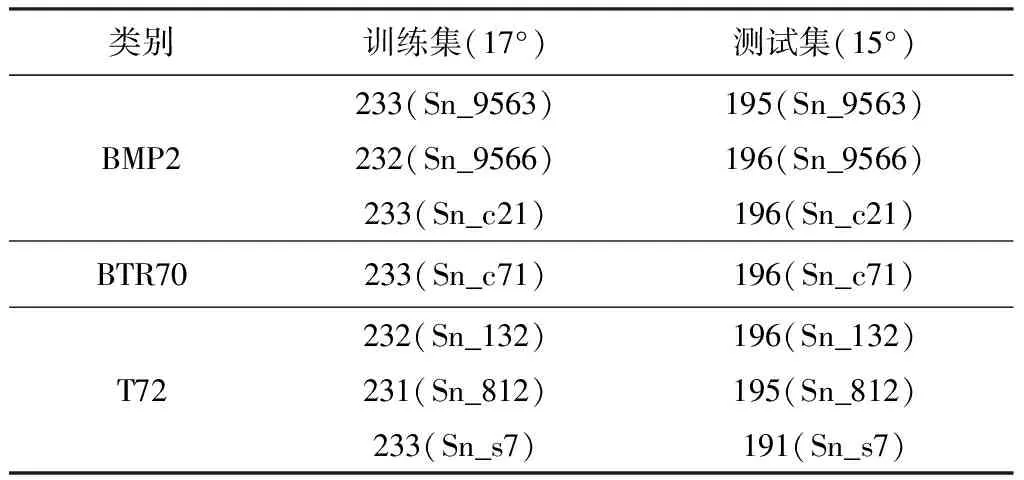
表1 训练集和测试集
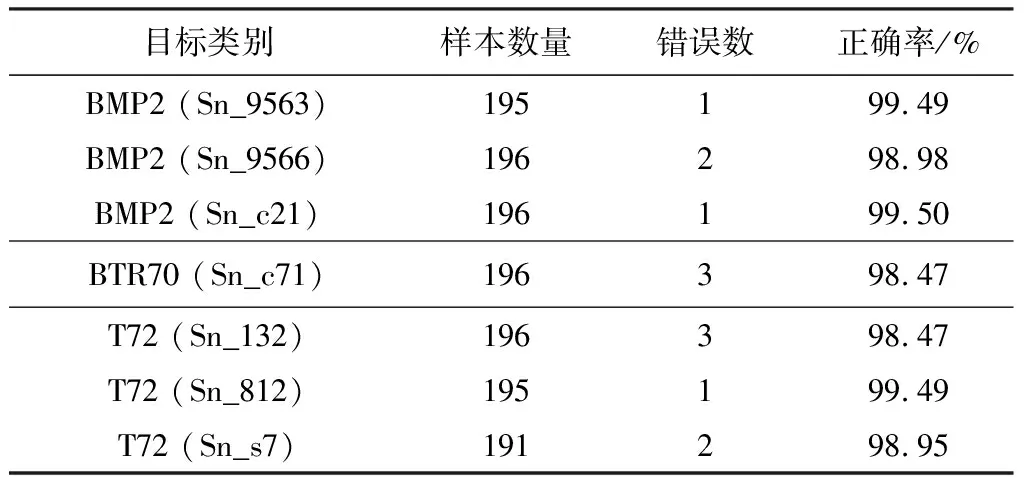
表2 本文方法的方位角估计结果统计
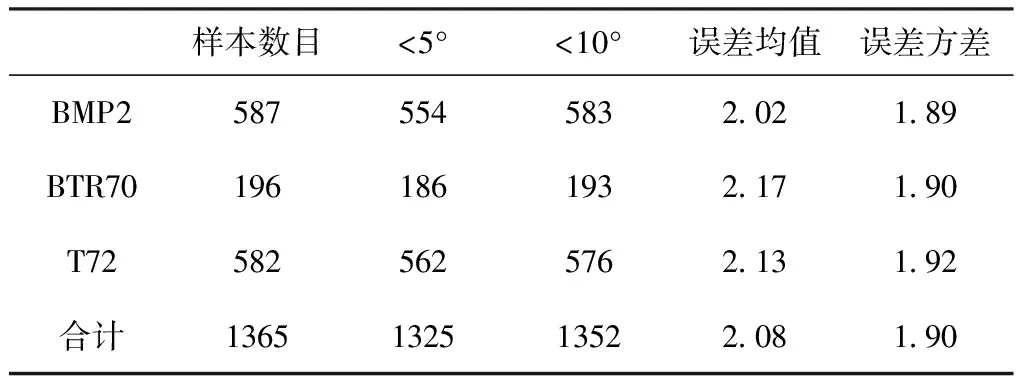
表3 本文方法的估计精度
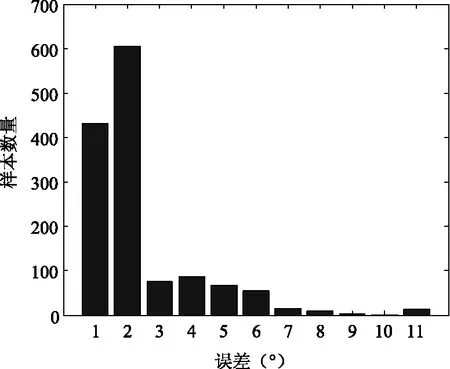
图3 本文方法的估计误差分布
表4对比了本文方法与几类经典的方位角估计方法的性能。本文方法的性能显著优于传统基于目标二值区域的最小外接矩形法[4]、主导边界法[5]。此外,本文方法可以避免复杂的SAR目标分割并且可以克服传统方法中的180°模糊问题。对比本文方法和文献[10]中的稀疏表示方法,本文的方法的性能更好。尤其是在估计精度要求高的情况下(如估计误差小于2°),本文方法的优势更为明显。由于本文方法充分考虑了待估计样本与各类训练样本的相关性,并通过线性加权的方法综合各个类别中获取的有益信息,因此相比基于稀疏表示方法中单个样本估计的手段更为稳健。表5对比不同方法在同一计算平台上估计单个测试样本所需要的时间消耗,可以看出本文算法的效率最高。基于目标二值区域的方法的主要时间消耗发生在目标区域的提取上。相比求解稀疏表示系数,本文的线性相关系数的计算更为简便。具体而言,对于规模为n的训练集,本文方法的复杂度为O(n)而基于稀疏表示的方法的复杂度O(kn)(其中k代表稀疏度)。这些实验结果均证明了本文算法对于SAR图像目标方位角的估计具有更高的效率、精度以及更强的稳健性。
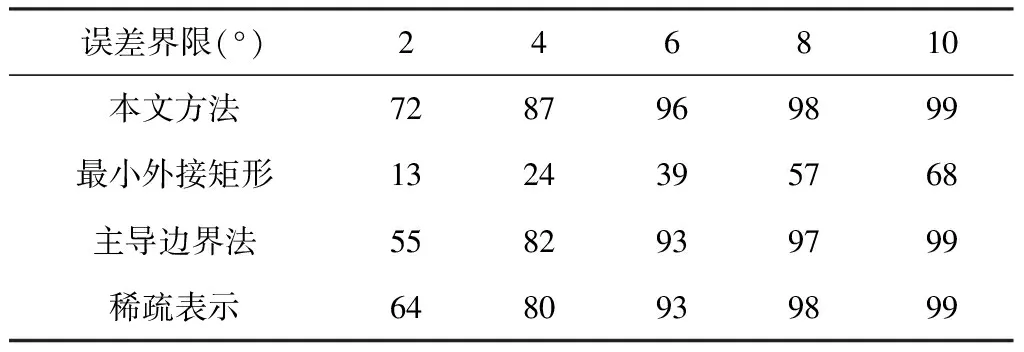
表4 方位角估计绝对误差在指定范围内的百分比(%)

表5 不同方法的时间消耗
4 结 语
本文提出基于相关分析的SAR目标方位角估计方法。该方法通过分析待估计图像与各类训练样本的相关系数分布规律,高效、稳健地估计出其方位角。相比基于二值区域的方位角估计算法,本文方法避免了复杂的目标分割过程,从而具有更高的效率。相比基于稀疏表示的方法,本文方法充分利用各个类别的所有训练样本,大大提高了方位角估计的稳健性。采用3类MSTAR数据进行了方位角估计实验,本文算法具有很高的方位角估计效率和精度并且可以很好地克服传统算法中180°模糊问题,这些结果均证明了本文方法的优越性。
