最大化有向传感网络寿命的目标覆盖算法

喻 林，朱晓珺

(1.郑州财税金融职业学院 信息技术系，河南 郑州 450048；2.郑州信息科技职业学院 信息工程学院,河南 郑州 450000)

0 引 言

有向传感网络(Directional Sensor Networks, DSNs )就是利用传感节点感知的有向性建立的无线网络[1-3]。在DSNs中，传感节点有方向性地感测环境数据，并将数据传输至信宿(Sink)。与全向(Omni-directional)传感节点不同，有向传感节点具有方向性，并且每个方向的感测区域呈扇形状。DSNs通过传感节点感测的有向性，提高了通信资源的使用率，并降低了对其他网络的干扰，也满足了不同目标覆盖的差异怀。目前，DSNs已广泛应用于各类监测领域。这些应用的关键在于如何有效地对覆盖目标进行覆盖，即目标覆盖控制问题。

近期，研究人员对DSNs的覆盖控制进行大量的研究工作。所谓覆盖控制就是以尽量少的传感节点数实现区域的最大覆盖[4]。然而，文献[5-6]已证实，覆盖控制是NP问题，只能获取次优解[7]。因此，覆盖问题成为DSNs复杂问题之一，其主要涉及传感节点工作时间的选择以及它们感知方向(Sensing sectors)的决策，进而延长网络寿命。

目标覆盖是DSNs的基础，已成为DSNs的研究热点。不同的目标可能具有不同的重要性，因此，它们的覆盖要求不尽相同。例如，智能交通系统(Intelligent Transportation System, ITS)中的交叉路口的流量监控覆盖，相比其他监控覆盖点，具有高的覆盖要求。高性能的监控覆盖性能取决于二值扇形模型。所谓扇形模型是指：如果目标在传感节点的感测覆盖区域内，就认为目标被传感节点覆盖[7-8]。文献[7-8]中，作者提出了不同的算法解决目标覆盖问题，但是它们是假定所有目标具有相同的覆盖重要性。此外，文献[9-11]利用基于Voronoi单元划分，优化活动节点，进而提高覆盖性能。

然而，这些算法均是采用二值扇形模型。但是，对于给定目标，传感节点的感测质量完全取决于它们之间的距离和信号衰减率[12-13]。在文献[12]中， 利用关于传感节点离目标间的距离函数，对覆盖目标质量进行量化，并将网络内所有节点划分多个不相交覆盖集，致使每个覆盖集能满足目标的覆盖要求。同时，引用最大网络寿命分配(Maximal Network Lifetime Scheduling, MNLS)算法，优化覆盖集的工作时间，进而最大化网络寿命。类似地，文献[13]提出面向目标可靠性的有向覆盖集(Directional Cover-set Considering Coverage Reliability, DCCR)算法。DCCR算法利用信号衰减因子建立目标覆盖质量，并通过优化不相交覆盖集，最大化网络寿命，同时满足所有目标的覆盖要求。

然而，在真实环境中，目标检测存在不准确性和异构性，并且多数目标服从概率模型[14]。如果不联合考虑节点的剩余能量和覆盖质量，则很难提高网络寿命。原因在于：不同传感节点的能量消耗率存在较大的差异性。此外，如何分配覆盖集的工作时间，对网络寿命有直接的影响。

为此，本文提出覆盖质量感知的最大化网络寿命(Coverage Quality aware-based Network Lifetime Maximization，CQ-NLM)算法，提高覆盖质量和网络寿命。CQ-NLM算法的主要目的就是以最小的活动节点数最大化覆盖质量，并且这些活动节点数能满足异构覆盖质量。实验数据表明，提出的CQ-NLM算法能够有效地提高网络寿命。

1 系统模型及假设

假定在监测区域内有N个传感节点，且它们随机分布于区域Ω内。这些传感节点实时地感测环境数据，并将数据传输至信宿。一旦部署了，这些传感节点不再移动，即属于静态节点。此外，考虑同构网络，节点具有相同的感测半径Rs和初始能量E0。此外，传感节点具有活动和休眠两种状态，并且能自行切换。

DSNs中每个传感节点有感测和通信功能：

图1 有向传感节点模型

(2)每个传感节点的通信半径为Rc，且Rc≥2Rs[15]。通信的角度为θc，0≤θc≤2π。

此外，假定网络内存在M个目标，且它们的位置已知。N个传感节点随机分布于监测区域，并通过高密度部署，获取高的覆盖率。每个目标具有预定的覆盖质量，且表示为γ(mk)，其中mk表示第k个目标。

2 CQ-NLM算法

CQ-NLM算法目的就是使用最少的传感节点数获取高的覆盖质量。为此，CQ-NLM算法利用混合整数线性规划(Mixed Integer Linear Programming，MILP)建立目标函数[16]。然后，由目标函数建立候选集，并由候选集节点覆盖目标。一旦候选集的寿命耗尽，信宿再选择新的候选集。此外，本文引用如表1所示的标识符。

表1 标识符

2.1 标的覆盖质量

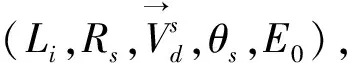
为了判断在传感节点ni的sth扇区内是否存在目标mk，使用TIS算法[5]。如果目标mk离传感节点ni的距离小于Rs，并且在其感知扇区内，则将传感节点ni的sth扇区纳入ξmk，如式(1)所示：

ξmk←di,s, ifD(ni,mk)≤Rs

(1)

其中D(ni,mk)表示传感节点ni离目标mk的欧式距离。

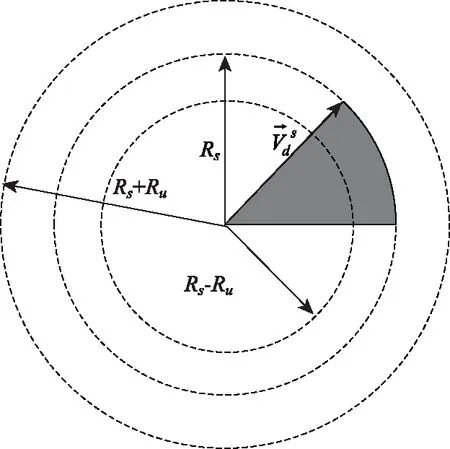
图2 目标的概率覆盖

利用文献[14]所示的概率覆盖模型，可将由传感节点ni的sth扇区所覆盖目标的覆盖质量σi,s(mk)表示如式(2)所示：

(2)

其中Ru表示感测误差。而α=D(ni,mk)-(Rs-Ru)。λ、β分别参数，用于测量检测概率。

引入变量χ，其表示传感节点集，集内的节点感知扇区能够覆盖目标mk。假定有p个传感节点的感知扇形能覆盖目标，则χ={ni|i=1,2,3,…,p}。

因此，累加覆盖目标mk的覆盖质量ρ(mk)如式(3)所示：

(3)

2.2 目标函数

首先建立候选集ψ，其为传感节点的感知扇区η的子集，即ψ⊆η。候选集ψ内节点能够覆盖目标，并且满足每个目标mk的覆盖要求γ(mk)。

然后，再计算候选集ψ的寿命。本文从节点能量定义候选集ψ寿命。如果传感节点ni的初始能量为E0，剩余能量为Er(i)，并且能量消耗率为δ(i)，则传感节点ni的剩余寿命为：

(4)

依据式(4)，可得候选集ψ的寿命τ，如式(5)所示：

τ=min{ζi|di,s∈ψ}

(5)

从式(5)可知，候选集ψ的寿命等于集内节点的最小寿命。

在建立目标函数之前，先引入二值变量bi,s，其值反应了传感节点ni的扇区di,s是否在候选集ψ内。

(6)

CQ-NLM算法的目的就是以最少的传感节点实现覆盖目标的最大化。为此，就是寻找最小的候选集ψ，进而满足覆盖要求。利用MILP所建立的目标函数如式(7)所示：

(7)

那式(7)的约束条件如式(8)～式(11)所示：

∀di,s∈ψ,ψ⊆η

(8)

式(8)确保了在特定候选集内每个节点只有某一个扇区是活动状态，其他扇区是休眠的，这有利于网络寿命的提高。

ρ(mk)≥γ(mk), ∀mk∈M,1≤k≤|M|

(9)

式(9)保证了每个目标都被覆盖，并满足覆盖要求。即有足够的节点最监控目标。

∀mk∈M,1≤k≤|M|

(10)

式(10)保证了满足每个目标的覆盖要求。即每个目标的覆盖质量大于或等于目标预定的覆盖质量。

Er(i)≥Eth,di,s∈ψ,ψ⊆η

(11)

式(11)保证：仅当节点的剩余能量大于能量阈值Eth，该节点才能加入候选集ψ。

对于能量阈值，采用局部均值算法求解能量阈值。将每个扇区内所有节点的平均剩余能量作为能量阈值。当然，计算扇区内节点平均剩余能量存在一定的计算量和通信量，这必然会引起额外的能耗，但这一定是小于本算法所节省的能量，总体仍能够提高能量效率，最终延长网络寿命。后续的实验数据可证实。

依据这些上述约束条件，通过求解目标函数，实现覆盖目标最大化，并延长网络寿命。

3 系统仿真及性能分析

3.1 仿真环境及性能指标

为了更好地分析CQ-NLM算法性能，利用离散事件仿真器NS-3建立仿真平台。有向传感节点和目标均匀地分布于160×160 m2区域。每个节点的初始能量为E0=6 J。预定的覆盖质量ρ从0.1至0.9变化。其他的仿真参数如下：ω=4、λ=1、β=0.5、Rs=50 m、Ru=25 m。仿真时间为1000 s，每次仿真独立重要50次，取平均值作为最终的仿真数据。

选用覆盖率和网络寿命作为评估算法的性能指标。覆盖率等于覆盖面积占总体面积的比率。覆盖率越高，表明DSN网络性能越优。网络寿命表示从部署传感节点开始至DSN内第一个节点失效的时间差。

为了更好地分析CQ-NLM算法的性能，选择同类的MNLS[12]和DCCR[13]作为参照。主要分析它们的覆盖率、网络寿命以及活动传感节点数。其中覆盖率等于覆盖面积占总体面积的比率，覆盖率越高，算法性能越好。而网络寿命是指从网络部署开始至第一个传感节点失效的时间差。

3.2 仿真结果及分析

首先分析传感节点数对网络寿命和活动节点数的影响。目标数M=25，传感节点数从55至80变化，仿真数据如图3所示。

从图3(a)可知，网络寿命随传感节点数的增加而上升。这主要是因为传感节点数的增加，增加网络的总体能量，进而延长了网络寿命。与MNLS和DCCR相比，CQ-NLM算法的网络寿命得到有效提高。原因在于：这主要是因为：MNLS和DCCR并没有优化活动节点数。同时，在选择传感节点数，忽略了覆盖集的剩余能量。而CQ-NLM算法考虑了节点剩余能量，进而延长了网络寿命。与MNLS和DCCR相比，CQ-NLM算法的网络寿命平均延长低于10秒。原因在于：CQ-NLM算法计算能量阈值也需要消耗能量，降低了一定的网络寿命。

图3(b)显示了各算法的活动节点 数。由于CQ-NLM算法通过混合整数线性规划，降低了传感节点数。因此，活动节点数的百分比小于DCCR和MNLS。

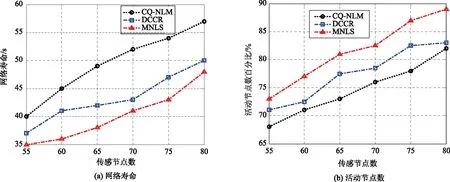
图3 传感节点数对网络寿命和活动节点数的影响

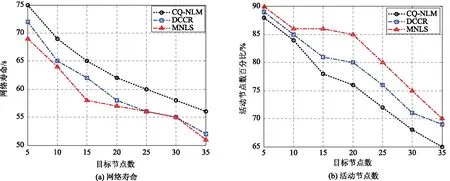
图4 传感节点数对网络寿命和活动节点数的影响(N=80)

然后 分析目标数对网络寿命的影响，其中传感节点数N=80，目标数从5至35变化，仿真数据如图4所示。

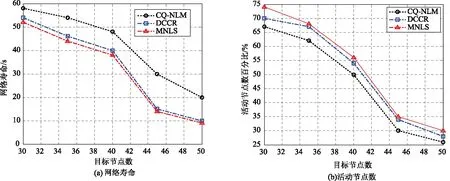
图5 传感节点数对网络寿命和活动节点数的影响(N=50)

从图4(a)可知，随着目标数的增加，网络寿命逐渐下降。原因在于：目标数越多，需要越多的活动传感节点去覆盖目标，进而缩短了网络寿命。与MNLS和DCCR相比，CQ-NLM算法的网络寿命得有效地提高。图4(b)具有与图3(b)类似数据，由于CQ-NLM算法减少了传感节点数量，降低了活动节点数。

再分析恶劣环境：目标数多而传感节点数相对较少的情况。在本次实验中，目标数从30至50变化，传感节点数为50，实验数据如图5所示。

从图5(a)可知，当节点数为50时，目标数的增加，导致网络寿命的急剧下降，原因在于：目标数越多，需要更多的传感节点覆盖目标。而传感节点数一定，这就需要更多的传感节点参与目标覆盖，加大传感的工作时间，进而增加了传感节点的能耗，进而降低了网络寿命。而图5(b)的数据进一步说明目标数的增加，导致更多的节点因能量消耗殆尽而无效，因此，活动节点数减少。特别是当目标数增加到40后，活动节点数急剧下降。

最后，分析节点部署方式对网络寿命的影响。在实验中，考虑均匀部署和随机部署两种方式。具体而言，在160×160m2区域内以均匀和随机部署80个传感节点，目标数从5至35变化。实验数据如图6所示。

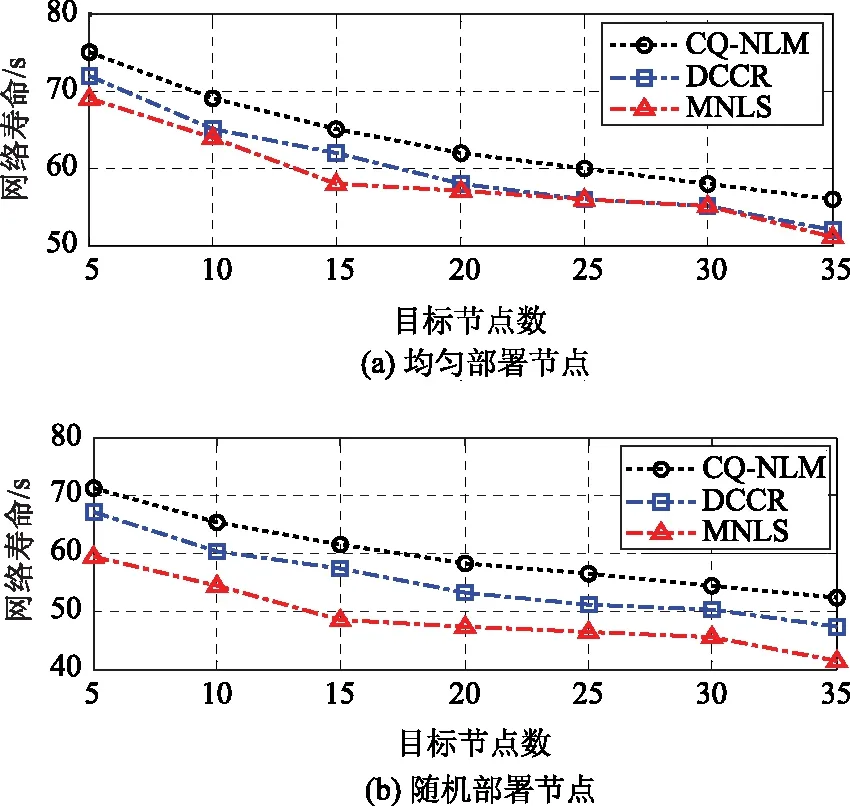
图6 网络寿命随节点部署方式的变化情况

图6(a)、6(b)分别描述了均匀部署、随机部署传感节点环境下三个算法的网络寿命。从图6可知，随机部署传感节点，降低了网络的总体寿命。原因在于：均匀部署传感节点，使节点分而更均匀，更有利于检测目标。而随机部署使得节点分布呈随机性，这不利于检测目标。因此，需要消耗更多的能量去检测目标，进而降低了网络寿命。

4 总 结

针对DSNs的目标覆盖问题，提出基于覆盖质量感知的最大化网络寿命CQ-NLM算法。CQ-NLM算法先利用概率感测模型，计算每个目标的覆盖质量。然后，建立目标函数，再利用MILP优化网络寿命，通过以最少的传感节点数，实现覆盖最大化。仿真数据表明，提出的CQ-NLM算法有效地提高网络寿命。