初中数学教学中“化归思想”的应用

■福建省莆田市秀屿区秀山初级中学 陈丽华

化归思想就是化复杂为简单，同样的数学问题对于有的学生来说很难，而有的学生却觉得很简单，这就是因为后者能够用现有的知识和已知条件，将问题抽丝剥茧，使答案呈现在眼前，这就是化归思想的运用。实际上，解答数学问题的本质就是运用化归思想的过程。基于化归思想的重要性，本文就重点探讨了在初中数学教学过程中应从哪些方面培养学生化归思想的应用能力。

一、化归思想的本质概述

初中数学是有一定难度的学科，涉及较多的公式、理论等，数学试题就是以考查学生这些理论、公式的掌握程度为目标，以某个或几个知识点为核心，设置相关已知条件，使学生利用这些已知条件、所涉及的理论及公式，求出问题的答案。数学问题看似存在一定难度，但实际上和现有知识息息相关，学生要想解决这些问题，就可通过化归思想，把看似复杂的问题通过已知条件来找到和其存在相互联系的知识点、公式，实现问题的化难为简、将原本生疏的问题转化为成自己所熟悉的知识点，将抽象化的问题转化为直观的视角，从而将答案梳理出来，这正是化归的思想的本质。

二、化归思想的内涵

化归思想不仅仅是数学解题思想，同时也是一种基本的逻辑思维策略，生活中许多的难题通过这种思想来转变思路，就可能实现化难为简，达到解决问题的目的，因此在初中数学中培养学生的化归思想，也符合新课标中提倡的培养综合素养的教学目的。

在数学中的化归思想，就是利用事物间的相互联系，在设置数学问题时，每个已知条件都是以围绕某个知识点、理论或公式出现的，学生要找到和这些已知条件相联系的知识点，把原本较难或陌生的问题条件，转化为和问题答案关系相近且已经学过的理论、公式，再将以运用，达到解决问题的目的。例如二元一次方程在求解过程中，就是利用相互间的联系，转化一元一次方程来求得答案；弓形面积就是通过扇形和三角形的差来实现化归，这都是化归思想在解决数学问题时的应用。

三、化归思想在初中数学教学中的应用

化归思想实际贯穿整个初中乃至更高阶段的数学学习中，掌握化归思想有助于帮助学生领悟数学的实用价值，学会通过现有数学知识发散思维、迁移思维。按照此种思想，还可用现有的数学知识来解决生活中相关联的实际问题。因此有效掌握基于化归思想的解题能力，不仅有助于提高学生的数学成绩，还能提升学生的数学学科素养，助其全面发展。

（一）列出化归思想解题过程，树立学生的化归意识

化归思想不像数学理论、公式那样可以直接传达给学生，让学生背下来。而是需要学生自己感悟，教师要在教学中引导学生认识并感悟化归思想，从而学会运用。要使学生有效掌握此种思想，首先可为学生列出一些通过化归思想的解题过程，使学生有一定的化归思想认识，在此基础上，再强化学生的数学基础知识，为学生梳理一些相互存在关联的知识点，并在教学中渗透化归思想的应用意识。

（二）化陌生为熟悉

在教学中发现，学生在做题时，对于自己熟悉的类型往往能够快速解答出来，但对于相对陌生的题型，往往思路闭塞，费尽脑筋也不一定能够做对。实际上，每个数学问题都是出题人根据当前所学知识出的问题，其本质都是一样的，所谓陌生题型，无非是换上件新衣服而已。如果学生能意识到这点，将新题型向以往做过的题型方向靠，实现陌生向熟悉的化归，转变为让自己更有思路的老题型，就能有效改善这一问题，比如这样一道二次根式题：

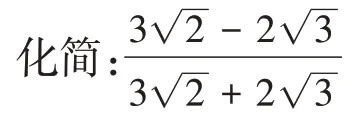
对于刚学习二次根式的学生来说，这种题型较为陌生，但我们在思考的时候可以采用化陌生为熟悉的方法，抓住问题的特点，将其转化为学生熟悉的旧知识点提取公因数以及分数问题，进行思考，就能得出以下解题方法。

解：

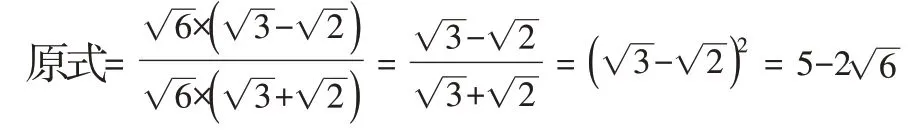
（三）化复杂为简单

在解题过程中，学生们经常能够见到题目很长的问题，这些题目学生会觉得特别复杂，但实际并不复杂。虽然题目冗长，但其中很多内容没有太多作用，学生在审题时先快速大致过一遍，最后再选择其中的题干部分，舍去可有可无的部分，精读其中题干，实现化复杂为简单，再将所得到的条件进行汇总，就能得到思路。以下面一道勾股定理相关的问题为例：

甲乙两渔船均在港口的同一个位置出海打渔，其中甲渔船是一艘大型的新船，乙渔船是一艘老旧的小渔船，甲渔船以正东南方向，每小时16 海里的速度行驶。乙渔船则是向正西南方向行驶，当两艘船均行驶1.5h 后，两船之间的直线距离是30 海里，那么请问乙渔船的时速是多少海里？

很多学生看到这一问题的文字较多，会有退缩的心理，实际上去掉一些无关条件，提取题干后，就剩几点而已。两船的出发点相同设为原点O，行驶1.5小时后，就形成了一个三角形,此时甲船所在位置设为A，乙船所在位置设为B。甲的速度和行驶时间是已知的，通过这两个条件可得OA距离，AB距离也是已知的，就是30 海里，求第三条边也就是OB。接着看其他条件，正东南方就是正南偏东45 度，正西南方就是正南偏西45度，那么这两艘船的行驶轨迹恰好是个直角。也就是说△AOB 为直角三角形，就可以根据已知的勾股定理公式a²+b²=c²，求出OA 的距离，再除以1.5 小时，就是乙船的时速。根据此题可以看出，很多看起来较为复杂的数学问题，在解题过程中，可画出反映各主体相互之间关系的条件，即关键条件，舍去不必要的条件，就能将复杂的问题向简单化归，有助于学生理清思路，得出答案。

（四）有效将定理公式化为已知条件

数学问题都是围绕着书中的定理、公式所出的，旨在考查学生是否能够真正理解并学会如何运用这些定理。因此在解答数学问题时，学生在读完问题后，脑海中找出相关的公式、定理，并将其作为已知条件，配合问题中的已知条件就能恍然大悟，得出问题的答案。比如在解答求三角形角度的问题中，已知条件一般不会给出三角形外角等于不相邻两内角之和，但做此类题的时候，学生应当将这一定理作为已知条件罗列出来。这就是要告诉学生，在做数学题时，千万不能只局限在题中给出的已知条件，还要想想所学的相关定理、公式，并和题中已知条件相结合，说不定就会柳暗花明，得出结果。

（五）化抽象为具体

数学本身就是一个较为抽象的学科，但学生的逻辑思维能力较差，很难将其有效理解，就可能导致没有思路。对于这样的情况，建议学生借助一些辅助的方式，化抽象为具体。为达到这一目的，学生将相关已知条件都罗列在草稿纸上，或通过列表格、画图表等方式，将抽象的问题具体地呈现在眼前，从而更能有效地理解与分析问题。

1.巩固学生的基础知识。能够有效运用化归思想，需要以扎实的基础知识水平为前提，比如概念、公式、理论等。通过前文也可看出，化归思想的运用离不开这些基础知识，因此学生必须以掌握这些基础知识作为前提，才能有效运用这些基础知识开展化归。教师在教学时就需要加强学生对于这些基础知识的理解与记忆，并为学生列举一些利用这些基础知识的化归情况，为其之后能够自主运用化归思想打下坚实的基础。

2.创新教学思维渗透化归思想。教师在教学时应当改变以往的应试教学思维，在解题教学时将数学基础知识和采用的数学思想合二为一，解出运用化归思想时的解题思路，让学生明白是以什么为导向，抓住了哪些联系，实现了化陌生为熟悉、化复杂为简单，强调思想运用过程的讲授，使学生能够有效理解化归思想，并掌握如何加以运用，经过几次示范及联系后，在教学时可要求学生自己说出化归的思路，并加以点评，帮助学生锻炼化归思想的实践能力。

四、结语

化归思想和其他数学解题思想不同，它不是直接去探求问题的答案，而是对问题进行转化。对于初中生来说，他们的逻辑思维能力、空间思维能力相对较差，解答问题时很容易被问题中多余的条件或陌生的题型所迷惑，看不清本质。而化归思想正是帮助学生将看似复杂的问题，抓住本质，转化为成更加直观、清晰、更易求得答案的形式，从而事半功倍，得出问题的答案。