突破弹性碰撞教与学的疑难点

万大林

(六盘水市广播电视大学 贵州 六盘水 553000)

1 问题的背景

动量及动量守恒是高中物理教材[1]的主要内容，也是大学基础物理教材[2]完整力学体系中不可或缺的重要组成部分．弹性碰撞是物理学研究中建立的一个极其重要的理想化模型，是大、中学物理教材中动量守恒定律与机械能守恒定律综合应用的典型范例，也是过去每年高考中的重要考查知识点．

自2006年本次高中课程改革以来，动量与动量守恒编入高中物理教材选修3-5模块，属于高考选考模块(特别说明：教育部考试中心根据改革以来的实际情况，2016年10月9日，公布了2017年普通高考考试大纲修订内容，重新将高中物理选修3-5模块纳入高考必考模块)．这样就使得动量及动量守恒的内容在大、中学教学过程中被弱化，从而也导致弹性碰撞问题的实际处理成为教与学的疑难点，突出体现在对一类二元二次方程组的解存在较大障碍．

2 对称完美的方程组

若干年来的教学实践中，在教授弹性碰撞之前，我们总坚持先上一节数学预备课，以先突破如以下形式的关于x和y的二元二次方程组的解，即

(1)

其中，a,b,p,q为常量.

因为，这样有助于很好地突破弹性碰撞教与学的疑难点．

这类方程组有着完美的对称性，其解法也存在很大的技巧．根据方程组的对称关系，原方程组可以变形为

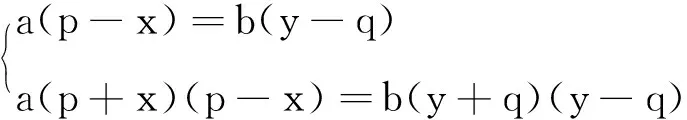
(2)

当p-x≠0，y-q≠0时，将式(2)中的第二方程式与第一方程式左右两边分别相除，可得

p+x=y+q

(3)

将式(3)代入式(2)中的第一方程式，易得

(4)

当p-x=0时，必有y-q=0．这种情况下原方程组的解为

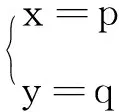
(5)

3 典型实例分析

有了一定的数学知识储备之后，在教授弹性碰撞的过程中根据学生的实际情况，通常给出一至二个典型实例分析．现举一例予以说明．

【题目】如图1所示，质量为m的弹性小球置于质量为M的弹性大球之上，两球恰好相互接触而无挤压，且两球球心连线始终呈竖直状态．让它们由静止开始下落h后大球将与水平地面发生碰撞，然后两球都将因反弹而上升．如果重力加速度为g，运动过程中空气阻力忽略不计．那么，两球质量在满足怎样的约束条件下，两球都能反弹达到各自的最大高度？它们反弹上升的最大高度各是多少？

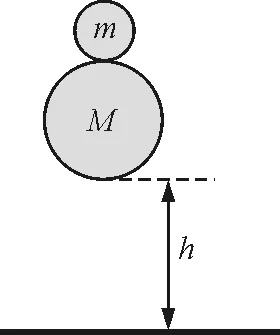
图1 题图弹性碰撞

解析：根据两球碰撞后都能向上运动，说明两球的质量关系满足m

(6)

显然，这一方程组与式(1)类似．因此，用前述相似的求解方法，即易得出与式(4)相似的解

(7)

(8)

分析式(8)不难得出，两球的质量相差越大，两球相互碰撞后的速度就都越大．当两球的质量关系满足m≪M时，两球相互碰撞后的速度都达到最大极限．即

(9)

因此，在这种情况下，两球均能反弹上升到各自最大高度的极限值．分别为

(10)

显然，这一模型中两球反弹各自上升的最大高度都是有限值．特别值得一提的是，这一模型的原型源于2002年全国高考广东卷第19题，由此也可略见弹性碰撞在人才选拔中的作用和地位．

4 结束语

中学教学是大学教学的基础，中学教学必须让学生牢固掌握最基本的基础知识，才能为大学教学做好铺垫．否则，学生即使升入大学也很难真正接受大学教学提升知识结构与能力．这方面，物理学科显得更为突出．

物理学科的学习与研究，都必须要有一定的数学知识储备．特别对于一线教师，这种数学知识储备必须相对足够．

弹性碰撞模型在宏观现象的研究中有着重要的作用，而且在微观粒子世界的研究中作用更为卓著．因此，在大、中学物理教学中都必须应该引起足够的重视．