长直交变电流磁场中圆线圈的感应电动势和感应电流

邹俊峻

(长安大学汽车学院 陕西 西安 710064)

在大学物理教材中,利用法拉第电磁感应定律求解变化磁场中导体线圈上的感应电动势的例子很多,如长直交变电流磁场中矩形线圈上的感应电动势，变化的均匀磁场中矩形线圈和圆形线圈上的感应电动势[1～3]．但是,对于长直交变电流磁场中圆形线圈上的电磁感应问题，很少有人求解过．在本文中,利用磁场的安培环路定理、法拉第电磁感应定律和高等数学知识,对这个问题进行了讨论,计算了导线与线圈圆心之间的距离大于线圈半径时线圈中的感应电动势和感应电流．

1 圆线圈中的感应电动势

如图1所示,已知无限长直导线AB中通有交变电流i(t)=I0sinωt，半径为R的平面圆形线圈与长直导线AB共面,导线与线圈圆心之间的距离为d，且有d>R.线圈处在导线AB的右边,线圈平面内磁场非均均分布,但方向总是相同．建立如图所示坐标系,在(r,θ)处取面积元dS=rdrdθ，由安培环路定理可得：长直交变电流i(t)在dS处所产生的磁感应强度大小为

(1)

方向垂直纸面向里．穿过dS的磁通为

(2)

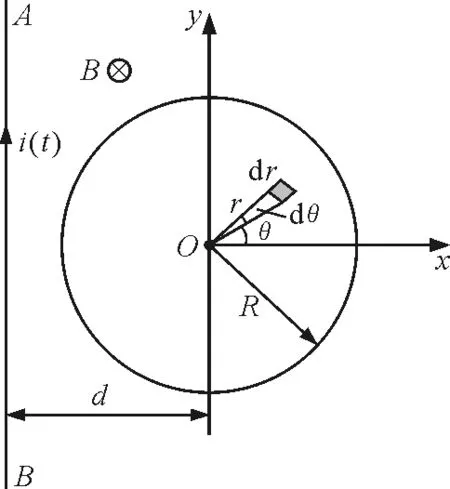
图1 圆形线圈平面的磁通(d>R)

则穿过圆形线圈的总磁通为

(3)

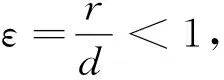
利用残数定理[4]可以求解函数I的积分,令z=eiθ,得

(4)

令

且f(z)的分母有两个一阶零点

和

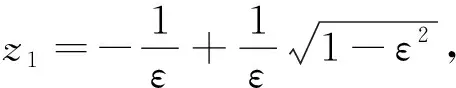
(5)

因此式(4)的积分为

(6)

将式(6)代入式(3),得穿过圆形线圈平面的总磁通为

(7)

由式(7)可知:载流直线和圆线圈之间的互感系数M为

(8)

由此可见，互感系数M只与它们之间的相对位置、圆线圈的尺寸以及介质有关，与长直交变电流大小无关．

由法拉第电磁感应定律可得圆形线圈中的感应电动势为

-Emcosωt

(9)

2 圆线圈中的感应电流

假设圆线圈的自感系数为L,等效电阻为r，感应电流为I(t),则圆线圈的等效电路如图2所示.

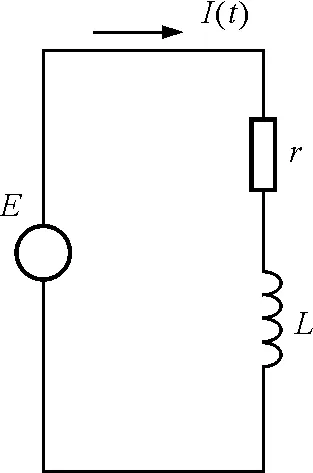
图2 圆形线圈平面的等效电路

由欧姆定律可得

(10)

即

(11)

式(11)是一阶线性非齐次微分方程[5],为了求其解,先求解一阶线性齐次微分方程

(12)

得

(13)

再令

(14)

代入式(11),化简可得

(15)

利用积分公式[6]

(16)

可得式(15)的解为

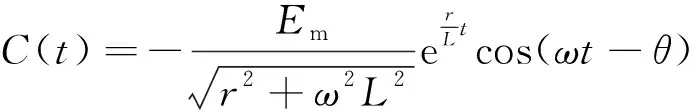
(17)

(18)

3 结论

综上所述, 本文计算了长直交变电流在共面圆形线圈中产生的感应电动势和感应电流．利用磁场的安培环路定理、法拉第电磁感应定律等物理原理，以及残数定理、一阶线性非齐次微分方程等高等数学知识,详细推导了导线与线圈圆心之间的距离大于线圈半径时圆形线圈中产生的感应电动势和感应电流，并得到了他们的解析表达式．希望本文可以为教师和同学们提供一些有用的参考,有利于同学们更好地掌握感应电动势和感应电流的求解方法以及高等数学知识的运算．