涂黄油吐司面包落地问题的力学分析*
2019-03-05米广宇
米广宇
(中国农业大学烟台研究院 山东 烟台 264043)
卓启同 吕洪凤
(中国农业大学理学院 北京 100083)
著名的墨菲定律[1]指出:如果有两种或两种以上的选择,而其中一种将导致灾难,则必定有人会作出这种选择.(If there are two or more ways to do something, and one of those ways can result in a catastrophe, then someone will do it.)
在生活中常常能看到这种观点:如果一片涂黄油的吐司面包从桌上掉落,一定是涂黄油面着地——因为这是最坏的结果.那么这个十分契合墨菲定律的现象为何会时常发生呢?这到底是偶然概率问题,还是必然的物理现象呢?
对于这个问题,前人已经有过一些研究,例如文献[1]用牛顿方程法和拉格朗日方程法对涂黄油吐司面包落地的过程建立了物理模型,并对涂黄油面包翻转角在不同条件下的角度做出了讨论,文献[2]则是从力学原理的角度,运用“降落伞效应”对此问题做出了定性分析[2].
现从一全新视角,将形状和大小相对稳定的吐司面包看作刚体,并运用动力学的相关知识对此进行分析.
1 涂黄油吐司面包落地前的情景模拟
如图1所示,给出涂黄油吐司面包从桌边滑落前的示意图,涂黄油的一面在上.为简化分析,假设黄油在吐司面包上涂抹均匀.涂抹上的薄层黄油的质量(约3 g)远小于吐司面包片的质量(约35 g),它对黄油吐司面包片整体的质心位置、惯性大小及其后的转动过程影响可以忽略[7].

图1 涂黄油吐司面包从桌边滑落示意图
假设吐司面包与黄油涂层的总质量为m,长度为L,面包与桌面的夹角为θ,面包的质心离开桌边的一小段距离为r,面包的质心速度v可分解为平行于面包平面的速度vτ(以速率标示)与垂直于面包平面的速度vn(以速率标示),面包绕质心轴的转动角速度为ω,转动惯量为Ic. 下面分析涂黄油吐司面包片从桌面掉落的条件.
分析面包掉落前的受力,绕面包与桌面接触点转动的力矩来自于重力mg,摩擦力f和支持力Fn对绕过接触点的转动无贡献,由转动定律可得
(1)
对于式(1)进行计算,乘以2ω并代入初始条件ω=0,θ=0,有
得到
(2)
质心加速度由系统合外力决定. 以质心为坐标原点,平行于面包平面的方向为x轴,垂直于面包平面向下的方向为y轴. 假设面包片倾斜到φ角度时开始沿斜面下滑,由受力分析知
(3)
(4)
f=μFn
(5)
由式(3)~(5)可知,沿着速度vτ方向的合力大于最大静摩擦力时,面包片跌落.相应的最大静摩擦因数
(6)
面包片下滑对应夹角为
(7)
涂黄油吐司面包离开桌面时的夹角与面包和桌面间的摩擦系数有关[5~7],与面包长度L和面包质心距离桌边距离r有关.
2 涂黄油吐司面包翻转过程分析
若取极限情况,不考虑面包从桌面滑落时摩擦力所做的功则在脱离桌面时,其势能之差将完全转变成质心的动能和绕质心轴的转动动能
(8)
从而得到
(9)
假设面包从开始倾斜到完全滑离桌面的时间为T,且在滑动中面包与桌面的夹角θ不变,则根据冲量定理,沿着x方向有
mgsinθT=mvτ
(10)

(11)
根据角动量定理(冲量矩定理):力矩在时间上的累积等于角动量的改变量,结合式(10),在T时刻有
(12)
离开桌面前,根据平行轴定理,面包绕接触点的转动惯量为
此刻的角动量为

(13)
比较式(12)和式(13)可得
(14)
将式(14)代入式(9) 得到
(15)
在脱离桌面后的自由下落过程中,面包的角动量守恒,其绕质心轴旋转的角速度不变,恰为T时刻脱离桌面时的角速度.假设桌面高h,下落时间在不考虑空气阻力时为
可近似取下落时间
则面包落到地面时的空中翻转角为
总翻转角度Ψ为
(16)


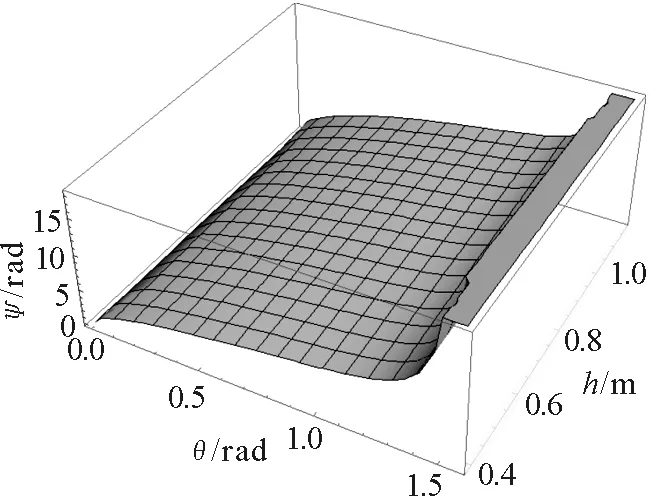
图2 总翻转角度Ψ三维变化图

3 公式在实际生活中的应用
将L=100 mm和h=780 mm代入式(16),可得到不同初始下滑角θ对应的总翻转角度Ψ.

表1 总翻转角度Ψ

图3 总翻转角度ψ图(弧度)

