渤海湾盆地沾化凹陷陆相页岩储层岩石力学特征及可压裂性研究
2019-03-05夏遵义马海洋
夏遵义,马海洋,房 堃
(1.北京大学 工学院,北京 100871;2.中国石油大学(华东) 石油工程学院,山东 青岛 266580)
我国页岩油气资源分布广泛,资源潜力巨大,是重要的非常规能源[1-4]。由于页岩储层自生自储、低孔低渗的特征,极大增加了其开采难度,必须经过体积压裂改造才能达到工业开采的目的[5-7]。页岩可压裂性指的是页岩储层经过水力压裂后可以被有效改造的性质,在页岩油气开发中是一项重要的评价参数[8-9]。对于页岩可压裂性的研究,目前尚未有统一的评价标准,JARVIE等[10]以页岩中石英的含量计算页岩脆性,认为石英含量高的页岩可压裂性好;RICKMAN等[11]认为杨氏模量和泊松比可反映页岩的脆性;刁海燕[12]结合力学参数和矿物成分对页岩的可压裂性进行评价;范宜仁等[13]考虑页岩天然裂缝及力学特性,对页岩的压裂潜力进行综合表征。由于页岩可压裂性反映的是页岩储层的综合特征,不能仅考虑矿物组成或力学参数,而天然裂缝等因素由于量化难度和成本较大,且易产生误差,无法有效应用。
本文以渤海湾盆地沾化凹陷始新统沙三下段陆相页岩为研究对象,通过室内实验测试其矿物成分及岩石力学参数,并结合实际地质及生产情况,测试成岩作用及围压等因素对页岩脆性的影响。综合考虑页岩矿物成分、力学参数、成岩作用及围压4个方面,建立可压裂系数数学模型,为页岩储层可压裂性的定量评价提供新方法。
1 实验样品
对沾化凹陷沙河街组沙三下段不同深度的27组页岩进行矿物成分测试,选取8块页岩进行岩石力学实验,其中Z1h、Z2h、Z3h、Z4h和Z5h样品均为平行层理面取样;Z2-1v、Z2-2v和Z2-3v为垂直层理面取样,与Z2h取自同一深度,为加热处理样品。8块样品基本信息如表1所示,有机碳含量(TOC)在1.54%~5.09%之间;镜质体反射率(Ro)介于0.56%~0.90%之间,平均为0.72%,有机质热演化程度处于低成熟—成熟阶段;有机质类型主要是Ⅰ型和Ⅱ1型;孔隙度介于4.08%~7.04%之间,平均为5.40%,渗透率在(4.66~15.05)×10-3μm2之间,平均为6.99×10-3μm2,属于低孔低渗储层。
2 实验方法
2.1 X射线衍射实验
实验利用美国伊诺斯公司研发的XRD Terra矿物成分测试仪完成。首先将样品磨碎至粉末状,利用筛网过筛,取适量粉末倒入样品槽中进行实验。实验完成后将得到的图谱峰值与数据库卡片进行对比,找到各峰值对应的矿物成分,最后计算矿物成分比例。
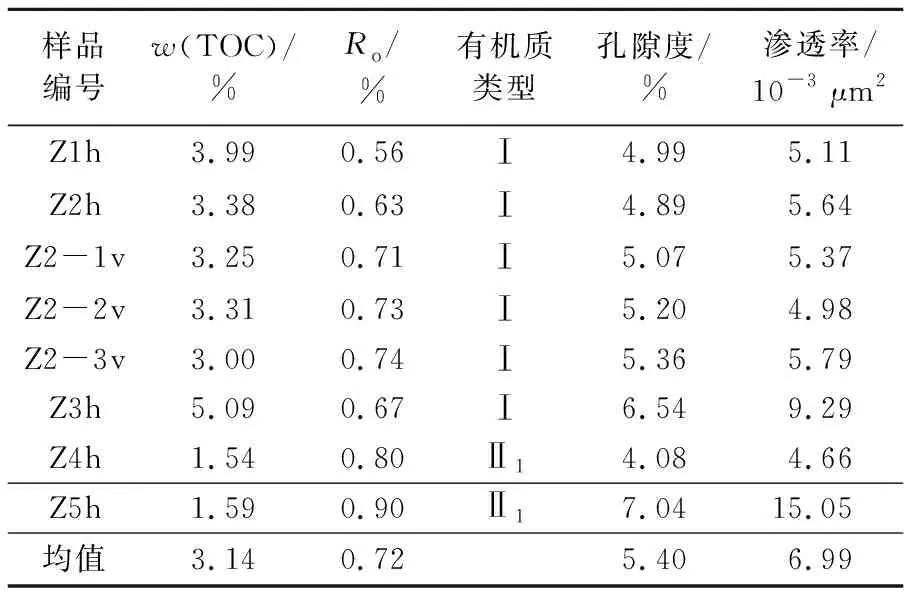
表1 渤海湾盆地沾化凹陷沙三下段页岩样品基础信息
2.2 岩石力学实验
实验采用美国MTS公司生产的MTS816型岩石力学测试系统完成。系统最大垂向压力1 000 kN,垂向活塞行程100 mm,最大围压140 MPa,围压室最高加热温度200 ℃。将页岩样品切割成Φ25 mm×H50 mm的标准圆柱岩样,上下端面磨平且与中轴线垂直,对其进行单轴及不同围压条件下的加载破坏,得到应力—应变曲线,进而计算得到抗压强度、杨氏模量和泊松比等岩石力学参数。
3 实验结果与分析
3.1 全岩矿物衍射
3.1.1 页岩矿物组成
对沾化凹陷沙三下段27块页岩样品进行了全岩矿物组分分析,不同页岩的矿物组成有一定的差异(图1)。沙三下段泥页岩矿物成分可分为3大类,分别为脆性矿物、碳酸盐矿物和黏土矿物。脆性矿物主要包括石英、长石和黄铁矿,其中石英和长石含量较多,分别为13%和12.1%;黄铁矿平均含量为5.1%,脆性矿物的存在有利于页岩的压裂改造。碳酸盐矿物主要包括方解石和白云石,方解石含量最高,平均为40.2%;白云石含量较少,平均为5.4%。黏土矿物主要包括伊利石、伊蒙混层、坡缕石、绿泥石和高岭石等,除高岭石含量较少外,其余成分含量差异较小;伊利石平均含量为8.1%,伊蒙混层含量平均为5.9%,绿泥石含量平均为5.8%,坡缕石含量平均为4.4%。黏土矿物主要表现为塑性,含量较多将不利于储层压裂改造。研究区碳酸盐矿物含量最高,平均为45.6%,脆性矿物总量占比30.1%,高于黏土矿物的24.3%,表明沙三下段页岩具有较高的储层改造潜力。
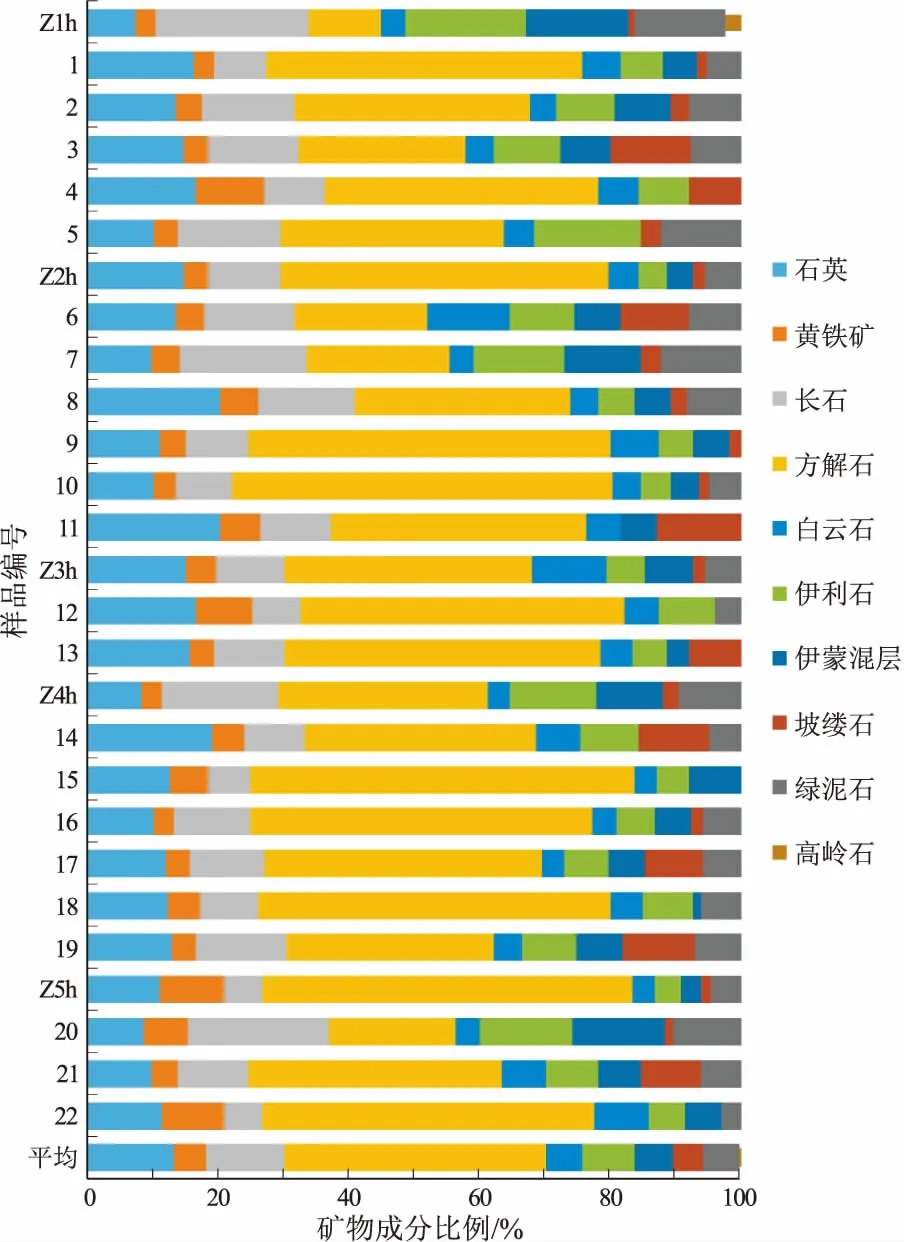
图1 渤海湾盆地沾化凹陷沙三下段页岩矿物组成
将各样品的脆性矿物、碳酸盐矿物、黏土矿物组成制成三元图(图2),根据矿物含量将其划分为硅质页岩、钙质页岩、黏土质页岩和混合页岩4类岩性。所测沙三下段页岩样品以混合页岩和钙质页岩为主,且混合页岩大部分偏向钙质页岩区域,黏土质页岩仅有一个,没有硅质页岩,表明碳酸盐矿物对页岩性质的影响不可忽略。
3.1.2 基于页岩矿物组成的脆性指数
一般来说,石英、长石和黄铁矿等是页岩中最重要的脆性矿物,它们的含量在很大程度上决定了页岩储层的脆性和可压裂性[14-18]。但随着岩石物理学和矿物学的深入研究,发现碳酸盐矿物也可以增加页岩的脆性[14-15],而研究区页岩中碳酸盐矿物含量高,因此,基于沙三下段页岩矿物组成的脆性指数计算公式为:
(1)
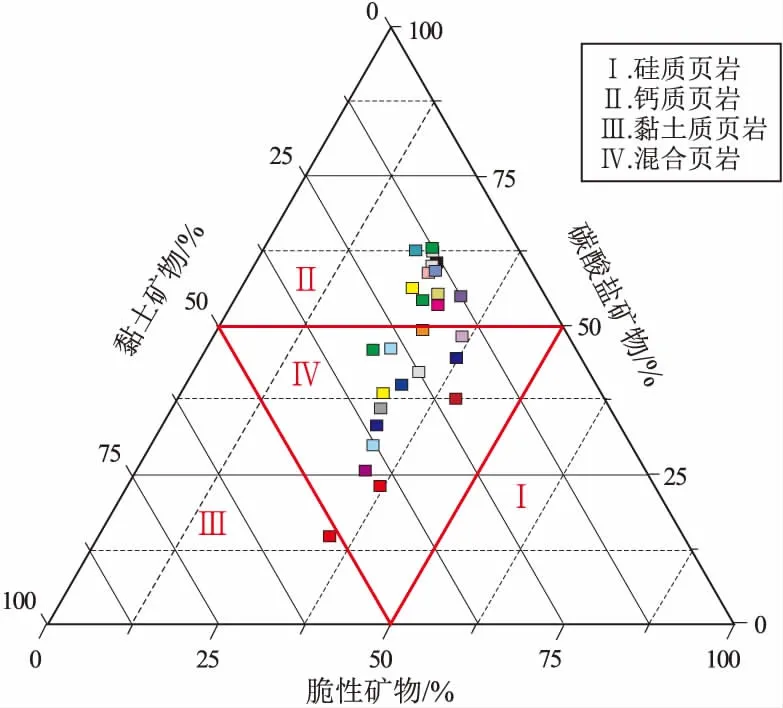
图2 渤海湾盆地沾化凹陷沙三下段页岩矿物组分三元图
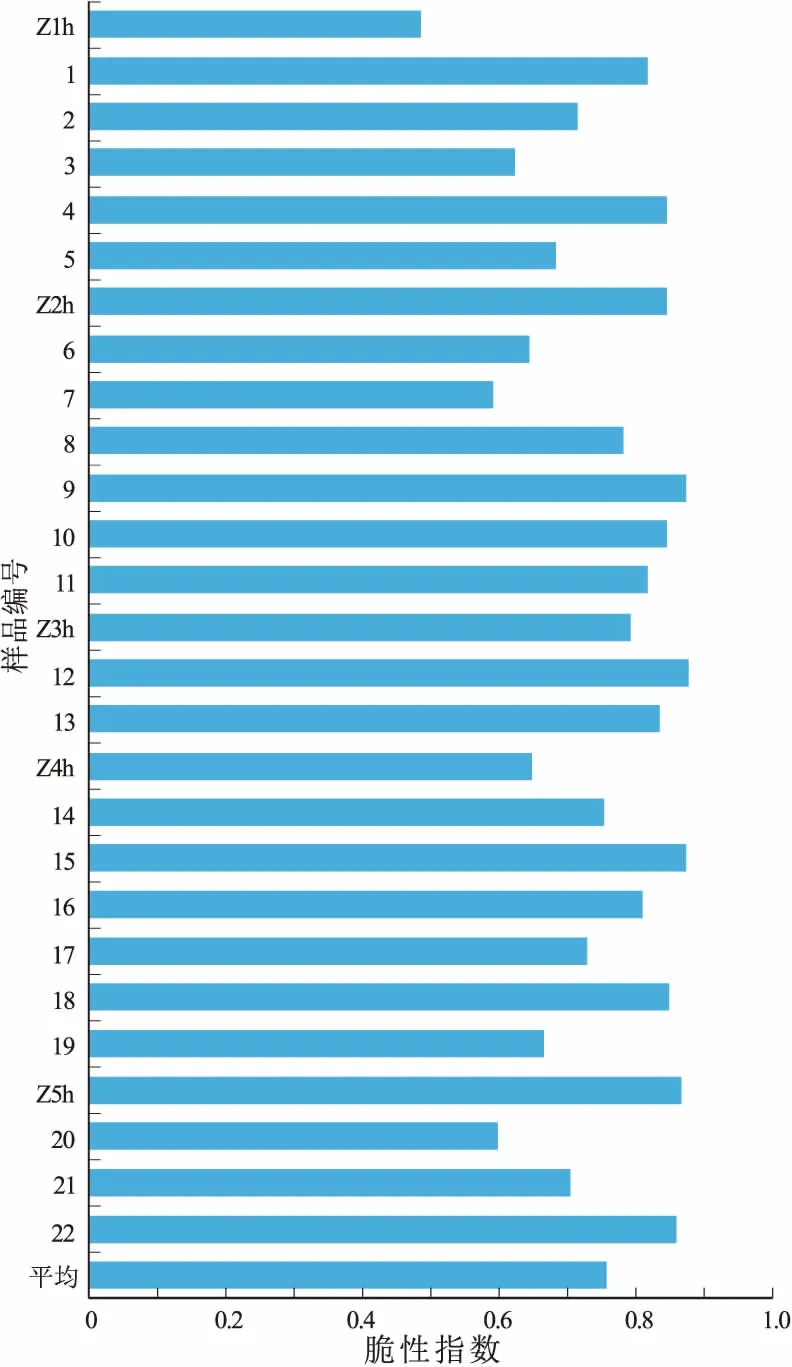
图3 渤海湾盆地沾化凹陷沙三下段页岩基于矿物组分的脆性指数
式中:B1为基于页岩矿物组成的脆性指数;Cb为脆性矿物含量;Cc为碳酸盐矿物含量;Ct为总矿物含量;所有变量均为无量纲。
由计算结果图3可知,沙三下段页岩基于矿物组分的脆性指数普遍较高,上下部分分布无明显规律,介于0.49~0.88之间,平均为0.76。这说明在矿物组分特征上,研究区页岩具有较好的可压裂性。
3.2 页岩岩石力学实验
3.2.1 单轴力学实验
图4a为页岩单轴压缩的应力应变曲线,可以看出,页岩样品在单轴压缩下的脆性特征较为明显,初始阶段压密上凹现象不明显,很快进入直线段,即线弹性变形阶段,此阶段页岩力学性质稳定,卸载后基本不受影响;未见明显的塑性特征,屈服阶段不明显,直至达到最大抗压强度试样破坏,峰后应力迅速下降。
研究区样品单轴压缩实验获得的岩石力学参数见表2,样品抗压强度范围是43.61~125.08 MPa,平均为74.55 MPa,与砂岩或碳酸盐岩相比较小(100 MPa左右);杨氏模量介于34.25~53.05 GPa之间,平均为41.64 GPa;泊松比在0.20~0.33,平均为0.26。根据SONDERGELD等[19]的研究发现,当杨氏模量大于24 GPa,泊松比小于0.25时,有利于页岩储层形成缝网结构。研究区页岩的杨氏模量远大于该指标,且泊松比也较为接近,表明该段可采用体积压裂进行改造。
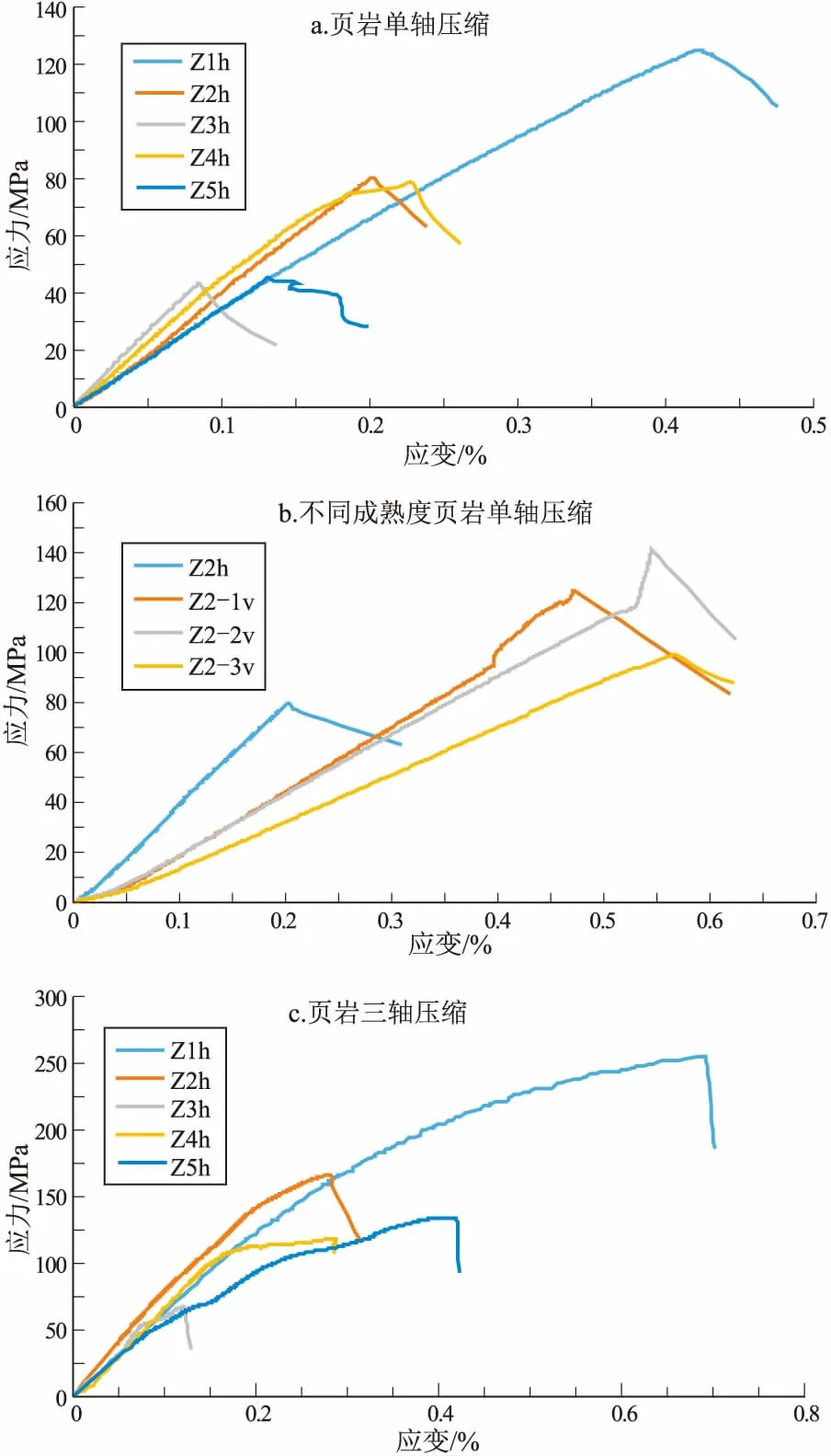
图4 渤海湾盆地沾化凹陷沙三下段页岩应力应变曲线
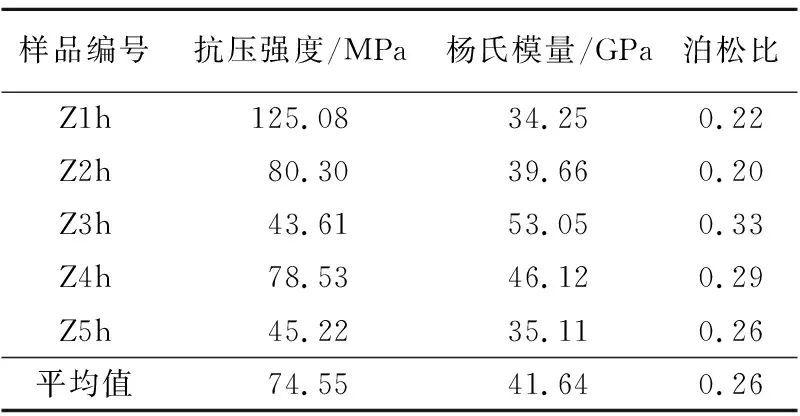
样品编号抗压强度/MPa杨氏模量/GPa泊松比Z1h125.0834.250.22Z2h80.3039.660.20Z3h43.6153.050.33Z4h78.5346.120.29Z5h45.2235.110.26平均值74.5541.640.26
3.2.2 不同成熟度页岩单轴力学实验
为了研究成岩作用对页岩岩石力学性质的影响,将同一深度取心的岩样Z2-1v、Z2-2v和Z2-3v经过加热处理,温度分别为321.6,336,360.4 ℃,对应成熟度Ro为0.71%,0.73%,0.74%,获得单轴压缩应力应变曲线(图4b),其中Z2h为平行于层理面取样,Z2-1v、Z2-2v和Z2-3v为垂直于层理面取样。与Z2h不同,其余3个柱样初始压密阶段较为明显,可能是由于层理缝受压闭合导致的;线弹性阶段较长,轴向应变普遍偏大,且屈服应力点较为明显。
表3为不同成熟度页岩单轴压缩的岩石力学参数,3组样品的抗压强度介于99.04~142.02 MPa,平均为121.99 MPa。研究发现垂直样的抗压强度一般为水平样的2倍左右[20],Z2h样品的抗压强度为80.30 MPa,明显高于另外三组垂直样抗压强度的1/2。实验结果表明,高成熟度会使抗压强度下降。另外,杨氏模量和泊松比也都随着Ro的增大而减小。
3.2.3 页岩三轴力学实验
为了获得岩样在真实地层条件下的岩石力学参数,根据取样深度,确定加载围压为40 MPa。图4c为40 MPa围压下岩样三轴压缩应力应变曲线,由于围压的影响,无初始压密阶段,曲线后部逐渐变弯呈现塑性特征,屈服段较长,屈服应力点较为明显,不同岩样破坏时应变差异较大。
沙三下段页岩在不同围压下的岩石力学参数(表4)与单轴力学实验(表2)相比,三轴力学实验的抗压强度平均值从74.55 MPa增大到148.66 MPa,增大了近1倍;另外,从单轴到围压40 MPa,杨氏模量及泊松比均不同程度增大。可见围压对页岩的岩石力学性质影响较大。
图5显示页岩样品在单轴和三轴(40MPa)压缩下的破裂形态完全不同。分析认为,由于页岩层理明显且微裂缝发育,单轴压缩时容易从薄弱的层理面或微裂缝产生破坏,抗压强度小,容易从多处起裂,以劈裂式破坏为主;加围压后,由于围压的作用,岩样的层理或微裂缝被压紧,对岩样的破坏影响变小,抗压强度增大,岩样多以剪切破坏为主。
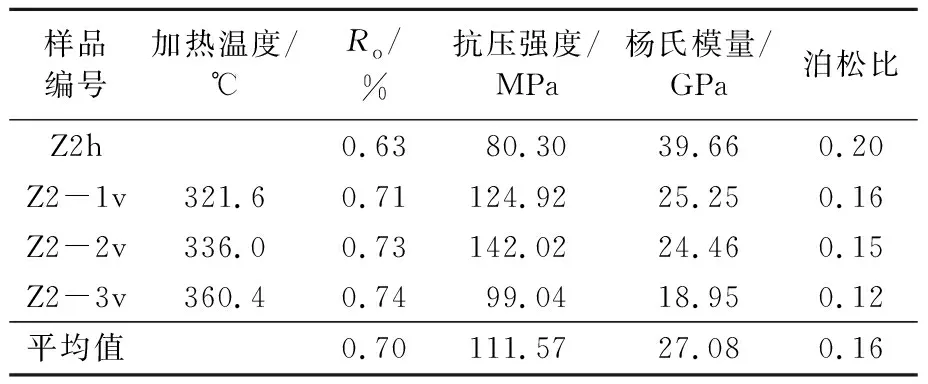
表3 渤海湾盆地沾化凹陷沙三下段不同成熟度页岩单轴压缩的岩石力学参数

图5 渤海湾盆地沾化凹陷沙三下段页岩破裂形态

样品编号抗压强度/MPa杨氏模量/GPa泊松比Z1h254.5647.890.34Z2h166.8577.740.41Z3h68.0560.780.42Z4h118.9869.940.43Z5h134.8458.010.43平均值148.6662.870.41
3.2.4 基于岩石力学参数的脆性指数
基于岩石力学参数计算页岩脆性指数的方法有很多,一般涉及到杨氏模量、泊松比、抗压强度、抗张强度、抗剪强度和断裂韧性等参数[12,15,21-25]。常用的弹性参数法认为杨氏模量越高,泊松比越小,页岩的脆性越高[11],式(2)~(4)为其具体计算方法。
(2)
(3)
(4)
式中:EB2为归一化杨氏模量;Emin、Emax为研究区杨氏模量最小值和最大值;μB2为归一化泊松比;μmax和μmin为研究区泊松比最大值和最小值;B2为基于岩石力学参数的脆性指数;所有变量均为无量纲。
计算结果如图6所示。由图6a可以看出,随着Ro的增大,页岩的脆性指数也相应增大。分析认为[8,26],在Ro值较低时,由于黏土矿物成分之间的转化等作用,容易造成孔隙、裂缝的充填,不利于压裂;随着成熟度增加,岩石矿物会向更脆且稳定的组分转化增加页岩的脆性,另外有机质热裂解产气还会增加页岩孔隙度,页岩气在页岩内部产生压力造成微裂缝,这一系列的作用使页岩的可压裂性得到提高。由图6b可见,从单轴压缩到40 MPa围压的三轴压缩,沙三下段页岩的脆性指数均有不同程度下降。结合图5可知,由于围压条件抑制了微裂缝的扩张,不易产生多裂缝,使页岩的可压裂性降低。
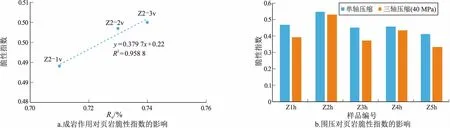
图6 渤海湾盆地沾化凹陷沙三下段页岩脆性指数影响因素
4 页岩可压裂性评价
页岩储层的可压裂性评价涉及诸多因素,主要包括页岩中脆性矿物含量、岩石力学性质、成岩作用和天然裂缝等,需要对各因素在可压裂性评价中所占的权重问题进行研究。由于天然裂缝难以量化,人为因素对结果影响较大,因此其参考意义具有局限性。压裂施工是在真实地层条件下进行的,根据实验结果得知,围压对页岩可压裂性的影响较大,考虑围压更符合实际生产情况。因此,需综合考虑页岩的矿物脆性指数、岩石力学脆性指数、成岩作用及围压等因素。首先利用极差变换法将各参数标准化,再采用层次分析法确定各因素对页岩可压裂性影响所占的权重,最后通过线性加权得到可压裂系数数学模型。
4.1 参数标准化处理
由于各因素的量纲不同,需采用极差变换法将其进行标准化处理[26]。根据实验结果将影响因素分为正向指标,即与可压裂性呈正相关的参数,包括矿物脆性指数、岩石力学脆性指数和成岩作用;负向指标主要是围压,即与可压裂性呈负相关的参数。计算方法如式(5)和(6)所示。
正向指标:
(5)
负向指标:
(6)
式中:S为参数标准化处理后的值;X为参数值;Xmin为参数最小值;Xmax为参数最大值。参数经过标准化处理后,数值均介于0~1之间,无量纲,数值越大越好。
4.2 层次分析法确定权重
各因素对可压裂性的影响程度需要进行量化,才能准确地评价页岩的可压裂性,利用层次分析法(AHP)可以确定各参数的权重。AHP是将研究的问题分成若干影响因素,并对各因素进行层次划分,对每一层的因素两两对比,确定各因素的相对重要性并给出相应的标度,建立矩阵求取权重[27-29]。具体步骤是将矿物脆性指数、岩石力学脆性指数、成岩作用及围压划分为同一层,两两比较,依据SAATY的1~9标度法[24]对各因素的相对重要性进行赋值,建立判断矩阵;根据实验结果确定判断矩阵取值(表5),然后通过和积法对判断矩阵的最大特征值和特征向量进行求解,最后利用最大特征值检验判断矩阵的一致性。
求得判断矩阵的特征向量为W=(0.29,0.52,0.12,0.07),即矿物脆性指数、岩石力学脆性指数、成岩作用和围压在可压裂性评价数学模型中的权重分别为0.29,0.52,0.12,0.07,且判断矩阵的一致性检验系数为0.013<0.1,符合一致性要求。
4.3 可压裂系数数学模型
依据层次分析法求得的各影响因子的权重,经过加权得到可压裂系数计算公式:
F=0.29B1+0.52B2+0.12D+0.07C
(7)
式中:F为页岩可压裂系数;B1为标准化矿物脆性
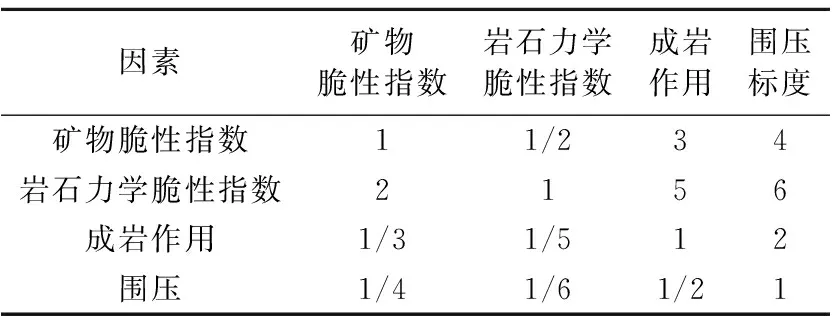
表5 渤海湾盆地沾化凹陷沙三下段页岩储层判断矩阵取值
指数;B2为标准化岩石力学脆性指数;D为成岩作用,以标准化Ro值为参数;C为标准化围压值,均为无量纲。
利用页岩可压裂系数数学模型对沾化凹陷沙三下段页岩的可压裂性进行评价。根据计算结果,Z1h、Z2h、Z3h、Z4h和Z5h的可压裂系数分别为0.290,0.853,0.445,0.396,0.410。沙三下段页岩可压裂系数介于0.290~0.853,平均为0.479。不同层位可压裂性差异较大,其中以Z2h样品所在层位可压裂系数最大,为0.853,单从可压裂性来看,可优选其作为压裂层段。
5 结论
(1)沾化凹陷沙三下段页岩矿物成分中碳酸盐矿物含量最高,平均为44.93%,脆性矿物含量次之,为30.98%,黏土矿物最少,平均为24.09%;以混合页岩和钙质页岩为主,该区矿物成分特点有利于页岩的压裂。
(2)单轴力学实验中沙三下段页岩抗压强度与砂岩或碳酸盐岩相比较小,平均为74.55 MPa,杨氏模量和泊松比平均值分别为41.64 GPa和0.26,以多裂缝的劈裂式破坏为主;加围压后抗压强度、杨氏模量和泊松比均有增大,为剪切式破裂,可压裂性降低;随着热成熟度增高,页岩的抗压强度、杨氏模量和泊松比均有降低,可压裂性增强。
(3)结合实验结果和实际地质情况,综合考虑页岩的矿物脆性指数、岩石力学脆性指数、成岩作用及围压等因素,利用层次分析法确定各因素对页岩可压裂性影响的权重分别为0.29,0.52,0.12,0.07;据此建立页岩可压裂系数数学模型,计算得到沙三下段页岩可压裂系数平均为0.479,不同层位存在一定差异,需经过优选才能进行压裂改造。
