高速铁路扣件弹条性能分析及频响特性研究

施何瑛，王安斌，高晓刚

(上海工程技术大学 城市轨道交通学院，上海 201620)

高速铁路无砟轨道扣件系统是轨道结构重要组成的一部分，弹条作为扣件系统的关键部分，起固定钢轨、保持轨距、吸收来自钢轨的冲击等作用，扣件系统的稳定性直接影响高速列车运行的安全性和舒适性[1]。弹条一旦发生失效，轮轨之间相互作用力会极具加剧，缩短扣件的使用寿命，严重时会引起列车脱轨。因此，开展弹条性能参数及频响研究，分析各动静参数之间的关联影响，对扣件系统设计的具有一定理论指导意义。

对于扣件系统，大量国内外学者从不同角度对其进行研究与分析。文献[1]采用FMECA分析法和故障树分析法对W300型扣件系统进行结构分析，找出扣件易损部分，并结合现场故障对整个扣件系统可靠性进行评估。文献[2]运用有限元软件分析WJ-7型弹条在不同冲击力作用下弹条最大应力发生的位置以及最大应力值，结果表明弹条在与铁垫板接触区产生最大应力，应力值为1 853 MPa。文献[3]从时频域角度研究分析e型弹条断裂的根本原因，结合现场测试结果，揭示弹条断裂的主要外因是弹条自然状态下和服役状态下的前两阶频率与现场波磨通过频率发生共振。文献[4]从动力学角度，研究扣件在高速列车动荷载作用下的振动特性，以Vossloh弹条为研究对象，基于非线性接触理论，得到弹条在安装状态下及列车动荷载作用下的振动特性，并于现场实测结果对比验证。揭示了弹条在螺栓预紧力为33 kN时达到正常安装状态，此时弹条中环位移为20.3 mm，扣压力为13.8 kN。文献[5]建立扣件系统有限元模型，研究扣件系统轨下胶垫的位移以及应力。文献[6]基于非线性动力学理论，分析扣件系统橡胶隔振器的振动特性。

综上可见，国内外学者对扣件系统的研究很多，但是很多研究只是基于独立的弹条或者扣件系统的其他部分而非针对弹条研究，并且缺少理论研究之后的实测验证。基于此，本文以某型高铁扣件SKL-15型弹条为例，采用ABAQUS有限元软件建立详细的扣件结构，基于模态理论和现场弹条频响分析，得到弹条在安装过程中的性能参数关系及振动频响特性。

1 扣件弹条建模

弹条由于线形复杂、参数多且相互关联，成为扣件系统设计的难点。为了能准确模拟扣件在安装状态下的性能，本文扣件系统各个零件均按照标准尺寸建模。其中弹条模型通过“中心线扫描法”建立模型，中心线主要通过Solidworks中的二次“投影曲线”和二次“组合曲线”操作完成，在建模时要注意弹条每个视图所对应的曲线，并且找准点与点、线与线之间的几何关系。弹条模型如下图1。

图1 某型扣件SKL15弹条模型

2 弹条模态理论和频响理论

2.1 模态分析理论

结构的振动特性决定自身以及与其关联系统的动态响应特性，模态分析[7]的主要作用就是确定结构和机械零部件的振动特性。根据弹性力学理论知识，建立扣件系统无阻尼运动方程为

把由机械系统的n个主阵型（即主模态）按阶次排序成一个n阶方阵（或振型矩阵）。

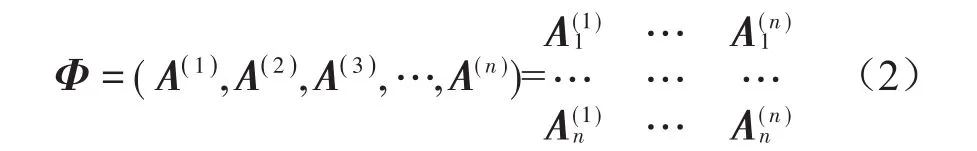
以模态矩阵对该方程作线性变换

变换后得到模态方程为

式中：M为模态质量矩阵，K为模态刚度矩阵。

对应的特征方程为

式中：ω2为弹条系统第i阶的模态固有频率，且i=1，2，3，…，n坐标变换矩阵Φ对应的每一列即模态振型。

2.2 频响理论

频率响应法是利用控制系统的正弦输入信号与相应输出信号之间的关系来分析系统性能的方法。频响函数是响应和力经过傅里叶变换之后的比值。且频响函数对结构的动力特性测试具有特殊重要的意义。假设在一个线性系统中，激励为X(t)，响应为Y(t)，对激励和响应这两个时域信号进行傅里叶变换得到它们的频谱X(ω)，Y(ω)，则可得到频响函数

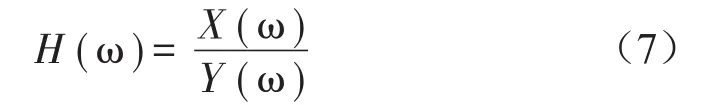
式中：X(ω)为激励频谱；Y(ω)为响应频谱。

3 某型扣件SKL15弹条仿真分析

3.1 有限元模型约束设置

为了使得模拟结果更接近真实情况，模型采用非线性接触[9-10]理论来处理扣件系统的边界条件。模型中将钢轨考虑为解析刚体，其他弹条接触区均根据真实几何尺寸装配，定义彼此间合适的接触关系。其中，法向接触采用ABAQUS软件中的“Hard”，即两物体间不允许相互贯穿或者侵入，接触面减的法向接触只能是压力[11]；切向接触采用库伦摩擦模型，并且引入一个允许“弹性滑动“的罚摩擦公式来处理粘结和滑移两种状态间的不连续性可能导致不收敛问题[12]。

3.2 材料参数

轨下刚度为26 kN/mm，接触面间的摩擦系数为0.3。

表1 材料参数

3.3 自由状态模态分析

为了解弹条自由状态下的固有振型，模型中未对弹条设置任何接触或者约束，考虑弹条在2 000 Hz以内的固有频率[13]，其前4阶振型图如图2(a)－图2(d)所示。

图中实线部分代表原始状态，阴影部分为变化振型，从振型图中可看出在频率为440 Hz时，弹条侧肢出现翻转振型，且最大应变出现在弹条跟部，这与现场弹条出现问题的位置一致，由此推测弹条在该频率下长期运动会导致弹条疲劳失效。详细振型描述如下表2。

图2 前4阶振型图

3.4 组装状态下模态分析

为研究弹条在服役状态下的频率以及振型特点，对弹条进行组装模态分析，考虑到高铁现场轮轨激励关注频段，组装模态同样考虑2 000 Hz以内的频率，有限元模型如图3所示，详细振型描述如表3所示。

图3 组装扣件有限元模型

表2 弹条自由状态下固有频率及振型

表3 弹条服役态下固有频率以及振型

3.5 不同扭矩下弹条性能参数分析

为了分析不同安装扭矩下组装弹条参数的性能。按照标准要求安装扣件系统，通过调节不同的螺栓扭矩，得到弹条在正常组装状态下的中环位移、螺栓预紧力以及扣压力，结果如表4及图4。按照供货条件，此型扣件扭矩一般为250 N∙m，当扣压力达到9 kN时，弹程为13.4 mm。

4 轨道结构频响分析

为进一步了解弹条频响特性，分析弹条在正常安装状态下的敏感频率，在某高铁试验段进行了轨道结构频响测试，如图5。

由图6可知，弹条弹跟和弹拱的峰值频率184 Hz为扣件支承刚度主导的弹条垂向固有频率；弹条峰值频率620 Hz与组装模态所得632 Hz基本吻合，可能为组装扣件系统弹条共振频率，最后导致扣件疲劳失效。

表4 组装状态下扣件性能参数表

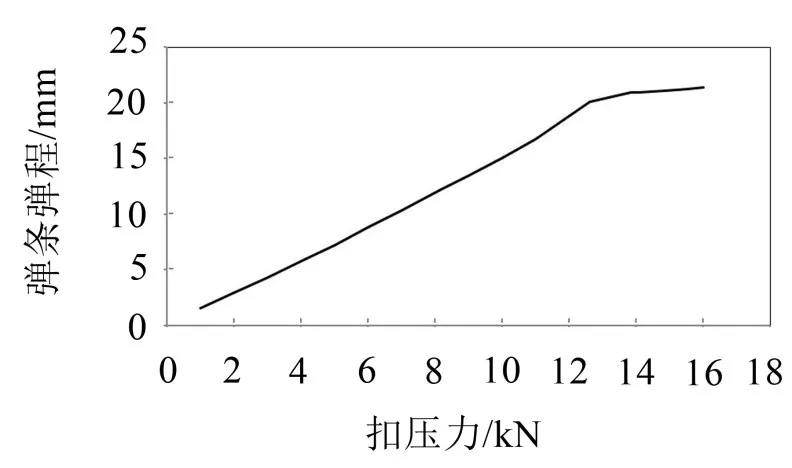
图4 扣压力结果图

图5 轨道结构频响测试图

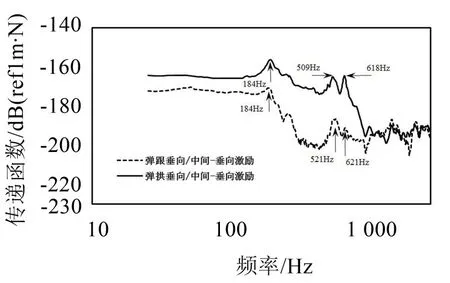
图6 频响分析图

5 结语

(1)综合考虑弹条在自由状态以及正常组装状态下的振动特性，得到弹条同振型的模态频率，分别是297 Hz、440 Hz、758 Hz、1 292 Hz和363 Hz、632 Hz、1 233 Hz、1 645 Hz。

(2)通过室内扭矩试验，得到弹条在正常组装条件下不同扭矩与扣压力和弹程的关系，按照此型扣件供货条件，当扭矩为250 N∙m时，扣压力为9 kN，此时弹程为13.4 mm。

(3)根据某高铁试验段的轨道结构频响测试，得到弹条频响分析结果，弹条峰值频率约620 Hz与模态频率632 Hz基本吻合，可能引起扣件系统共振，导致弹条疲劳失效。