助老机器人伴行模态振动对手部舒适性影响分析
2019-03-05穆小奇张小栋王亚宾韩焕杰
穆小奇,张小栋,2,王亚宾,韩焕杰
(1.西安交通大学 机械工程学院,西安 710049;2.西安交通大学 陕西省智能机器人重点实验室,西安 710049)
随着很多国家迅速步入老龄化社会,越来越多的老年人患有运动机能障碍。由于神经系统控制能力下降、肌肉力量降低等原因引起老年人下肢虚弱,而从事护理工作的年轻人员短缺又日益严重,因此特别需要开发助老机器人来代替护士和家人照看老年人。目前,很多学者研究了各种老年人助行机器人[1-9]。然而,在助行机器人帮助老年人行走的过程中往往会遇到地面不平或瞬时冲击现象,由此而产生的振动会引起老年人局部振动或者全身振动,有可能导致老年人不舒适。因此,对助行机器人的振动舒适性研究显得尤为重要。
近年来,对助行机器人的振动舒适性研究主要有:Noda Y等研究了基于振动频率的轮椅舒适性评估[10];Maeda S等研究了使轮椅振动幅值最小化来改善乘客舒适度[11];Hikmawan M F等采用半轮椅模型方法对电动轮椅乘客舒适性进行了分析[12];Matsuoka Y等建立了振动传输模型和振动舒适性评估模型,并把此两种模型组成舒适度评价预测系统,对轮椅-乘客系统进行了舒适性评价[13]。
目前,对助行机器人的舒适性的研究大多数是研究轮椅的振动舒适性,即仅考虑使用者的全身振动来分析机器人的振动舒适性。而对具有辅助老年人行走功能的机器人的振动舒适性只有较少的研究,即较少考虑老年人的局部振动。
本实验室自主开发设计了一台助老机器人[14-17],该机器人具有助力伴行、轮椅输送两大主要功能。本文研究在该机器人助力伴行工况下,当遇到地面不平或瞬时冲击现象时,老年人手部的局部振动。通过分析局部振动的幅值和振动最大速率来判定机器人的振动舒适性。
1 助老机器人及老年人手部的振动模型
为了研究助老机器人的振动舒适性,在此,通过对老年人手部的舒适性的分析来反映设计的助老机器人能否让老年人感到舒适。
以具有垂直和俯仰两自由度的助老机器人振动系统为研究对象。假设:因路面不平或瞬时冲击在助老机器人前、后轮所产生的位移输入分别为q1(t)和q2(t),在分析计算机器人和手部的整体振动时,忽略老年人手部的质量,把机器人整体振动简化为双轴两自由度振动模型,如图1所示。
图1(a)中,机器人重心G1为坐标原点;S1和S2分别表示前、后轮与地面的接触点;P1点表示机器人两把手连线的中点;两前、后轮与地面的接触刚度,即两前、后轮轮胎的刚度,分别用k1、k2表示;接触阻尼,即两前、后轮轮胎的阻尼,分别用c1、c2表示;参数k1、k2、c1和c2可通过对前后轮分别施加向下的激励,利用位移传感器测得垂直方向位移的响应并得到其频域数据,通过对频域数据进行最小二乘法参数识别获得;图1(b)中,S1′和S2′分别表示前、后轮与地面的接触点在前、后轮的位移输入q1(t)和q2(t)下,发生垂直与俯仰运动后的变化两点;G2点表示机器人静平衡位置重心G1发生垂直与俯仰运动后的变化点;q(t)表示重心偏离静平衡位置的位移,θ(t)表示绕重心的转角;l2和l1分别表示重心到前、后轮的水平距离;机器人质量为m,系统绕重心轴的转动惯量为J,列出机器人整体平面振动微分方程。

图1 机器人的双轴2自由度振动模型图
如式(1)和式(2)。

在助老机器人前、后轮分别受到位移输入q1(t)和q2(t)下,会引起老年人与机器人两把手接触位置坐标分别发生变化。为便于模型简化及计算,把老年人与机器人两把手接触位置处简化到两把手连线的中点P1位置处。假设P2为P1变化后的点,其坐标为(P2x,P2y)。根据机器人的几何关系(如图2所示)。

图2 机器人的几何关系图
列方程(3)和方程(4)
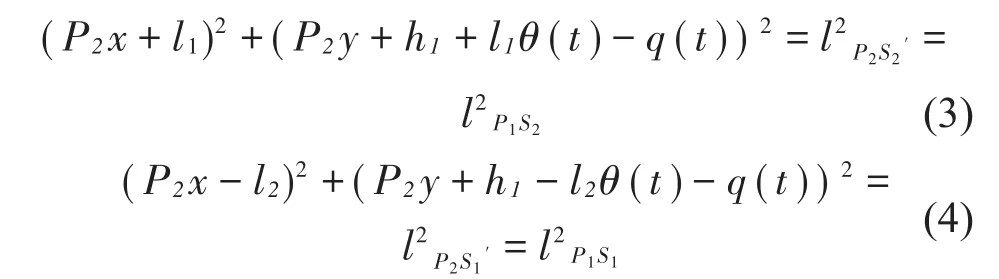
则,由P1点运动到P2点的水平位移rx(t)和竖直位移ry(t),如方程(5)和方程(6)所示
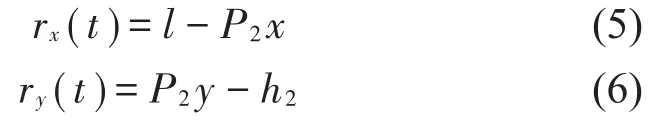
假设,机器人两把手连线的中点P1处水平方向的接触刚度和接触阻尼,即老年人手部水平分布刚度和阻尼,分别如k3、c3;垂直方向的接触刚度和接触阻尼,即老年人手部垂直分布刚度和阻尼,分别如k4、c4。参数k3、k4、c3和c4可通过对老年人手部施加激励,利用加速度计测得相应加速度的响应,经滤波处理并推算出相应水平方向和垂直方向的位移响应并得到其频域数据,通过对频域数据进行最小二乘法参数识别获得;老年人手部的振动模型如图3所示。
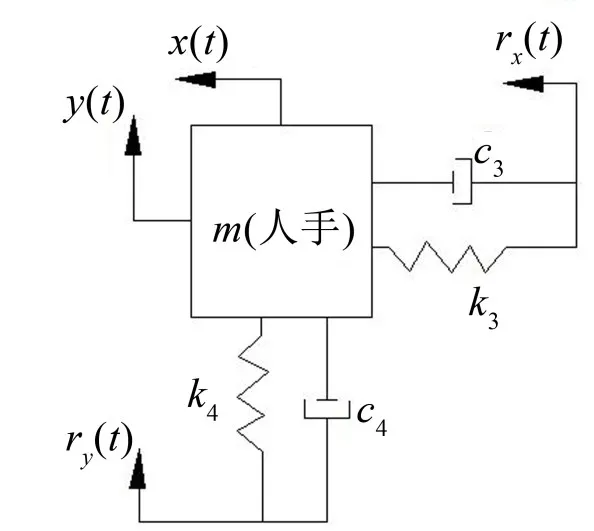
图3 老年人手部的振动模型图
分别列出水平方向和竖直方向的老年人手部的振动微分方程。如式(7)和式(8)

2 对老年人伴行舒适性影响分析
舒适性本身是一种主观感受,它汇集了由于使用者在不同的环境下工作而造成不同程度的舒适感觉[18]。从舒适性定义出发,助老机器人对老年人伴行舒适性的影响依据老年人手部振动的最大幅值和最大速率的大小来分析。
为了研究助老机器人对老年人伴行舒适性影响,根据以上求得的振动模型,从助老机器人遇到瞬时冲击和地面不平两种情况采用MATLAB/Simulink软件分别对其进行仿真分析。根据助老机器人的物理样机测算,获得助老机器人相关参数如下:
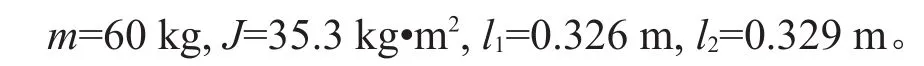
接触刚度、接触阻尼和手部质量参数如下:

2.1 瞬时冲击情况
当助老机器人辅助老年人行走过程中,突然遇到地面上的杂物时,即机器人受到瞬时冲击情况,这时机器人发生振动,进而引起老年人手部的局部振动。为了研究对老年人伴行舒适性的影响,分别从老年人手部水平方向和竖直方向的振幅、振动速度进行分析。
(1)以前轮遇到地面杂物高0.1 m,前轮位移
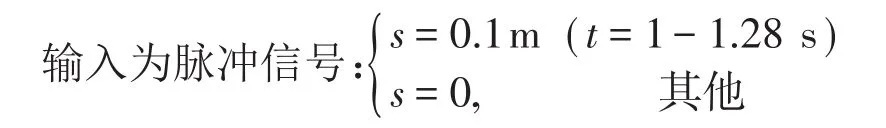
(其中s表示位移,t表示时间);后轮没有遇到杂物,位移输入为s=0(其中s表示位移)为例进行仿真,仿真结果如图4-图7所示。

图4 手部水平方向位移响应曲线图

图5 手部水平方向速度响应曲线图

图6 手部竖直方向位移响应曲线图
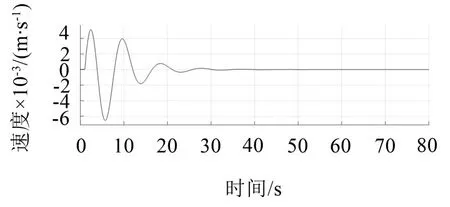
图7 手部竖直方向速度响应曲线图
由图4和图5可以看出,手部水平方向振动的最大幅值为7.5 mm;振动最大速率为9.6 mm/s。由图6和图7可以看出,手部竖直方向振动的最大幅值为9.3 mm;振动最大速率为6.4 mm/s。老年人手部的水平方向和竖直方向振动的最大幅值和最大速率均较小,由此反映出老年人手部的振动强度较小,老年人不会感到不适,也不会引起手麻症状,能够满足老年人的舒适性要求。
(2)以前轮遇到地面杂物高0.1 m,前轮位移

(其中s表示位移,t表示时间);后轮遇到杂物高0.05m,后轮位移输入为脉冲信号:(其中s表示位移,t表示时间)为例进行仿真,仿真结果如图8-图11所示。

图8 手部水平方向位移响应曲线图

图9 手部水平方向速度响应曲线图

图10 手部竖直方向位移响应曲线图

图11 手部竖直方向速度响应曲线图
由图8和图9可以看出,手部水平方向振动的最大幅值为3.8 mm;振动最大速率为4.8 mm/s。由图10和图11可以看出,手部竖直方向振动的最大幅值为14 mm;振动最大速率为10 mm/s。同样,由两方向的振动最大幅值和振动最大速率也反映出老年人手部的振动强度较小,老年人也不会感到不适,也不会引起手麻症状,故能满足老年人的舒适性要求。
2.2 地面不平情况
当助老机器人辅助老年人行走过程中,突然遇到地面不平,在这里,以正弦激励道路为例。即前、后轮位移输入相同,仅存在竖直方向的振动。为分析其对老年人伴行舒适性的影响,同样地从振动幅值和振动速度两参数进行分析。以正弦激励s=0.05sint(其中s表示位移,t表示时间)为位移输入信号为例进行仿真,仿真结果如图12和图13所示。
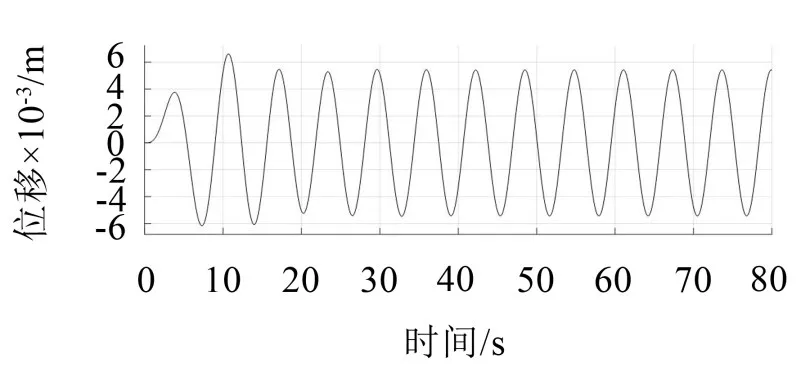
图12 手部竖直方向位移响应曲线图

图13 手部竖直方向速度响应曲线图
由图12和图13可以看出,手部竖直方向振动的最大幅值为6.7 mm;振动最大速率为6.2 mm/s。作与瞬时冲击情况下相同分析,表明其也能满足老年人的舒适性要求。
3 结语
本文给出了助老机器人和老年人手部的振动模型;并通过MATLAB/Simulink软件仿真分析了瞬时冲击和地面不平两情况下,老年人手部在水平和竖直两个方向上的振动情况,得到了不同位移输入信号下,老年人手部振动的最大幅值和最大速率。并在给定实例下,对老年人的舒适性影响进行了分析判断。其研究过程为分析同类助老机器人因路面不平或瞬时冲击对老年人舒适性的影响分析提供了理论基础。
