发动机气门弹簧工艺参数调整

黄伟松，陈 浩，蔡丽红，杨书伟，王以鹏

（上海工程技术大学 汽车工程学院，上海 201620）

气门弹簧是内燃机配气机构中气门组件的重要组成部分，通过弹簧自身张力克服气门关闭过程中气门及传动件因惯性力而产生的间隙，保证气门及时落座并紧密贴合，同时也可防止气门在发动机振动时因跳动而破坏密封[1]。而在实际气门弹簧的生产过程中，无法对废品弹簧进行及时有效的在线判断，造成生产过程中的废品率过高。因此，对于如何在线判断废品、判断废品的依据以及调整工艺参数的依据显得尤为重要。而气门弹簧的节距，是弹簧力学性能的重要参数[2]。同时，也是实际生产过程中需要控制的生产参数。它影响气门弹簧的自由长度，从而直接影响弹簧的力学性能。但是，由于生产工艺的影响，实际生产过程中，弹簧节距值与理论设计值总存在一定的偏差。当超差量在一定范围内时，不会影响到弹簧的合格率，同时能减少生产成本。本文着重分析节距偏差对弹簧总长的影响，建立不同偏差值的弹簧模型，对其进行仿真分析，以获得能保证其使用性能的最大偏差量。

1 气门弹簧的性能要求

气门弹簧的基本参数是弹簧预紧力和弹簧刚度。气门弹簧在疲劳寿命的使用范围内，必须保证弹簧具有规定要求的弹性刚度，提供足够的反力来平衡系统中气门及其相关附件产生的各种力和惯性力，保证气门闭合的力度和避免气门飞脱[3]。同时，必须保证气门弹簧的工作频率和它的固有振动频率不成整数倍关系，防止发生共振，使弹簧发生断裂[4][8]。

气门弹簧的使用过程中，由于受到压缩载荷的作用，会产生并圈现象，这种自接触行为会导致弹簧刚度呈非线性变化。在压应力作用下，气门弹簧会受到沿着45°方向的剪应力作用，最终导致疲劳断裂[5]。因此，设计过程中，必须保证气门弹簧的最大剪应力、米塞斯应力小于许用应力，其1阶模态远远小于工作频率。如下图1所示。

图1 气门弹簧疲劳破坏图

2 弹簧节距与自由长度的数模

在气门弹簧的实际生产过程中，由于伴随着节距误差，弹簧的节距会逐渐增加。因此，弹簧的自由长度也会增加而偏离理论值。为了建立合适的节距——自由长度数学模型，测量了大量的弹簧实际节距，得到以下弹簧自由长度计算公式

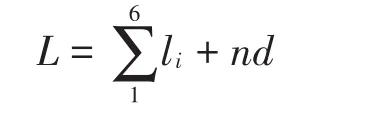
li是气门弹簧在180度位置的实际测量高度，n和d分别表示气门弹簧的圈数和气门弹簧的钢丝直径。测量时，分别测量弹簧上下端面到中面的距离来减少测量误差，然后对这些节距进行数据处理发现：

（1）规定气门弹簧上、下偏差后，每个弹簧的节距值的变化趋势一致。

（2）对于同一个弹簧，相邻的三圈弹簧之间，测量出两个不同的节距值。

3 气门弹簧分析理论及CAD模型

3.1 分析理论

3.1.1 静力学分析理论

气门弹簧的静力分析过程中，忽略了惯性力，及平衡方程中并没有考虑了加速度的影响，因而整个系统控制方程为

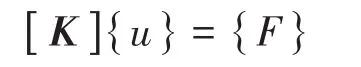
因此，结构静力学问题，即归结为求解静力方程[6]。

3.1.2 模态分析理论

模态分析是分析结构自然频率和模态形状的方法，其在分析中会假设：

（1）结构刚度矩阵和质量矩阵不发生改变；

（2）除非指定使用阻尼特征求解方法，否则不考虑阻尼效应；

（3）结构中没有随时间变化的载荷。

在无阻尼系统中，结构振动方程如下所示

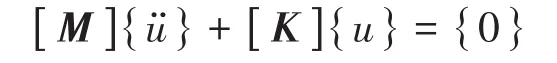
式中：[M]为质量矩阵；[K]为刚度矩阵；{}为节点加速度向量；{u}为节点位移向量。其中刚度矩阵可以包括预应力效应带来的附加刚度[7]。

3.2 气门弹簧CAD模型

实际生产过程中，弹簧的节距与理想的设计尺寸存在一定的误差，因此，理想的弹簧设计模型与实际制造的弹簧模型存在一定的差别。其中，自由长度以及节距的差异性造成了实际生产的气门弹簧与理论设计的弹簧的力学性能的差异。通过建立数学模型，可以发现实际生产过程中，气门弹簧的自由长度超差量分别为正向超差、负向超差。某企业气门弹簧生产过程中，允许的正负值超差量极值均为2 mm。实际生产中弹簧自由长度超差量越大，生产中的废品率越高。为了找到正、负偏差量的极限值，同时验证2 mm的超差量时，生产出的弹簧是否符合要求，分别在两个极限范围内设置不同超差量，实际自由长度超差量数值如表1所示：

根据实际弹簧的节距变化数据找到的数学模型，计算出每一圈弹簧节距相对于标准件弹簧的变化值，建立不同自由长度超差量气门弹簧的CAD模型。气门弹簧标准模型如下图2所示。

图2 标准气门弹簧CAD模型

表1 弹簧模型超差量/mm

4 结果及分析

4.1 标准气门弹簧性能

弹簧实际生产过程中，实际节距与理论值总存在一定的偏差，因此，弹簧的刚度和质量也会随之变化，进而影响弹簧的振动特性。共振将导致配气机构不能正常工作，气门将发生冲击和反跳，共振严重时甚至会导致弹簧断裂。为了保证发动机运转的平稳性和安全性，很有必要对气门弹簧振动特性进行研究，避免发生共振[8]。弹簧自由长度越接近理论设计值时，弹簧力学性能越能满足其工作需要。为了满足弹簧性能要求，必须尽量减小超差值。然而，超差值越小，生产越困难，废品率越高，生产成本越高，必须设置合理的超差值。因此，进行有限元仿真分析，比较超差模型和标准模型的剪应力、米塞斯应力以及弹簧1阶模态的变化趋势。

气门弹簧在实际工况中会受到预紧力的作用，因此，本文在用ABAQUS软件对气门弹簧进行模态分析时采用预应力模态分析。提取最大剪应力、米塞斯应力以及预应力弹簧1阶模态云图。仿真结果表明最大剪应力和米塞斯应力位置在弹簧中圈内表面上，如图3和图4所示，弹簧1阶模态如图5所示。

图3 标准弹簧最大Tresca应力

图4 标准弹簧的米塞斯应力

图5 标准弹簧1阶模态

由仿真结果的中的最大Tresca应力可求出最大剪应力

基于对有限元软件求解结果的分析，得出标准气门弹簧完全满足力学性能要求。完全符合实际的工作状况。

4.2 正偏差气门弹簧性能

对于正向偏差量的弹簧，通过设置自由长度不同超差量，进行有限元分析，求解出每个模型的最大剪应力、最大米塞斯应力以及1阶模态。并与标准件的最大剪应力、米塞斯应力以及1阶模态比较，观察自由长度的变化与各项性能的相对变化趋势。如下图6－图8所示。

图6 弹簧最大剪应力相对变化趋势

通过Oringin Pro绘制弹簧最大米塞斯应力、剪应力以及1阶模态相对标准件弹簧变化趋势图，可以更加直观地分析弹簧的最大米塞斯应力、剪应力以及1阶模态相对于标准弹簧的变化量。

（1）从上图中我们可以看到，气门弹簧偏差值2 mm在许用偏差范围内，气门弹簧的生产过程满足弹簧性能要求。

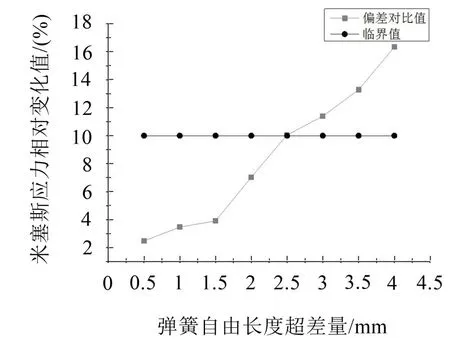
图7 弹簧最大米塞斯应力变化趋势

图8 弹簧1阶模态变化趋势

（2）当弹簧自由长度正向逐渐增大时，弹簧的最大米塞斯应力、剪应力相对标准件弹簧应力值逐渐增大，尽管增大的过程中，有一些小的波动，但主体增长趋势不变。

（3）可以观察到弹簧自由长度变化量达到2.5 mm时，米塞斯应力的变化幅值超过了10%。因此，2.5 mm是偏差临界值。

（4）当弹簧自由长度正向逐渐增大时，弹簧的1阶模态与标准模型1阶模态相比基本不变，超差量对其1阶模态影响不大。

4.3 负偏差气门弹簧性能

对于负值偏差量的弹簧，通过设置不同超差量，进行有限元分析，求解出每个模型的最大剪应力、最大米塞斯应力以及1阶模态。并与标准件的最大剪应力、米塞斯应力以及1阶模态比较，观察自由长度的变化与各项性能的相对变化趋势。如下图9－图11：

同理，通过Oringin Pro绘制弹簧最大米塞斯应力、剪应力以及1阶模态相对标准件弹簧变化趋势图，可以更加直观地分析弹簧的最大米塞斯应力、剪应力以及1阶模态相对于标准弹簧的变化量。

（1）与正偏差结果相似，整体偏差值增大，自由长度也增加，弹簧的最大米塞斯应力、剪应力相对标准件弹簧应力值逐渐增大。

（2）当弹簧的自由长度变化，剪应力相对变化值和米塞斯应力的变化幅值并未超过临界值10%，这表明预设的整体偏差值比较合理。

（3）当弹簧自由长度正向逐渐增大时，弹簧的1阶模态与标准模型1阶模态相比基本不变，超差量对其1阶模态影响不大。

图9 弹簧最大剪应力相对变化趋势

图10 弹簧米塞斯应力相对变化趋势

图11 弹簧1阶模态变化趋势

5 结语

基于实验和仿真研究，本文提出了调整气门弹簧节距的方法，找到合适的偏差值以提高生产质量。其中，有限单元分析法用来确定弹簧整体的偏差预设值。正、负偏差条件下分别计算节距和弹簧整体自由长度的关系。在预设整体偏差条件下，这些规则可以运用于每个节距的调整，从而提高生产质量。建立标准CAE模型和正、负偏差的范围。结果表明：

（1）最大米塞斯应力和剪应力随着自由长度偏差量的增大而增大，气门弹簧1阶模态相对于标准模型的1阶模态变化可以忽略。

（2）与标准弹簧模型相比，弹簧整体长度正偏差量不能超过2.5 mm，设置的所有负偏差量都满足要求。因此，在弹簧制造生产过程中预设2.0 mm的偏差量是符合质量要求的。以后可以进一步实验，对不同规格的弹簧进行研究，得到弹簧自由长度和许用超差量的关系，可以更快捷地得到不同弹簧在制造过程中可控制的超差量，以达到提高生产质量的目的。