基于BDD考虑共因失效的接触网系统可靠性分析*

陈子文， 赵 峰， 陈小强， 王 英

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

0 引言

截至2017年底，我国铁路运行里程已突破12.7万km，其中高铁线路占20%。作为高速铁路列车的直接动力来源，接触网设备长期处于露天环境运行且无备用，是牵引供电系统中的薄弱环节。王列妮等[1]对某路局十年内的事故分布规律进行分析，发现因牵引供电系统故障以及外部环境影响造成的事故占18.78%。因此，加强对接触网状态的检测和可靠性分析对提高高速铁路的可靠性具有重要意义。

对接触网可靠性的研究由来已久，万毅等[2]建立了接触网故障树(Fault Tree,FT)模型并对其可靠性进行了分析以及定量计算；王思华等[3]采用马尔科夫方法在部件可修复的情况下完成了对接触网可靠性的分析；赵峰等[4]将GO-FLOW法应用到接触网系统可靠性分析中，通过建立考虑部件失效率的接触网模型，分析了考虑部件失效率的接触网系统可靠性；王贞等[5]利用可信性理论对天气状态下的接触网可靠性进行了分析。然而，上述研究仅仅是针对接触网部件本身可靠度的分析，未考虑共因失效因素对接触网系统可靠性的影响，使得计算结果与实际运行情况存在误差。

为准确地对接触网系统可靠性进行分析，本文将共因失效理论引入到接触网系统可靠性分析中，接触网系统中共因失效是由环境、设计、人为因素等引起多个不同部件同时故障的失效。传统的共因失效研究方法是通过建立系统的故障树模型，将部件独立失效率与共因失效率分开进行计算，当共因失效部件增加或者系统规模较大时会增加大量的共因失效基本事件，造成故障树的冗长，从而导致难以求解。针对传统共因失效方法的不足，本文提出将基于二元决策图(Binary Decision Diagram，BDD)的考虑共因失效的可靠性分析方法应用到接触网可靠性分析中[6-7]，将忽略共因失效情况下的接触网故障树转化为二元决策图，进而求出系统的不可靠度表达式，然后通过隐式方法转化成考虑共因失效的不可靠度表达式，最终完成对考虑了共因失效的接触网系统可靠性的分析。

1 二元决策图与共因失效

1.1 二元决策图

1.1.1 二元决策图基本概念

二元决策图是1种基于Shannon分解的有向无环图，可以直观地反映函数的逻辑结构。研究表明[8-9]：通过将故障树转化为BDD模型可以快速地求取割集，从而求得系统的可靠度表达式。该方法目前被广泛应用于包含共因失效系统的可靠性分析中。

1.1.2 二元决策图的连接规则

BDD模型中，从顶部向下终点为1的路径上，各输出边为1的节点构成故障树的1个割集，连接规则为：故障树中的“与门”通过1输出，分支用实线进行连接；“或门”通过0输出，分支用虚线进行连接。

1.1.3 故障树向二元决策图的转换

自Sheldon提出BDD模型以来，传统的故障树向BDD转化的常用方法是Rauzy提出的ITE构造法[10]。ITE构造法采用递归思想，使用if_then_else结构，即如果x成立则其概率为A；否则概率为B，其数学达式为：

(1)

从故障树的最底端开始，用底事件将门事件进行置换，由下向上进行转化，每置换一步，按ITE结构对置换进行编码。直到所有的门事件均用底事件进行置换编码，最终得到顶事件的BDD模型。该方法的缺点是进行BDD构造时，需要了解底事件的指标顺序，然而指标顺序需要借助故障树来进行求解，对于结构度复杂的系统计算起来非常繁琐。

为了弥补该方法的不足，本文采用文献[11]中的转换方法：逻辑相邻优先组合法(Logic Neighbor Priority Connect，LNPC)。该方法采用一定的规则从上到下，将故障树快速地转化为BDD模型，转换规则为：

规则1：存在底事件时，如果底事件的位置越高，则对应的优先级越高；底事件重复出现次数越多，优先级越高，如果次数相同则选择第2次出现的位置高低确定优先级；如果底事件在同一层，则左边位置的优先级高。

规则2：存在门事件时，位置越高对应优先级越高；若在相同位置则含有已排序的底事件的门事件优先级高；门事件下底事件少的优先级高；左边的门事件优先级高。

规则3：对于同时有门事件与底事件存在的情况，遵照以下规则进行排序置换：

1)假如门事件中所有底事件都没有排序过，先按底事件的排序规则将底事件进行排序，再按门事件的排序规则对门事件进行排序；

2)假如门事件中的底事件中有已经排过序的，选择包含已排序底事件的门事件优先进行排序。

图1为1个故障树案例模型，以此为例，利用LNPC法进行故障树向BDD模型的转换。

图1 故障树模型案例Fig.1 Fault Tree model case

根据LNPC转换规则可知，底事件的优先级为：X1>X2>X4>X3。通过二元决策图的连接规则可以得到图1故障树的BDD模型，如图2所示。

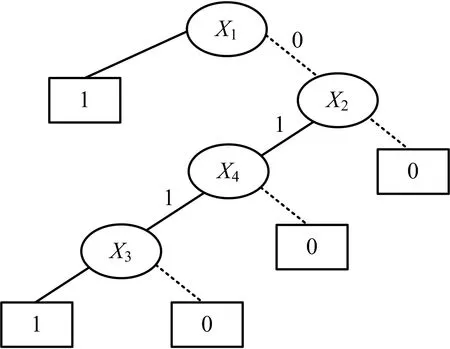
图2 故障树BDD模型Fig.2 BDD model of Fault Tree

1.2 共因失效

1.2.1 共因失效系统的划分

根据承受共因失效冲击单元的数量，可将共因失效类型分为全部单元承受共因失效冲击和部分单元承受共因失效冲击。部分单元承受共因失效冲击是指单元中部分单元受共因失效影响或影响相对比较明显。在进行共因失效的研究中，要明确受影响的单元，否则会使计算结果出现误差，单元考虑不全面时会使计算结果偏向于积极。文献[12]基于贝叶斯网络，利用β因子对接触网可靠性进行了分析，但是对部件考虑的不够全面。

1.2.2 考虑共因失效系统可靠性分析

目前，针对共因失效系统的可靠度计算广泛采用计算量小、分析方便的隐式替代法[13]，具体步骤如下：

1)忽略共因失效的影响，根据系统的不可靠度模型，求出系统的不可靠度表达式，设其为Uc。

2)将受共因失效影响的底事件划分为1个共因失效组，根据共因失效的定义可知，各共因失效组内底事件应具有相同的概率分布，即P1=P2=…=Pn=Pj(t)，在此基础上对步骤1)中的Uc进行化简。

假设在某个具有n个元件的共因组中有j个元件同时失效，且失效过程相互独立，设每个单元的可靠度为Ri(t)(1≤i≤n)，根据最小路集以及最小割集概念，将系统的可靠度Rs(t)表示为单元可靠度Ri(t)的函数，即：

Rs(t)=f[R1(t),R2(t),…Rn(t)]

(2)

假设承受共因失效冲击的n1个单元可靠度相同且为R(t)，不承受共因失效冲击的其他单元采用原有的标号，可以得到系统可靠度表达式为：

Rs(t)=f[R(t),R2(t),…,Ri(t)]

(3)

在隐式方法中，若同一个共因组中每个元件都具有相同的概率，则n个单元组成的共因组中任意1个单元正常的概率为：

(4)

式中：λi(i=1，2，…n)为指定的i个单元同时故障的概率。在n个单元组成的系统中，指定的j个单元同时正常的概率为：

(5)

在相似模型条件下可以进一步化简为：

(6)

2 接触网系统可靠性模型的建立

2.1 接触网系统的划分

复杂功能层次系统一般由功能模块和层次多样的部件组成。对于此类系统，学者更多关注系统在规定的条件与时间范围内其保持正常功能的能力[14]。接触网系统由接触悬挂装置、定位装置、支柱与基础装置、支持装置4大部分组成，接触网系统的故障树模型如图3所示。

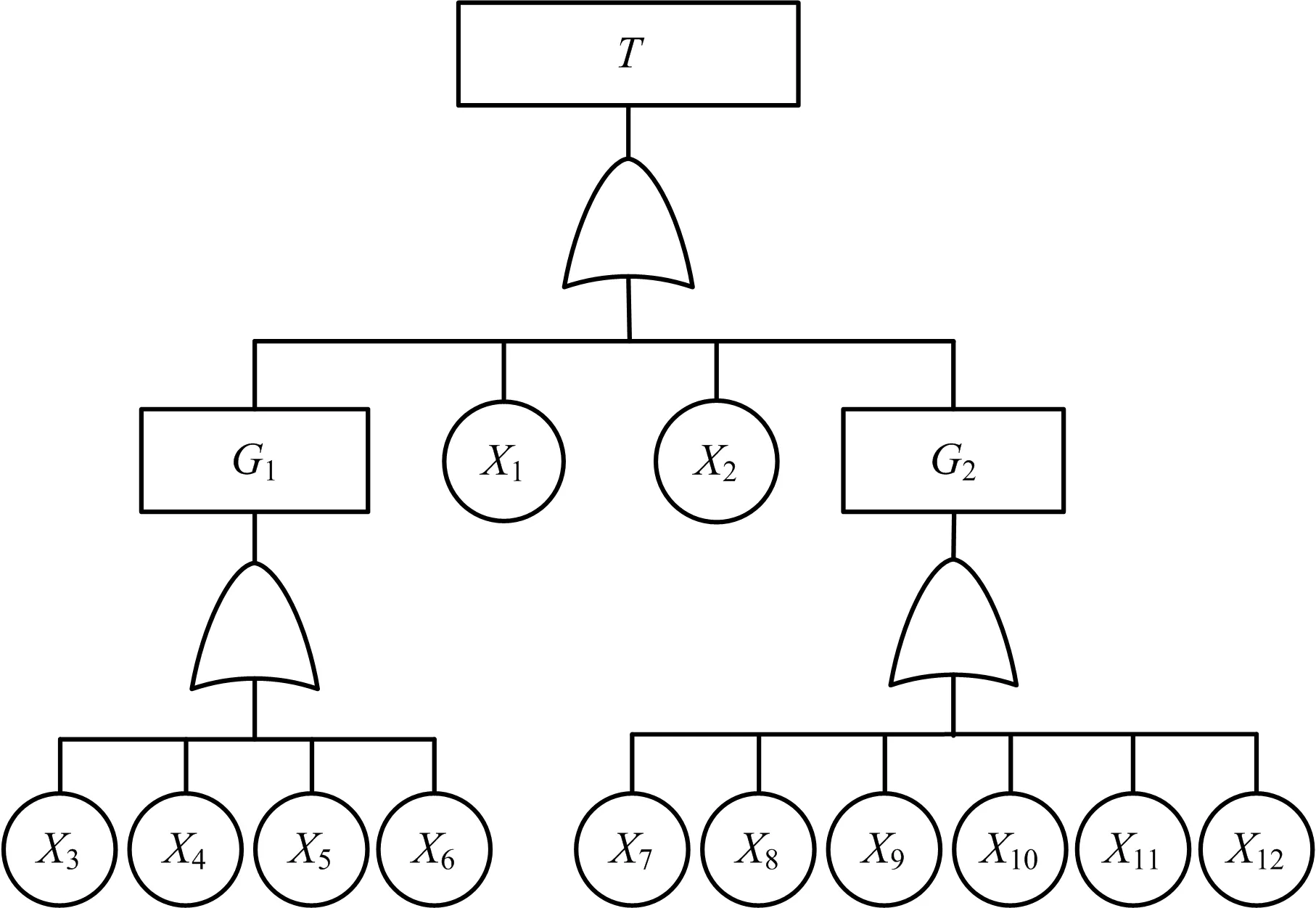
图3 接触网故障树模型Fig.3 Fault Tree model of overhead contact system

由接触网各部分之间的关系可知，接触网系统为1个串联系统，系统中只要有1个部件出现故障，整个接触网系统就会失效。接触网基本事件发生概率是根据调研收集到某段铁路长年的故障统计结果，分析接触网各部件的故障率得到的[15]，如表1所示。

2.2 接触网系统BDD模型

本文旨在研究接触网系统在一定时间内保持正常功能的能力，假定系统刚开始时各部件均处于最佳运行状态，不考虑修复率的影响。

利用LNPC法将接触网系统故障树模型转化为BDD模型。根据排序原则可以得到基本事件与门事件之间的优先级：X1>X2>G1>G2；X3>X4>X5>X6>X7>X8>X9>X10>X11>X12。依据BDD连接规则由图3可得到接触网系统的BDD模型，如图4所示。

通过BDD模型可以很容易得到系统的不交化路集，从X1出发，X12截止，所有指向0的串联系统可以表示为接触网正常工作的组合。

表1 接触网系统各部件故障率Table 1 Failure rate of each component in a overhead contact system

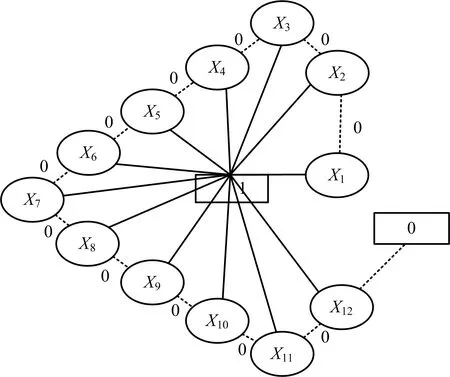
图4 接触网系统BDD模型Fig.4 BDD model of overhead contact system

3 接触网系统可靠性实例分析

3.1 接触网系统共因失效组的划分

对考虑共因失效的接触网系统进行可靠度计算时，根据共因失效的概念以及接触网部件的失效概率，对表1中的部件进行共因组的划分。由于各个部件故障率不同，根据部件的故障率将上述部件划分为3个共因组，假设αi，λi，βi分别表示同一共因组内某几个元件同时失效的概率，共因失效组的划分如表2所示。

设某共因失效组中i个单元同时失效的概率为λ1=0.035 7，λ2=0.02，α1=0.043 5，α2=0.04，α3=0.003，α4=0.002，β1=0.13，β2=0.065。

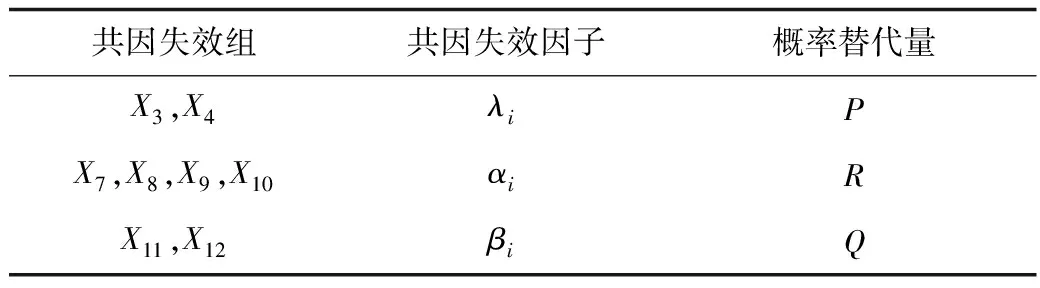
表2 接触网共因失效组划分Table 2 Division of CCF cuts on catenary

3.2 考虑共因失效的接触网可靠度计算

根据图4内容，结合1.2.2步骤1)和2)，可以得到在未考虑共因失效情况下接触网系统的可靠度为：

(7)

由1.2.2步骤3)可知，在考虑共因失效情况下接触网系统的可靠度为：

(8)

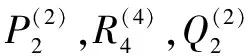
将数据代入公式(8)，可得在考虑共因失效的情况下Rs(t)为：Rs(t)=1-exp(-(5×t)/4)×exp((3×t)/25)×exp((6×t)/25)×exp(t/50)×exp(-(13×t)/50)×exp(-(13×t)/200)×exp(-(107×t)/250)×exp(-(87×t)/500)×exp(-(107×t)/500)×exp(-(357×t)/5 000)×exp(-(943×t)/10 000)×exp(-(357×t)/20 000)。

利用MATLAB绘制函数Rc(t)与Rs(t)随时间变化的曲线，考虑到接触网实际维修时间，时间t取值范围为0～1 a，如图5所示。

图5 接触网可靠度对比Fig.5 Comparison of reliability of catenariy

由图5可以看出，接触网系统可靠度在1 a内随运行时间的增加越来越差。考虑共因失效时接触网系统的可靠度变化更加明显，t=0.5 a时Rc(t)为0.333 8，Rs(t)为0.287 7，两者相差13.8%，说明在对接触网系统进行可靠性研究时需要考虑共因失效的影响。

4 结论

1)将接触网故障树模型转化为BDD模型可以快速得到接触网系统的可靠度表达式，简化考虑共因失效的可靠性分析过程，为接触网可靠性分析提供了理论依据。

2)对比未考虑共因失效的接触网可靠度，在融合了共因失效后接触网可靠度下降较明显，因此，在对接触网进行设计以及设备选择安装上需要考虑共因失效的影响。