基于SAPSO-BP网络模型的海洋平台落物碰撞损伤分析*

2019-03-05周世博章文俊李泽华尹建川

中国安全生产科学技术 2019年2期

周世博，章文俊，李泽华，尹建川，黄腾

(大连海事大学航海学院，辽宁大连 116026)

0 引言

在海洋平台作业中，物体意外坠落可能对海洋平台结构完整性和海底管线产生严重损害，根据DORIS统计，落物是海洋平台意外事故中排名前十的重大事故之一[1]。随着海洋油气工程的快速发展，海洋平台作为石油开采的基础设施，供给船和平台之间的吊装作业频率也随之增高，吊机落物的意外事故时有发生。在海洋平台的各种吊装作业中，每个平台作业年五分之一的事故是钢管在吊装作业中发生坠落[2]。重大件物体(如BOP、集装箱、钻头、立管等)的坠落会对海洋结构物、海洋平台甲板甚至海底管线造成损害，有时还会造成人员伤亡和环境污染。因此，对海洋平台落物碰撞过程进行仿真模拟分析十分必要。国内外关于海洋平台物体坠落的研究，主要以实验法、软件仿真、解析计算法3种方法应用较为广泛。Heo[3]基于三维管道保护系统，用LS-DYNA仿真分析得到每个选定跌落对象场景的结构效应，提出了落物风险分析计算结构失效概率的算法；Alghamdi[4]研究了可折叠碰撞能量吸收器以及不同形状管的变形模型；Arabzadeh等研究了在横向载荷条件下受压管道的动力响应。近年来，关于海洋平台落物碰撞的研究主要集中在落物碰撞的位置、落物的质量等。

本文以某平台为例，运用数值仿真分析的方法，研究了坠落立管以不同角度撞击海洋平台甲板的响应过程。运用ANSYS/LS-DYNA有限元软件进行碰撞过程的显示动力学分析，仿真得到了平台甲板结构损害变形结果、凹陷变形程度、最大等效应力等。

人工神经网络能够进行复杂的、非线性、非平稳性的系统仿真分析。海洋平台落物碰撞具有严格的非线性、随机性和局部性的特点，本文运用自适应粒子群优化算法，结合了PSO算法的全局搜索最优能力和自适应变异算法跳出最优解的能力，使得BP网络模型能够迅速跳出局部最优，快速找到全局最优解。对海洋平台落物碰撞损伤进行了分析计算，并和仿真结果进行了对比，发现SAPSO-BP网络模型具有更精确的碰撞损伤分析结果。

1 碰撞问题显示动力学分析

落物指有可能导致死亡、伤害或设备/环境破坏的任何物体由于自身重力从初始静态位置跌落，本文的落物指海洋作业中的坠落物体。落物和海洋平台甲板之间的接触是典型的冲击碰撞问题。因为涉及到高度的非线性，使得落物碰撞的问题在一定程度上变得复杂。就跌落碰撞问题而言，有2种方法可以用于分析研究，一是实验法，二是有限元分析法，最常见有效的方法是有限元法[5]。随着CAE的发展日趋成熟，特别是非线性有限元技术的成熟，显示有限元数值仿真技术更多地被应用于跌落碰撞的研究中。因此，本文运用ANSYS/LS-DYNA进行了显示动力学分析。落物碰撞的方程为：

(1)

(2)

在LS-DYNA显示动力学分析中采用中心差分法，在碰撞系统中的各个节点在第n个时间步结束(即tn时刻)的加速度矢量为：

(3)

根据中心差法的思路可知，速度的一阶差分表现为加速度，位移的一阶差分表现为速度[6]。可以得出tn+1时刻的速度和位移：

(4)

(5)

式中时间步长是由时间步开始和结束的时间点定义的：

Δtn+1=tn-tn-1,Δtn=tn+1-tn

(6)

(7)

对碰撞问题进行动力学分析，根据时间积分法可分为显式和隐式求解方法。此处选择显示求解法进行计算分析，因为显示算法对于解决变形问题和高度非线性问题具有更大的优势[7]。ANSYS/LS-DYNA具有显示动力学分析模块，是解决碰撞问题的有效工具之一，仿真流程如图1所示。

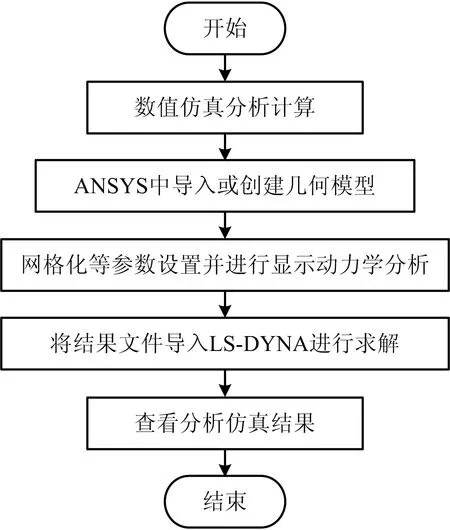
图1 ANSYS/LS-DYNA数值仿真流程Fig.1 Numerical simulation flow chart of ANSYS/LS-DYNA

2 数值仿真分析

以某海洋钻井平台为基础，运用ANSYA建立有限元落物碰撞模型，落物撞击到海洋平台甲板的部分位置。以海洋平台甲板为研究对象，选取碰撞区域部分甲板尺寸为10 m×80 m，甲板厚度0.03 m，桁材间距为3.1 m。所有部件的弹性模量E=206 GPa，泊松比μ=0.3，密度ρ=7 850 kg/m3。钻井立管长10 m,外径(OD)0.476 3 m，内径(ID)0.431 9 m。立管坠落的垂向初速度是0.06 m/s，重力加速9.81m/s2，研究分析甲板结构的承受能力和安全强度范围。碰撞角度为90°和45°坠落的有限元模型如图2～3所示。

图2 碰撞角度为90°的立管坠落有限元模型Fig.2 The finite element model of dropped riser with impact angle 90°

选择不同工况组合进行ANSYS/LS-DYNA模拟仿真实验，模拟实验设计方案如表1所示。图4～5为在碰撞角度为90°和45°时的应力分布图。

图3 碰撞角度为45°的立管坠落有限元模型Fig 3 The finite element model of dropped riser with impact angle 45°

可以看出，冲击损伤局部化且基本集中在碰撞接触区域。在撞击过程中，相当数量的能量转化为平台的动能，碰撞后引起甲板凹陷，动能转化为甲板的弹性应变和塑形应变，最终转化为内能和沙漏能等其他能量。一方面由于物体相对于海上平台的冲击能量小；另一方面，整体平台具有良好的弹性变形能力[8-10]，可以减少坠落物体对结构损伤的影响。

表1 仿真模拟设计组合Table 1 The design combination of Simulation

图4 碰撞角度为90°时应力分布Fig.4 The distribution cloud at impact angle of 90°

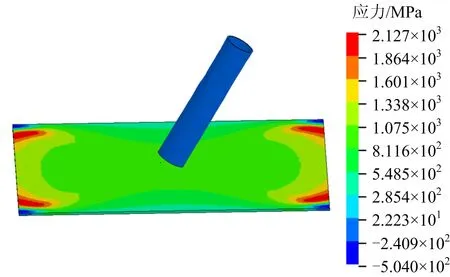
图5 碰撞角度为45°时应力分布Fig.5 The distribution cloud at impact angle of 45°

3 坠落立管碰撞结果分析

很多坠落事故是由起重设备吊装作业过程中人员操作不当及海上环境影响导致的。在此情况下，坠落物体与平台甲板会成一定的角度，所以对不同的撞击角度的碰撞后果进行了仿真研究。对于整个碰撞系统，总能量由下落物体的初始动能提供，质量和速度决定下落物体的初始动能，坠落物体的角度也不容忽视。从仿真结果可以看出，其他条件保持一致的情况下，垂直下降立管引起的应力分布比其他角度引起的应力分布更为集中。最大等效应力越大，甲板凹陷程度越严重，甲板结构严重损坏会导致甲板破裂，结构失效。当坠落立管水平坠落(碰撞角度为0°)时，甲板受到的冲击损伤较小，在海洋平台甲板结构的安全承受范围之内。最大等效应力变化和甲板凹陷深度随碰撞角度的变化分别如图6和图7所示，甲板受到冲击碰撞的应力和凹陷深度随着碰撞角度的增大而增大，碰撞角度为85°～90°时，即与竖直方向偏移5°～10°时，甲板凹陷程度最大，出现破裂，结构失效。

图6 最大等效应力变化Fig.6 The change of the Maximum equivalent stress

图7 甲板的凹陷深度变化Fig.7 The depth change of deck depression

其他条件相同的情况下，物体下落的冲击角度越大，结构能量吸收的弹性能量比例越大，说明结构以塑性变形的形式吸收了更多的能量。非线性动力分析[11]结果表明，平台甲板的结构能承受立管一定程度的冲击，防止立管继续下落造成下部设备和人员受损。此外，考虑到铺设垫层和橡胶垫的钻台平台对立管下落的缓冲，假设立管是1个刚体模型，动量完全被甲板的局部结构吸收且动能被转换为相应的势能[12]。甲板结构设计符合条件下的防坠落要求。

将实验与模拟结果结合可知，坠物与竖直方向偏移5°～10°时，穿透甲板后的位移最大，对甲板下方结构的威胁最大，撞击后果最严重。且DNV海洋平台规范中规定，海上作业设施受坠物撞击时，需计算竖直方向成5°或10°撞击角度的情况，因此建议定义坠物5°～10°为最危险工况并计算。

4 基于SAPSO-BP网络模型拟合

粒子群优化算法(PSO算法)的寻优收敛速度很快，但是也存在着在寻找最优解的过程中早熟收敛、搜索的准确度低、循环后期迭代效率较低等缺点。SAPSO-BP网络模型仿照遗传算法GA(Genetic Algorithm)中的变异操作，在PSO算法中加入了变异算子，对随机变量再一次重新初始化。缩小了种群的搜寻空间，在寻找最优粒子之前得到最优的位置，迭代寻优增加了算法找到最优解的概率。自适应粒子群优化算法实质上是在每次粒子迭代更新之后，将迭代更新后的粒子再以一定的概率进行随机初始化[13]。PSO算法的步骤为：初始化粒子群的速度矢量和位置矢量；计算每个粒子位置对应的适应度值，根据适应值的大小判断解的优劣；根据适应度的大小寻找个体极值和群体极值；更新粒子的速度和位置。粒子群更新公式为：

(8)

式中：w为惯性权重；d=1,2…n;k为当前迭代次数；Vid为粒子的速度，m/s；c1和c2为非负的常数，称为加速度因子；r1和r2为分布[0,1]之间的随机数。自适应变异算子公式为：

pop(j,pos)=λrands(1,1),if rand>c

(9)

式中：j为粒子群的规模；pos为离散的均匀随机正整数；λ为粒子群位置的最大值；c为正常数，通常小于1。

种群在迭代进化的过程中，每个粒子都有1个适应度函数值，以一定的速度通过跟踪个体和群体极值来更新自己的位置，寻找到属于自己的最优值。自适应优化算法以一定的概率初始化迭代更新后的粒子，迭代寻优使误差递减速率加快[14]。适应度函数的方程为：

error=|Yk-Ok|

(10)

式中：Yk为网络模型的预测输出值；Ok为网络模型的实际输出值。种群迭代进化过程中的最优个体适应度函数值变化如图8所示。可以看出，SAPSO-BP混合预测模型的适应度函数值明显小于PSO-BP模型，能够快速搜索到最优的结果。

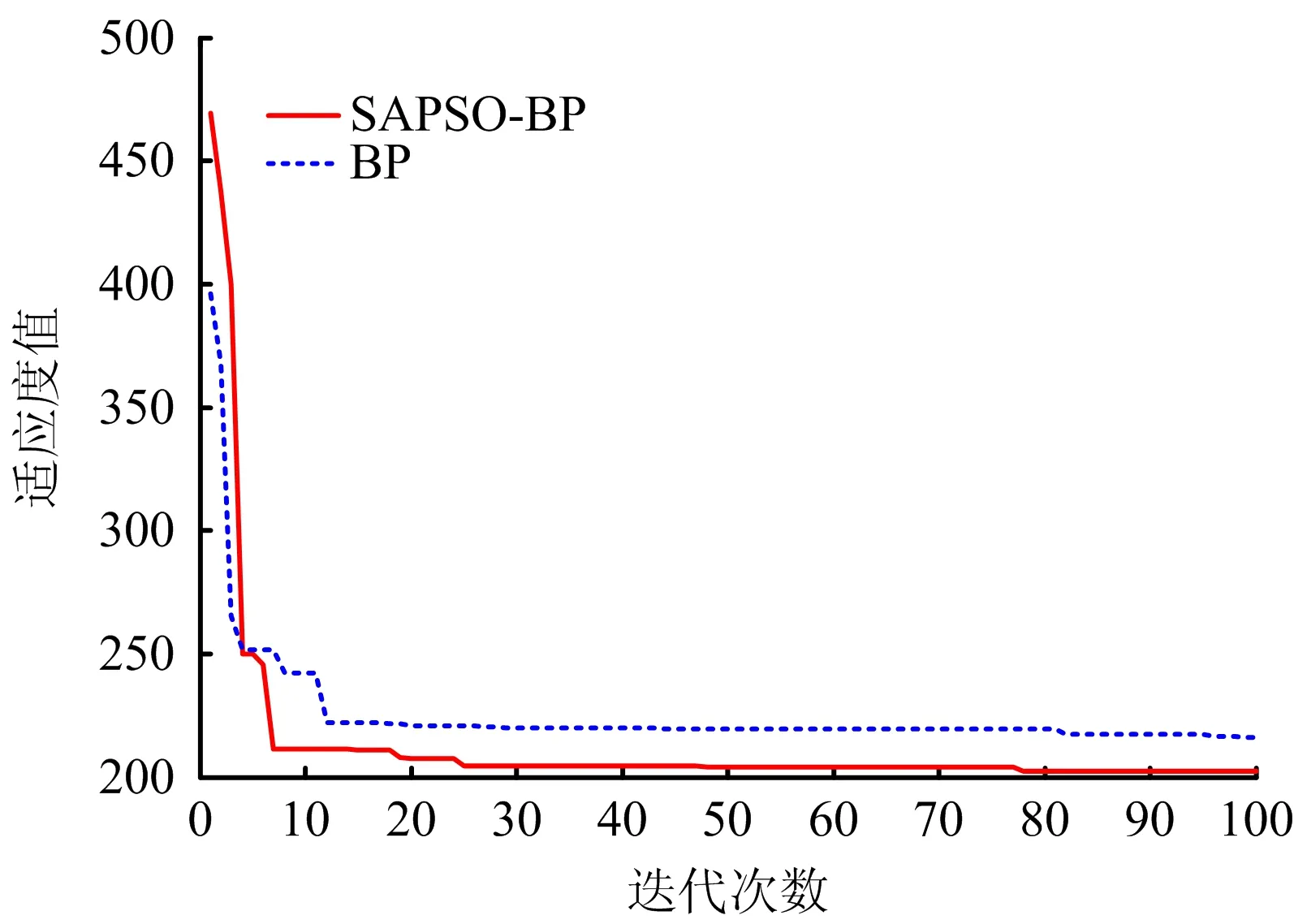
图8 种群适应度函数曲线比较Fig.8 The fitness curve of population

回归分析是1种处理变量统计相关性的数学统计方法。回归分析主要解决以下问题：确定变量之间是否存在相关性，如果有则找出适当的数学表达式；根据1个或多个变量的值，预测或控制另1个变量的值，且可计算预测或控制的准确度。

海洋平台落物方式具有多样性，碰撞角度也具有随机性，碰撞过程具有高度的非线性。根据神经网络的特点，神经网络是1个非线性系统，任意复杂的非线性函数都能够实现良好的逼近。由于BP网络具有收敛速度慢和容易陷入局部极值的缺点，为了提高BP网络拟合的准确性，采用了1种自适应粒子群优化算法——SAPSO-BP优化BP网络[15-16]。

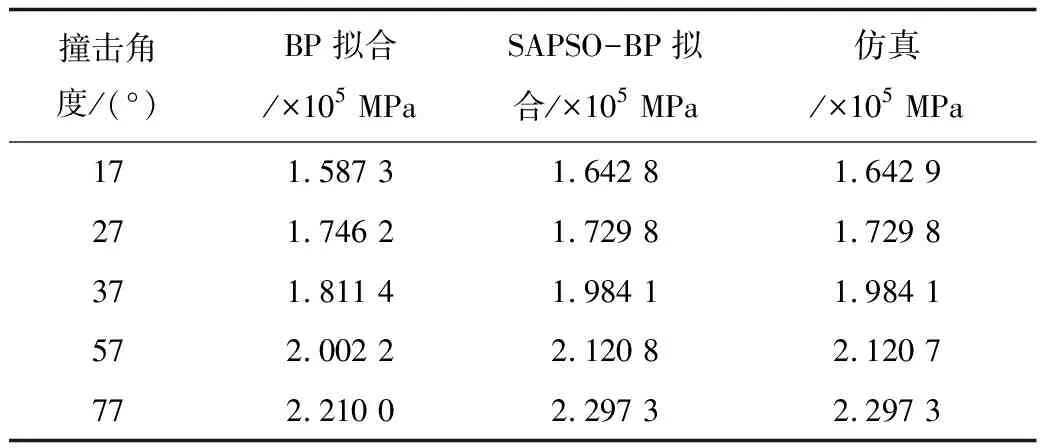
图9和图10分别为海洋平台甲板在不同撞击角度下的应力与凹陷深度的拟合值。从图9～10可以看出，最大冲击力及甲板凹深与冲击角度呈非线性关系，随着碰撞角度的增大呈现增大的趋势。拟合曲线能很好地反映数据分布，可以看出新的自适应粒子群优化算法更加合理高效地提高了BP神经网络的拟合能力。本文选择了另外5个碰撞角度来验证拟合结果，BP拟合和SAPSO-BP网络的拟合结果如表2所示。

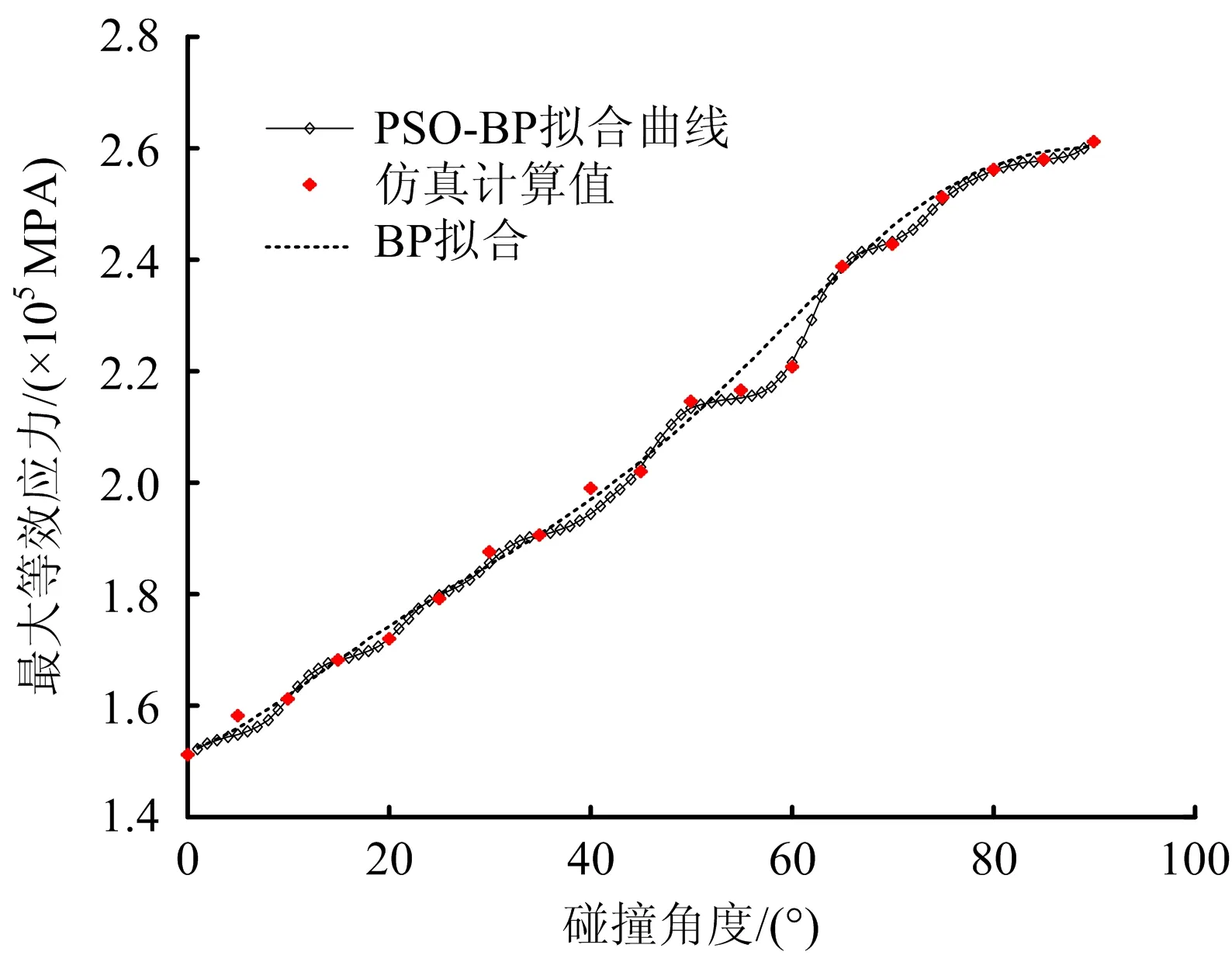
图9 最大等效应力与撞击角度关系的非线性拟合Fig.9 The nonlinear fitting of the relationship between maximum equivalent stress and impact angle

图10 甲板凹陷深度与撞击角度关系的非线性拟合Fig.10 The nonlinear fitting of the relationship between the deck depressions and impact angle

撞击角度/(°)BP拟合/×105 MPaSAPSO-BP拟合/×105 MPa仿真/×105 MPa171.587 31.642 81.642 9271.746 21.729 81.729 8371.811 41.984 11.984 1572.002 22.120 82.120 7772.210 02.297 32.297 3

从表2可以看出，SAPSO-BP算法验证了优化BP网络的有效性和适用性。如碰撞角度为37°时， SAPSO-BP神经网络的拟合结果为19 841 MPa，BP拟合的结果为181 114 MPa，仿真计算结果为19 841 MPa，SAPSO-BP神经网络拟合结果明显优于BP拟合结果。另选取多组数据对比发现，SAPSO-BP拟合曲线的拟合精度较高，能很好地反映最大等效应力与撞击角度之间的非线性关系。自适应粒子群优化算法用来拟合非线性函数减小了拟合误差，模拟结果更稳定，提高了拟合精度[17-18]。