基于蒙特卡洛方法的着陆擦机尾风险预测*

汪 磊，杨星月

(中国民航大学 飞行技术学院，天津 300000)

0 引言

飞行数据显示，民机的进近和着陆阶段是整个飞行过程中的事故高发阶段。虽然着陆阶段仅占整个航段飞行时间的1%，但却有23%的事故和17%的死亡人数[1]发生在这一阶段。其中，擦机尾是一类频发的民航不安全事件，一般定义为飞机起飞或着陆时机尾与跑道道面发生接触的现象，着陆阶段比起飞更容易发生。1991—2013年我国民航共发生擦机尾事件54起，其中着陆阶段发生的擦机尾占52%[2]。飞机在着陆过程中，由于上仰角过大，机身离地面没有足够的裕度，导致机尾擦地。一般来说，着陆俯仰角越大，擦机尾发生的可能性越高。飞机擦机尾很少直接造成机毁人亡，初始阶段只是增加航班运行和飞机维修的成本, 但其对飞机结构的隐形损伤却是不容忽视的，极有可能在一段时间之后成为飞行重大安全隐患之一。

目前，国外学者对擦机尾的研究主要从告警装置设计及风险监测方面开展：Theriault等[3]研发了1种基于图形化警告来提高飞行员警觉性的擦机尾事件目视警告系统；Chan[4]运用天气预报(NWP)模型研究了风切变对飞机擦机尾的影响；Kevin等[5]研制出1种直升机计算机程序来提醒飞行员避免擦机尾。国内学者则对擦机尾的定性原因分析和维修研究较多：郭焕军等[6]分析了空客飞机起飞和着陆2种情况下擦机尾的原因；舒平等[7]对飞机起飞阶段擦机尾事故进行分析并提出预防措施；毛吉星[8]就波音737飞机机尾擦地的损伤进行级别划分并制定对应的维修方案；孙瑞山等[9]利用K-S检验模拟飞机起飞擦机尾离地仰角值的可能分布，并计算具体机队擦机尾事件的风险概率，但选择的样本较少，计算的擦机尾风险的准确性有待提高。

航空公司一般根据飞机着陆时的俯仰角大小来判断飞机是否擦机尾，当着陆俯仰角达到某个特定值时，就会被判定为超限。为了深入挖掘接近擦机尾超限事件的俯仰角数据，利用蒙特卡洛模拟方法，突破样本数据不足的障碍，对飞机着陆时擦机尾的风险进行准确预测。

1 蒙特卡洛方法与飞机着陆擦机尾事件

蒙特卡洛方法[10]是1种通过生成合适的随机数并在已知概率分布中进行抽样模拟试验的统计方法，适用于所有随机事件的模拟计算，在科学技术、经济管理、石油、金融等领域都有广泛的应用，其优点在于能准确地反映不确定性因素的影响，通过对有限的样本数据进行扩充实现对已知问题的求解。蒙特卡洛模拟分析的一般步骤如下[11-14]：

1)建立需要分析概率统计的原始数据模型；

2)产生符合给定概率分布的随机值；

3)运用随机抽样的数据计算具体的估计量；

4)统计分析并绘制相应的图表。

在整个着陆阶段，造成飞机着陆擦机尾的原因有：过早收油门；对油门和速度监控不够；接近地面时下降率太大；高度判断不准确，拉平过高；为了避免重着陆而平飘长；复飞时机晚，加油门不果断。

以Boeing737-800(以下简称B737-800)飞机的着陆阶段为例, 飞机从15.24 m(50 ft)高度以正常的运动轨迹、速度和正确的配平飞行，在主起落架高于跑道6.1 m(20 ft)时，逐渐增加俯仰姿态约2°～3°后开始拉平，减小飞机的下降率。开始拉平后，柔和地将油门杆收至慢车位，使飞机以正常的速度、方向和姿态在跑道入口前304.7～609.6 m(1 000～2 000 ft)处平稳接地。

快速存取记录器 (Quick Access Recorder，QAR)数据是航空公司有针对性地对飞行员进行飞行训练并提高航班运行品质和安全水平的重要依据。对QAR数据超限事件进行统计、分析并据此开展训练已经成为航空公司主要的飞行安全保障手段。

B737-800机型的QAR设备1s内可连续记录4次飞机着陆俯仰角的度数，如表1所示。

目前，国内已有学者利用QAR数据对飞机重着陆风险进行评估预测，但其采集的航班数据有限，评估重着陆风险有一定的局限性。因此，本文根据某航空公司飞行品质监控标准，将6.1 m(20 ft)离地高度至前轮接地所记录的QAR数据作为样本数据，并结合蒙特卡洛模拟方法，解决样本不足的问题，建立擦机尾风险预测模型，为航班擦机尾风险预测提供参考。

表1 QAR原始数据示例Table 1 Example of QAR original data

2 基于蒙特卡洛模拟方法的擦机尾风险预测模型

2.1 建立擦机尾风险评价模型

风险一般指某种特定的危险事件(事故或意外事件)发生的可能性与其产生的后果的组合。通过风险的定义可以看出，风险是由2个因素共同作用，一是危险发生的可能性，即危险概率；二是危险事件发生后所产生的后果。简单来说，风险可表示为某种不利事件或损失发生的概率及其后果的函数，即R=(P,S)。其中：R为风险；P为不利事件或损失发生的概率；S为不利事件或损失发生的可能性。飞机擦机尾风险评价模型可表示为擦机尾发生的可能性与擦机尾发生后导致的严重度的乘积，即：

RPA=PPASPA

(1)

式中：RPA为飞机擦机尾发生的风险值；PPA为擦机尾发生的可能性；SPA为擦机尾事件的严重度。

2.2 随机变量的抽样模拟

2.2.1 正态分布随机数的产生

研究[15]中对飞行QAR数据的大样本统计发现：大部分飞行性能参数，如接地垂直载荷、着陆接地距离、接地仰角等，在较大的样本空间(n>100)里都近似呈现正态分布。基于此，用蒙特卡洛模拟方法生成服从正态分布的着陆俯仰角随机度数，并依据相应的算法预测擦机尾的风险值。用蒙特卡洛模拟方法生成的随机数序列在本质上不是随机的，只是很好地模仿了随机数的性质，但是如果随机数满足分布均匀性、随机性和独立性，并且能满足实际问题的需要，此伪随机数可以同真正的随机数一样使用。

2.2.2 抽样模拟

抽样是在某个随机变量已知的情况下，通过取随机数，实现该变量不断取值的过程。满足正态分布的随机数生成算法很多，Box-Muller变换算法相对便捷、有效，因此，在获得均匀分布随机数的基础上进行Box-Muller变换, 公式如下：

(2)

式中：α为飞机着陆俯仰角的随机度数，(°)；μ和σ分别为已知正态分布样本数据的均值和标准差；r和t为在(0,1)值域内服从均匀分布的独立随机数。

2.3 样本数据及生成的随机数的正态分布检验

1)计算均值和方差：

(3)

(4)

(5)

(6)

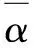
2)假设该样本数据符合正态分布，则对其进行正态检验，若结果表明样本数据符合正态分布，再对其进行方差修正得到总体方差进行无偏估计：

(7)

(8)

3)由此可得该机型着陆时离地俯仰角的分布密度函数：

(9)

使用以期望值为对称轴、α为矩形的区域概率PPA表示飞机擦机尾发生的可能性，如图1所示 。

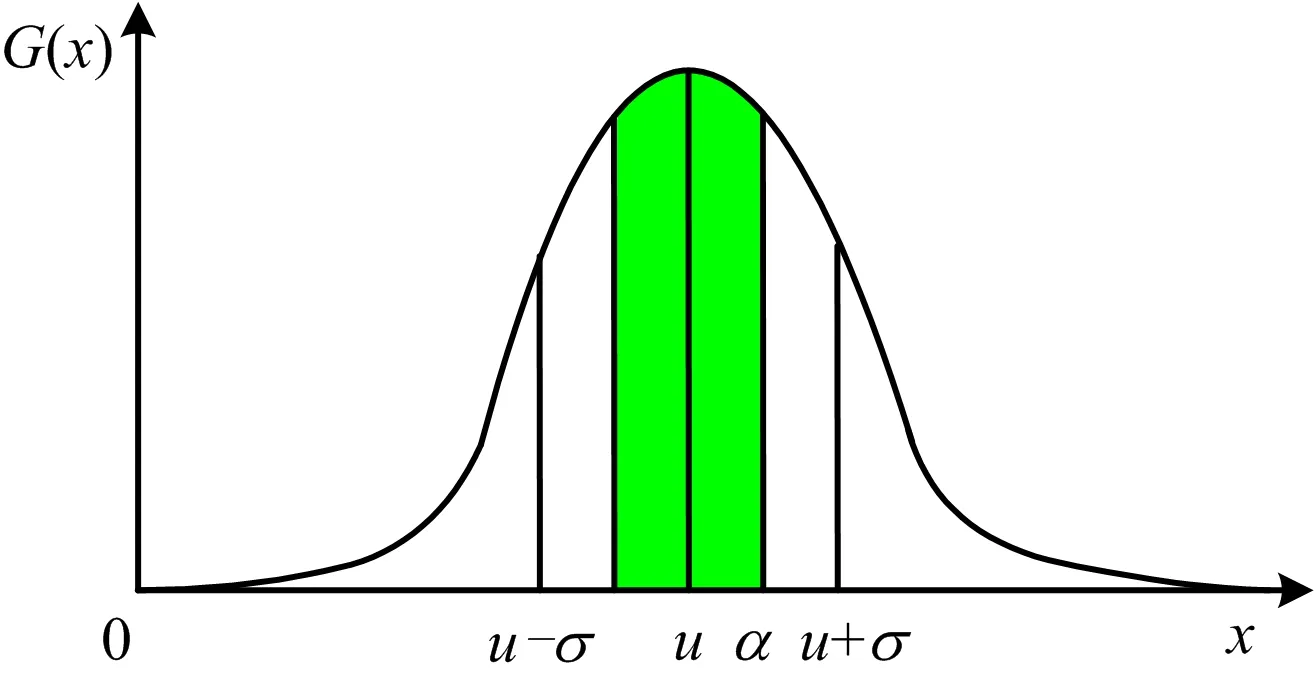
图1 擦机尾参数的正态分布Fig.1 Normal distribution of tail strike risks

通过飞机着陆俯仰角与其分布期望值的关系来判断擦机尾的风险，α越靠近期望值说明擦机尾发生的可能性越小，运用蒙特卡洛模拟方法对飞机着陆俯仰角样本进行扩充，运用式(1)对擦机尾风险值进行具体化计算，可得较准确的风险预测模型。因此，PPA的计算公式可表示为：

(10)

式中：0≤PPA≤1，以样本数据偏离均值的程度来表示飞机擦机尾事件的严重度，离均值越远则严重度越高，计算公式如下(SPA≥0)：

(11)

2.4 擦机尾风险值的评估与预测

抽样得到飞机着陆俯仰角在一定范围内的随机度数α1,以风险评价模型RPA=PPASPA为例,式中参数PPA和SPA的分布如式(10)、(11)所示，则对于每个预测擦机尾风险值的估计值可由式(12)得出。飞机擦机尾风险预测值的表达式为：

(12)

式中：r和t为服从(0，1)分布中相互独立的随机数；μ和σ分别为已知机队样本数据的均值和方差。

2.5 蒙特卡洛模拟流程

在上述预测模型基础上，运用MATLAB编程进行抽样模拟试验，系统运行5 000次，可得到5 000个擦机尾风险预测值。蒙特卡洛模拟步骤如下：

分别取(0,1)分布上2个互相独立的随机数r和t，计算得到着陆俯仰角α1；将α1代入飞机擦机尾发生的可能性与后果的严重性计算公式中，得到PPA1和SPA1；将2个值相乘得到擦机尾风险预测值，完成了1轮抽样。依次进行，如进行5 000次抽样，便有5 000个擦机尾风险值R1，R2，…，R5 000。以着陆的随机俯仰角度数为横坐标，预测的风险值为纵坐标，进行统计整理得到擦机尾风险的分布。模拟流程如图2所示。

图2 蒙特卡洛模拟流程示意Fig.2 The flow diagram of Monte Carlo

3 实例分析及模型验证

本研究将某航空公司B737-800机队的380套QAR数据作为样本数据，其中采集机队1共150个航班，机队2共230个航班，运用MATLAB编程处理共380个航班的数据，得出2个不同机队着陆时俯仰角的频率分布直方图，见图3～4。

图3 机队1着陆俯仰角值的频率分布Fig.3 Histogram of the landing pitch attitude distribution of the first fleet group

图4 机队2着陆俯仰角值的频率分布Fig.4 Histogram of the landing pitch attitude distribution of the second fleet group

由图3～4可知，机队1着陆俯仰角均值为4.340 2，机队2着陆俯仰角均值为4.317 7，整个机队着陆俯仰角均值为4.377 7；机队1着陆俯仰角方差为0.335 6，机队2着陆俯仰角方差为0.332 6，整个机队着陆俯仰角方差为0.342 8。

利用Box-Muller变换随机生成5 000个着陆俯仰角度数，得到2个机队着陆俯仰角随机度数的分布直方图，见图5～6。

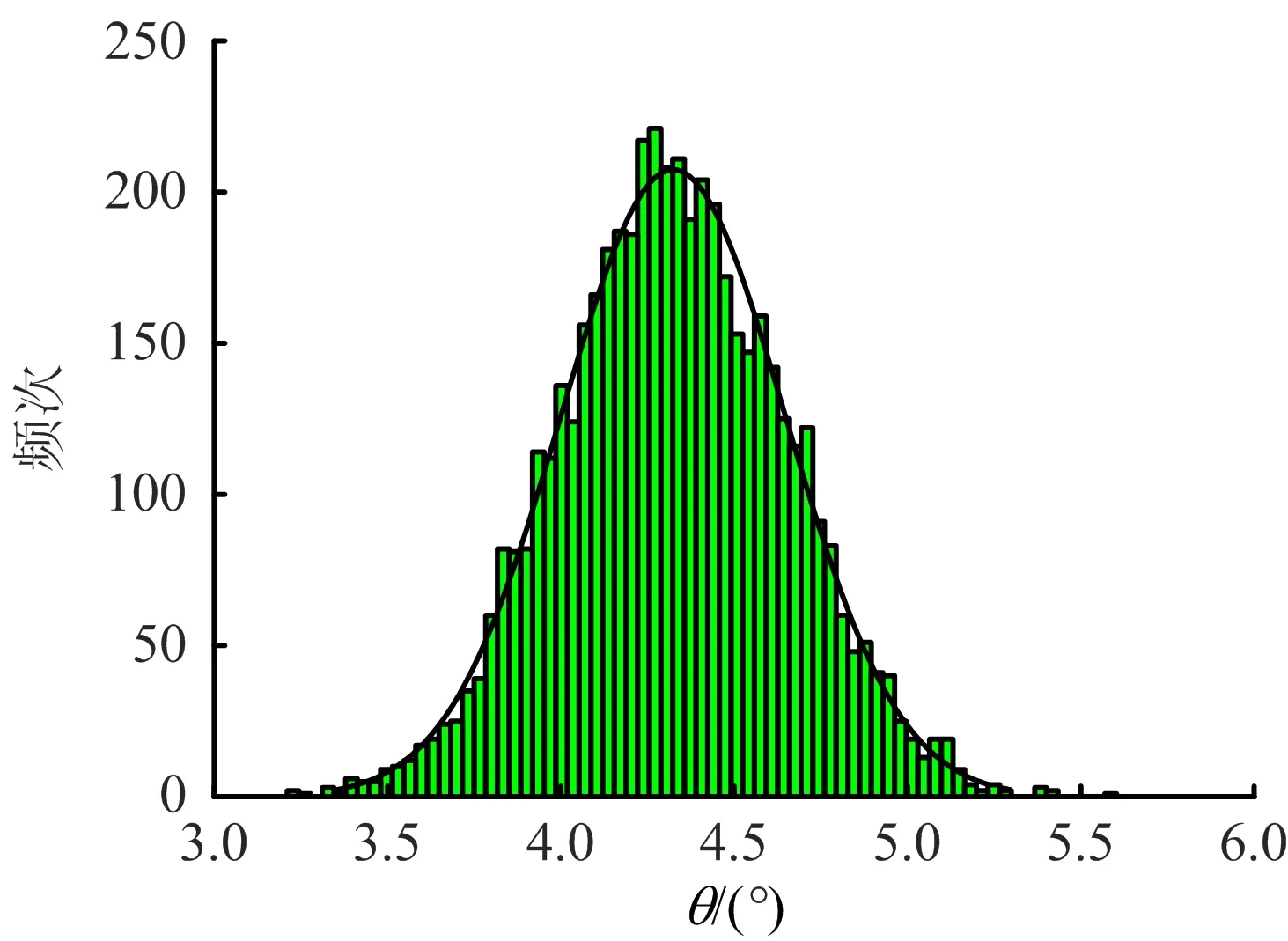
图5 机队1随机生成的着陆俯仰角度数分布Fig.5 The random-generated landing pitch attitude distribution of the first fleet group

图6 机队2随机生成的着陆俯仰角度数分布Fig.6 The random-generated landing pitch attitude distribution of the second fleet group

着陆俯仰角数据抽样模拟之后，标准差数值由0.576 7变为0.558 1，说明蒙特卡洛模拟后的数据更加集中，验证了模拟后的数据质量得到进一步提高，增加了风险预测的可靠性。

取机队2着陆俯仰角的实际数据与每组拟合数据值的差值，取绝对值计算相对误差(相对误差=绝对误差÷实际值)为4.512 3，相对误差的平均值为0.265 4，同理可得蒙特卡洛模拟后相对误差的平均值为0.111 8，说明了蒙特卡洛模拟后数据更准确、稳定。

图7 不同机队擦机尾风险预测曲线Fig.7 The tail strike prediction curve of different fleet groups

对样本进行Kolmogorov-Smirno(K-S)检验，结果符合正态分布。利用擦机尾风险公式，计算随机生成的每个着陆俯仰角对应的风险值，以着陆俯仰角为横坐标，擦机尾风险值为纵坐标,得出不同机队飞机擦机尾的风险预测曲线，见图7。图7是不同机队擦机尾风险进行模拟5 000次后的结果(着陆俯仰角为负值时，风险值记为0)，从图中可以看出，当飞机着陆俯仰角相同时，两机队擦机尾的风险值不同：当着陆俯仰角度数小于4.5°时，两机队的擦机尾风险值无太大区别，但当着陆俯仰角大于4.5°时，机队2擦机尾风险明显大于机队1，如当飞机着陆俯仰角为5°时，机队1擦机尾风险值为1.70，机队2擦机尾风险值为2.03，航空公司可据此加强对机队2飞行员的训练,降低擦机尾的风险。

蒙特卡洛模拟指标汇总如表2所示。通过蒙特卡洛模拟得出预测结果的最大值、最小值和最可能值，给出了擦机尾风险值的预测区间范围及分布规律，证明此模拟方法能较为合理地预测风险。

表2 蒙特卡洛模拟指标汇总Table 2 Indicator summary of Monte Carlo

注：以上数据均是通过MATLAB模拟显示的最终结果，其中着陆俯仰角的模拟次数为5 000次。

4 结论

1)本文利用原始QAR数据作为样本，基于蒙特卡洛方法对飞机着陆时的擦机尾风险值进行预测，进行模拟抽样试验5 000次，较好地解决获取航班信息有限的问题。

2)利用蒙特卡洛算法进行模拟，能够比较准确地估算出整个机队在某一运行周期内起飞或着陆阶段擦机尾的风险值，适用于单个航班擦机尾风险值的预测，也适用于整个机队在一段时期内擦机尾风险预测，还可延伸到其他超限事件的风险评估，为航空公司的超限事件管理提供可靠性指标参考，实现对机队操作风险的动态管理。

3)该风险预测方法虽模拟出飞机着陆时擦机尾的风险值，但是由于飞机在着陆时受到诸多因素影响，各因素对风险产生的影响需进一步研究。