*可折叠微板上的细胞牵张力的计算

王丽丽，陈维毅

(太原理工大学 生物医学工程学院，太原 030024)

细胞牵张力(cell traction forces,CTFs)，即细胞收缩力，通过肌动球蛋白的相互作用和肌动蛋白的聚合作用产生的，方向指向细胞体的中心，在很多生物学过程中发挥重要作用，如细胞铺展炎症、伤口愈合、血管再生和肿瘤转移等[1-2]，如图1所示。CTFs的测量可追溯到20世纪80年代，HARRIS et al[3]将细胞接种在薄硅胶膜上，发现正在迁移的细胞使硅胶膜产生褶皱，通过分析褶皱的数量及长短，发现小GTPase RhoA和钙调蛋白信号途径通过应力纤维和局部FAs参与CTFs的调控[4-5]。然而，薄硅胶膜测量CTFs仅局限于高度收缩性的几种细胞，而且由于薄膜发生非线性褶皱变形，导致力学分析比较困难。有学者改进了上述测量方法，在非起皱硅胶弹性膜上包被微米级乳胶小球，细胞产生牵引力使微球的位置发生变化，但并不引起弹性薄膜起皱[6]。根据小球的位移变化估算牵张力的矢量，但小球的位移和牵张力之间的关系仍为非线性，依旧不能采用弹性理论进行分析。DEMBO et al[7]将细胞培养在软的凝胶或高分子聚合物弹性基底表面，基于小变形假设，采用线弹性连续介质理论进行分析计算CTFs场[8]。此方法的优势在于聚丙烯酰胺凝胶属于线性弹性材料，外力消失后，形变可恢复[9]；不足之处在于所用的弹性基底本身会发生变形及荧光粒子位移的测量使此方法精确度受到一定限制，观测数据的微小偏差可能导致解的离散。

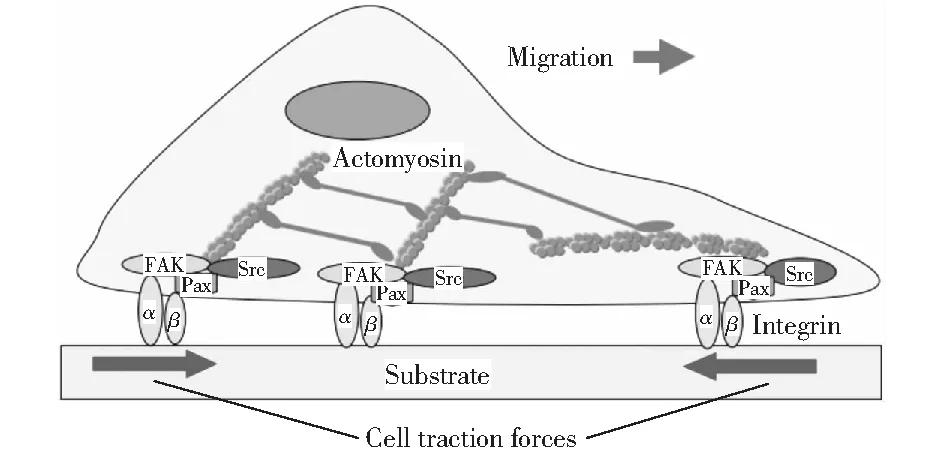
图1 细胞牵张力示意图[2]Fig.1 Schematic diagram of cell traction force[2]

也有学者用水平式的微组装悬臂梁和微柱力传感器阵列技术[10-12]测定细胞牵张力(图2).BENINGO et al[13]采用“夹心”的方法，结合细胞牵张力显微镜技术(traction force microscopy,TFM)检测了细胞在三维微环境中所产生的牵张力。虽然采用上述测量CTFs技术部分实现了细胞在三维微环境中CTFs的估算，但受技术本身的缺陷影响，实现细胞在三维微环境中牵张力的测量需要提高和改进。

图2 微柱上细胞铺展及牵张力产生机制示意图[12]Fig.2 Schematic representation of cell spreading and force generation mechanism on micropillar[12]

在微制造领域，与立体平面印刷术和激光微加工技术相比，折纸折叠技术因其操作简单、省时等优点，已被证实是制造三维微结构非常有前景的方法[14]。最近采用折纸折叠技术制造出了载有细胞的纳米尺度的微结构[15]人工组织支架[16]和手术夹具[17]等，由于这些微结构需要额外的激发因子所产生的表面张力或铰链收缩来实现折叠，而这些驱动力的产生需要功能材料，如n(Cu)∶n(Cr)复合金属或热敏聚合物，若应用到活细胞研究中，则需考虑其生物相容性。2012年日本东京大学研究人员建立了细胞折纸(cell origami)CTFs系统(图3)，利用细胞牵张力将具有生物相容性的聚对二甲苯(Parylene)薄膜折叠[18]，并通过改变薄膜的二维形状及排列，构建了不同的三维空间结构，并通过增加“铰链结构”来精准控制折叠角度。

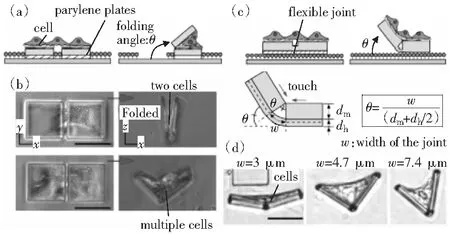
图3 折叠角示意及实验图[18]Fig.3 Schematic illustration of folding angle and experiment[18]

虽然上述材料在实现三维微结构时不需要额外的激发因子，简单高效，且细胞折纸法获得的细胞牵张力的精度约是DEMBO et al[7]方法的3倍，但他们只给出了一种测量CTFs的平台，并没有定量的力学分析依据和更加深入的应用。因此本研究拟通过自折叠2D微板(self-fold flat microplates)建立测量CTFs细胞折纸的理论计算模型，通过改变微板2D形状、尺寸和刚度等物理参数建立细胞折纸系统的折叠角度和弯矩的关系，并通过有限元方法验证公式的合理性。

1 弯矩与折叠角的关系表达式

本文首先将微板看成是只受弯矩影响的纯弯曲梁(图4)[19]，用横截面m-m和n-n从梁中取长度为dw的微段，设梁的轴线为x轴，横截面的对称轴(纵向对称面)为y轴，中性轴(中性层与横截面的交线)为z轴，弯曲后，截面m-m和n-n间的相对转角为dθ，从几何、物理以及静力学方面推导得出弯矩M(θ)和折叠角θ之间的关系表达式：

(1)

式中：M(θ)是CTFs所合成的合力矩；Iz是对转轴z的惯性矩；E是微板的弹性模量；w是微板刻痕的宽度。根据几何关系可知[18]：

(2)

式中：dm是刻痕处微板的厚度；θ是折叠角(图3)；dh是铰链厚度。得出微板弯曲时的弯矩M(θ)与其几何尺寸的关系表达式：

(3)

图4 微板弯曲示意图Fig.4 Schematic illustration of microplates bending

2 细胞牵张力与折叠角的关系表达式

由于细胞牵引力对于许多生物学过程非常关键，决定着许多细胞功能，包括细胞迁移、细胞铺展炎症、信号转导等。准确测量细胞牵引力的大小以及分布对细胞生物学、组织工程等生物医学研究有重要意义[20]，基于生物微机电系统技术制作的微悬臂梁阵列作为细胞牵张力合力公式为：

(4)

式中：R是圆柱体微悬臂梁的半径；h是圆柱体的高；E是微柱的弹性模型；δ是微柱在牵张力作用下产生的挠度；θ是转角。

根据式(3)中折叠角θ和弯矩M(θ)的关系表达式，可得出微板的折叠角θ与单位长度细胞牵张力f的关系式，对细胞内的微丝分布(如图5所示)作如下假设：

1) 假设细胞内微丝均匀分布；

2) 假设细胞内微丝牵张力均匀分布。

图5 细胞内微丝分布示意图Fig.5 Schematic illustration of the microfilament distribution

垂直于斜面的均布载荷的合力Fy大小为：

(5)

弯矩M(θ)的表达式为:

(6)

联立式(1)和式(6)，可得单位长度牵张力f与折叠角θ之间的关系表达式：

(7)

根据表1数据可得，微柱转过角度θ时所需的牵张力合力：

(8)

同理，可得微板折叠角度θ时所需的牵张力合力：

(9)

通过对上式(8)和式(9)进行对比，发现细胞牵张力与θ成正比，这也直接证明了式(7)的合理性。因为采用微柱力传感器阵列技术测定CTFs时受技术本身缺陷的影响，所以实现细胞在三维微环境中牵引力的测量需要提高和改进，而利用微板折叠计算细胞牵张力时，只需通过改变微板的二维形状及排列就可构建了不同的三维空间结构，真正实现了在三维环境中测量细胞牵张力。

表1 材料参数表Table 1 Properties of the materials

3 有限元模拟

为了进一步验证式(1)和式(7)的合理性，本文采用有限元软件ABAQUS进行模拟，鉴于在计算折叠角θ时，微板的一端不动，另一端折叠，建立的有限元模型如图6所示，所用的材料参数见表1.

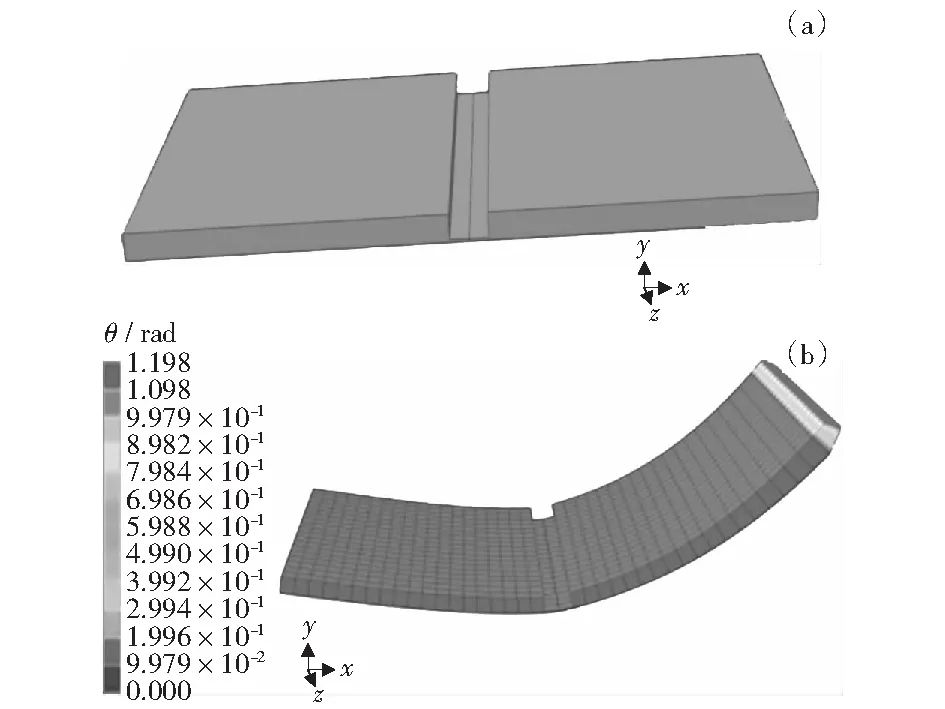
图6 有限元模拟图Fig.6 Schematic diagram of finite element simulation

应用式(2)及表1的数据可得微板模型的最大折叠角为：

(10)

根据式(1)可得：

(11)

有限元计算时通过给定不同的弯矩值，可得到相应的转角，见表2.

表2 弯矩M(θ)与转角θ的模拟值Table 2 Simulation values of moment and angle

通过拟合有限元计算的结果，得到刚度k的值，如图7所示。

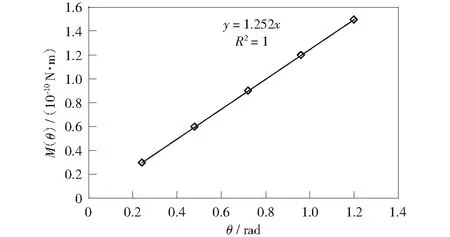
图7 刚度k值Fig.7 Value of stiffness k

有限元拟合得到的刚度k值与理论计算结果进行比较，其误差值e如式(12)所示。

(12)

4 结果与讨论

根据材料力学纯弯曲理论计算了微板折叠时折叠角和弯矩之间的关系，首先通过有限元验证了弯矩与折叠角的关系式的合理性；其次，通过与微柱力传感器阵列技术测定细胞牵张力，对比验证了细胞牵张力与折叠角关系表达式的正确性。通过上述简要分析，可得在利用细胞收缩折叠微板时，可以将其看成一个纯弯曲的折叠问题，弯矩与折叠角成正比关系。同时也为下一步通过微板折叠角来计算细胞变形后的形状以及细胞产生的牵张力的大小和方向提供了一定的理论依据。

本文的主要工作侧重于理论研究，在利用细胞的收缩力折叠微板时，并没有考察细胞的形状及细胞产生的力的大小和方向，只是简单地假设细胞产生的合力合成的弯矩来计算折叠角，有限元计算结果与理论计算结果对比，尽管误差略大，但也可简要的表明计算模型的合理性。