基于边际效用模型的最佳人力资源管理模型

2019-03-05孙文亮

统计与决策 2019年2期

孙文亮

（南开大学经济学院，天津 300071）

0 引言

人力资源在企业资源中占据重要地位，企业只有具备完善的激励体制，才能储备更多各行业的优秀人才，进而最大程度地提高员工的积极主动性和创造力，提高企业的经济效益。目前我国各大小企业中均有相应的激励机制，但效果并不明显，这主要是因为缺乏对效用理论的应用。公司的激励制度按照效用理论可分为物质激励（边际效用递减规律）与精神激励（边际效用递增规律）两种。在一定时间内，边际激励效用会随着激励数量的增加而呈递减趋势，在原有条件不变的情况下，员工接受到的总效用会随着激励的增加而增加，但是效用却会减少。同时，企业在运用边际效用模型时，投资成本会一直增加，最终所得报酬增加也会在达到极限后降低。本文运用边际效用模型构建企业人力资源的优化模型，利用企业经济增长模型计算出边际效用的变化，分析人力资源管理对企业生产总值的影响，并对其进行优化配置。

1 边际效用模型的构建

1.1 边际效用函数

假设m是人力资源管理质量的指标个数，yj则为第j个指标的资源投入总量，是指标效用。而在市场环境中，人力资源是作为特殊商品存在的，且同样适用于边际效用规律——yj与满足这个规律，即：

显而易见，与yj之间为上凸曲线，其原点为左端点。将指数分布的概率密度函数作为指标的边际效用函数，将分布函数作为效用函数，即为：

由于/dyj=βj（yj=0），所以，第j个指标所能做到的最大边际效用为βj。

1.2 基于边际效用的人力资源管理模型

设人力资源管理总效用为S，资源投入总量为yj，因此：

式（3）中，ωj代表各指标重要性的权重系数，指第j项指标的效用，yj指资源投入总量。接下来构建两种优化模型。

模型Ⅰ：

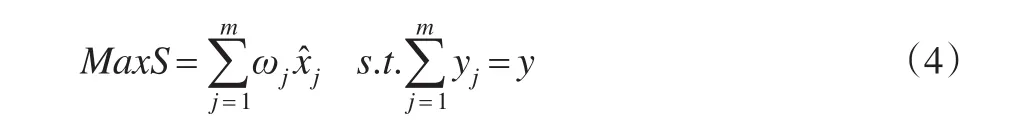
模型Ⅱ：

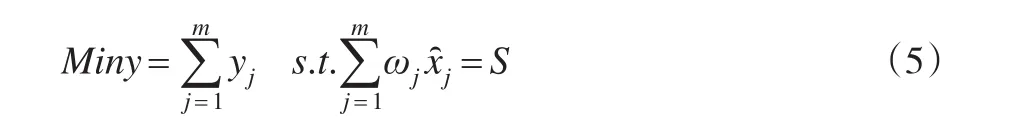
模型Ⅰ的前提条件是在资源投入总量有限的情况下，使其总效用运用最大化的最优化模型；模型Ⅱ是以目标明确为基础，使投入量最小的最优化模型。

假设在研究过程中，已经精准评估了与yj，可将式（2）变为：

式（6）便是βj的求解式。

1.3 模型求解

（1）模型Ⅰ：

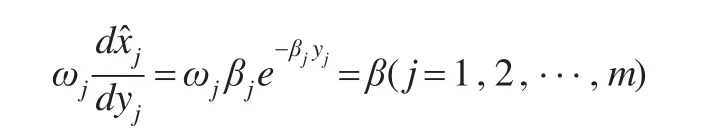
即为：

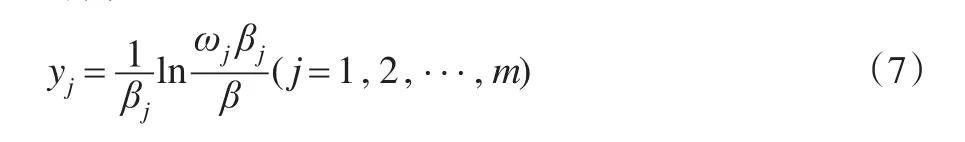
而事实证明，当yj＞0时，ωjβj＞β，因此只要对其范围内的指标进行投资，设满足该条件的指标为前J个指标，则有：

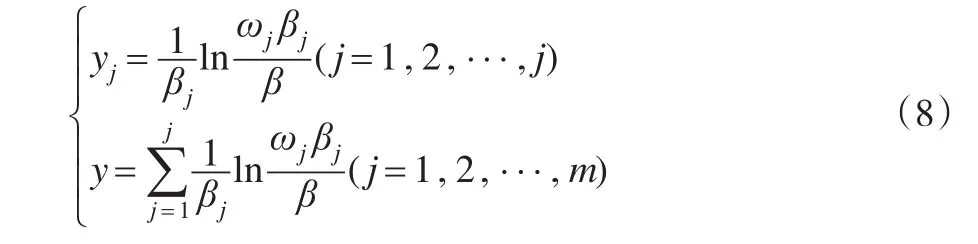
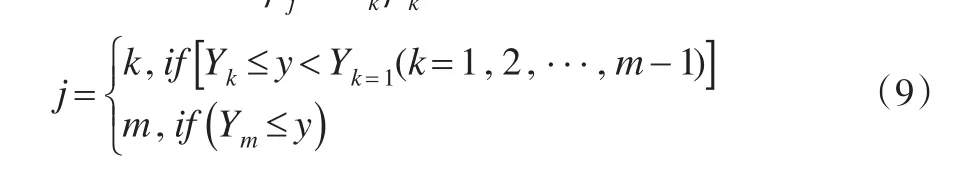
将式（9）中所得的 J值代入式（8），并记ϖj=可得：

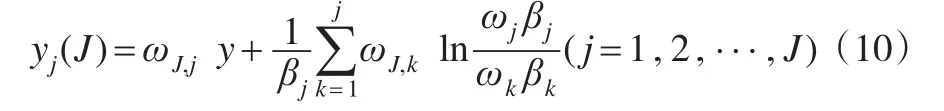
因此，式（10）为模型Ⅰ的最优解。

（2）模型Ⅱ

依据模型Ⅰ：

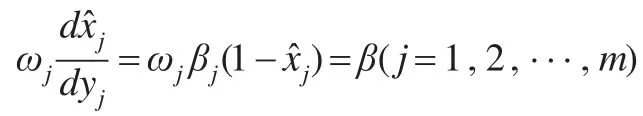
则有：

当＞0时，有ωjβj＞β，因此只要对其范围内的指标进行投资，设满足该条件的指标为前J个指标，则有：

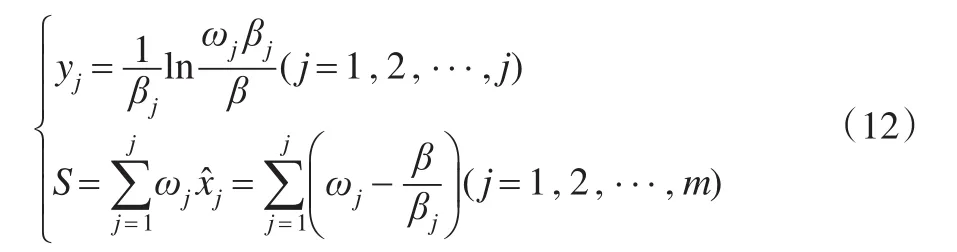
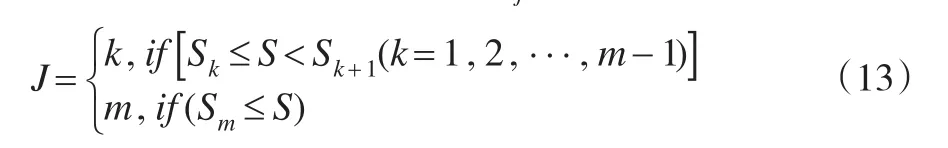
将式（13）的J值代入式（12），可得：

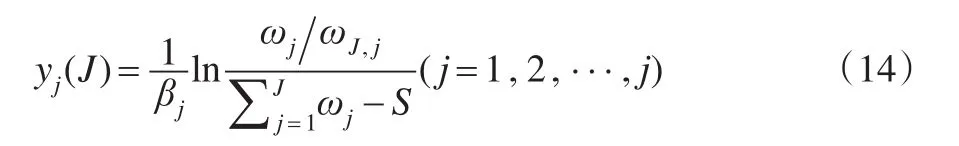
式（14）则为模型Ⅱ的最优解。

1.4 参数求解

现详细说明并解答上述模型中所含有的参数。

（1）ωJ，j

同时求解式（10）：

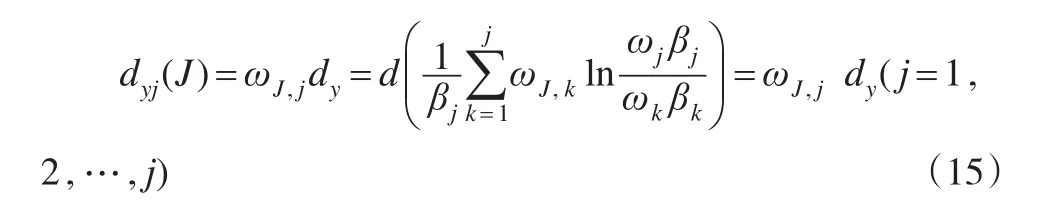
式（15）说明，在模型Ⅰ的最优解中，y每增加dy，各指标相应增加资源同理，求解式（14）：

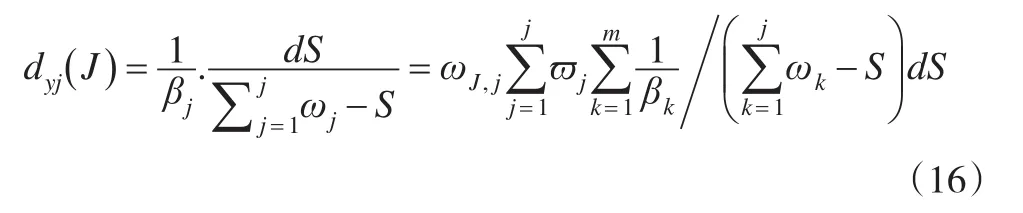
（2）ϖj

由ωJ，j和ϖj可知，当J=m时，ωm，j=ϖj，并可将ϖj作为指标的特征权重，因此，由式（14）及式（18），查看y→∞和S→1-的极限情况为：

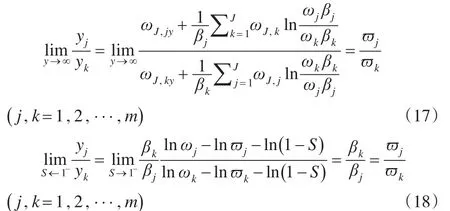
由式（17）和式（18）可知，ϖj是在y→∞或S→1-的情况下，满足模型Ⅰ和模型Ⅱ的指标投资权重，ϖj即是各指标最佳投资权重所得的收敛值。

2 实证分析

某企业对其专业技术人才管理情况进行绩效考核预评价，职位分析与评价、素质模型、人才规划、职务评任、培养提高等8个一级指标共同组成了评价指标集Cj，其中j的取值为1，2，…，8，ωj、、yj分别代表指标权重、在j指标上产生的效用、各指标资源投入成本（单位：万元）。表1为某企业人力资源管理质量数据。

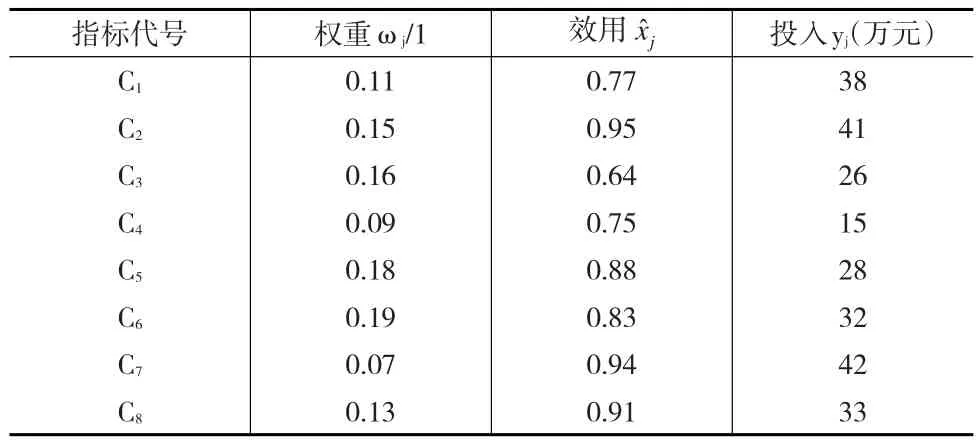
表1 某企业人力资源管理质量评价数据

2.1 基于模型Ⅰ的优化方案

采用模型Ⅰ的优化方案，此方案为管理总效用在固定的272万元总资源投入下达到最大值。由上述推导结果可以从以下三个步骤求解模型Ⅰ的最优解。

第一步：对最大边际效用进行计算，根据式（6）对βj进行计算，并按照从大到小的顺序对最大边际效用进行排序；

第二步：对投资范围J的最佳解进行计算。根据式（9）就能将最佳投资范围计算出来，y＞Y8=103.6，J=12；

第三步：对投资额度的最优值进行求解。当投资范围为10时，式（10）则为：

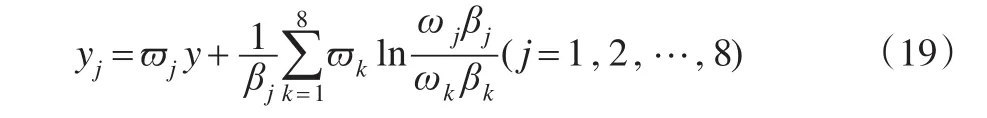
在式（19）中将最大边际效用值与收敛值ϖj代入，各指标最佳投资额度yj就能计算出来[1]。

模型Ⅰ的优化方案求解结果如表2所示。

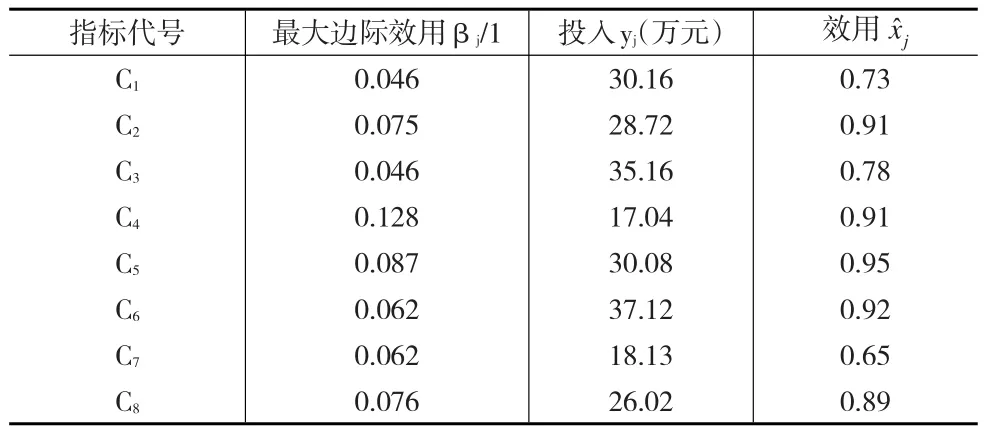
表2 模型Ⅰ的优化方案求解结果

优化方案中，当投入资源计划总量保持在272万元的情况下，人力资源管理总效用预期值为0.823，比原方案的总效用提升了4.04%。

2.2 基于模型Ⅱ的优化方案

采用模型Ⅰ的优化方案，此方案为资源投入总量在固定的0.791人力资源管理总效用下达到最小。由上述推导结果可以从以下三个步骤求解模型Ⅰ的最优解。

第一步：对最大边际效用进行计算，根据式（6）对βj进行计算，并按照从大到小的顺序对最大边际效用进行排序；

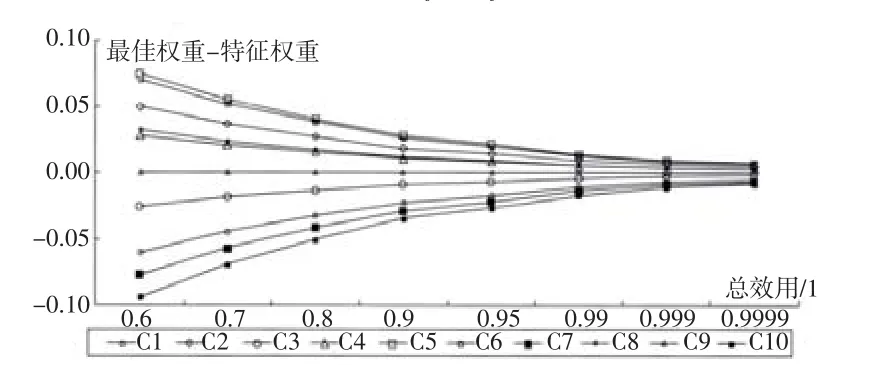
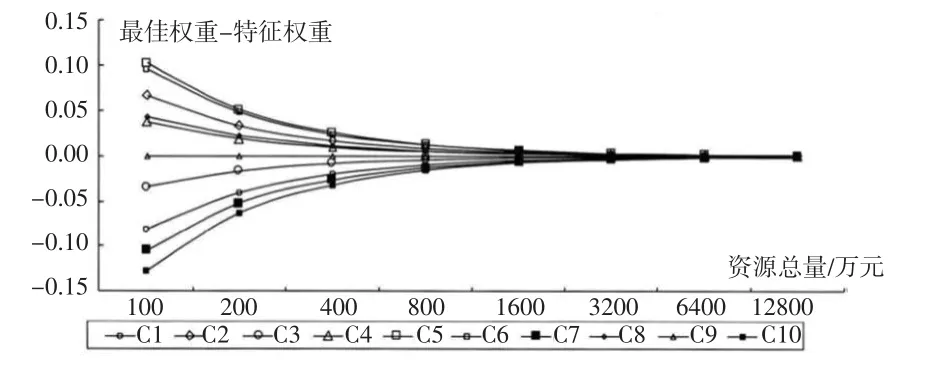
第二步：对投资范围J的最佳解进行计算。根据式（13）就能将最佳投资范围计算出来，S8=0.522

第三步：对投资额度的最优值进行求解。当投资范围为10时，式（14）则为：

在式（20）中将最大边际效用值与收敛值ϖj代入，各指标最佳投资额度yj就能计算出来[2]。

模型Ⅱ的优化方案求解结果如表3所示。

优化方案中，当人力资源管理总效用预期为0.791的情况下，计划人力资源总量的计划投入仅为251.3万元，比原方案的资源投入降低了8.24%。

2.3 指标最佳投资权重与特征权重

为进一步对指标最佳投资权重与特征权重之间的关系进行分析，本文利用上述算例数据，分析了指标最佳权重随其他两个指标的变化趋势，具体结果如图1与图2所示。图中指标最佳投资权重为[3]：

表3 模型Ⅱ的优化方案求解结果

图1 指标最佳投资权重随总效用变化趋势

图2 指标最佳投资权重随资源投入总量变化趋势

由图1和图2可知，模型Ⅰ与模型Ⅱ最佳解的指标权重与相应的特征权重之差随着不断增加的总效用与投入总量而逐渐收敛于“0”。因此，各指标最佳投资权重的最终收敛值为指标特征权重。此现象代表：虽然指标最大边际效用、指标权重与总效用共同影响最佳指标投资权重，但是最佳指标投资权重随着资源总投入或总效用的增加而受到指标权重与总效用的影响逐渐减小，对其影响逐渐增加为最大边际效用，并最终向指标特征权重收敛。