跳跃-扩散模型基于拉普拉斯变换的参数估计

韩 潇

（山东农业工程学院 会计学院，济南 250100）

0 引言

近几十年来，随着金融产品的多样化，尤其是金融衍生产品的不断涌现，金融随机模型的构建打破了传统假设，日益完善，与此同时模型的数学形式也更加复杂化。因此，对于模型参数的估计已不能满足一些经典估计方法的假设或由于模型过于复杂而没有确切的解析式等，从而使经典估计方法失效。为此，通过研究基于拉普拉斯变换的估计，获得有效的拉普拉斯变换估计量，将其应用于金融随机模型跳跃-扩散模型中，为解决实际金融产品及其衍生产品的定价等问题的研究提供恰当的参数估计方法。

1 跳跃-扩散模型

通过对几何布朗运动过程添加跳跃过程，莫顿提出了混合布朗-泊松过程[1]：

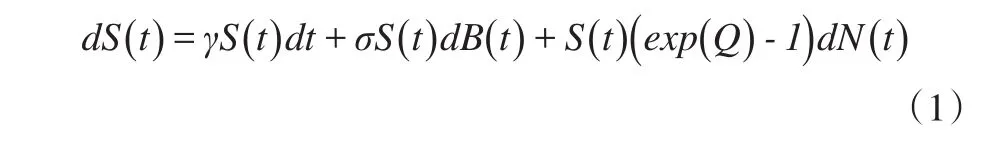
其中，B(t)为标准布朗运动，N(t)为强度参数为λ的泊松过程，B(t)和N(t)两者相互独立，γ为瞬时漂移，σ为瞬时波动率。

2 基于拉普拉斯变换的估计量及其渐进分布

为了更方便地处理统计模型，令b为实数域中的拉普拉斯变换参数，这时的拉普拉斯变换为:

设x1,x2,…,xn为随机变量X的n个观察值，则经验拉普拉斯变换为：

2.1 独立同分布的情况

设θ为参数向量，θ=(θ1,θ2,…,θp)T（其中，P＞1,T为转置），则随机变量X的拉普拉斯变换为其变换参数向量为以及其观测值的经验拉普拉斯变换为

其中，fb是gb的反函数。

(b)的渐近分布表示为：

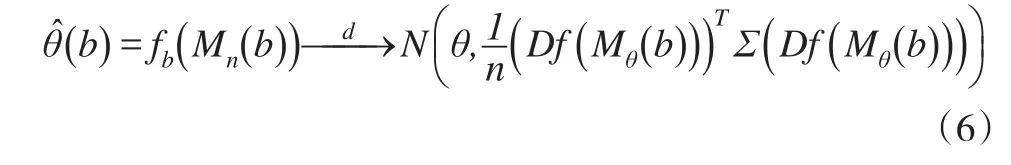
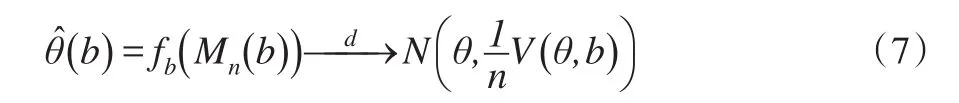
2.2 非独立同分布的平稳过程

用经验拉普拉斯变换估计严格平稳的随机过程并不完全类似独立同分布的情形，由于需要考虑到相关性，类似于边际经验累积分布函数，边际经验矩母函数在相关的数据的情况下可能无法定义所有的参数或者会导致效率的损失。因此，需要通过一些特殊手段来实现近似。

定义随机过程数据X1,X2,…,XT的数据移动块为因此，每个数据块包含m+1个观测值，并且与其相邻块有m个重叠的时期。各块的联合拉普拉斯变换被定义为：

其中，b=(b1,b2,…,bm+1)T为m+1维变换向量变量。联合经验拉普拉斯变换定义为：

其中，n=T-m

其中，fb是函数gb的反函数。

当随机过程为时齐独立增量过程时，具有马尔科夫性质，则其不重叠区间上的增量相互独立。若X(ti)为时齐独立增量过程，则互不重叠的区间上的状态增量相互独立，并且其分布函数只依赖于时差Δt。

给出一组时间ti,i=0,1,…,n，满足Δt=ti-ti-1，则为独立同分布的随机变量，则可以根据独立同分布的情况进行估计。

2.3 最小方差估计量

为了寻找基于拉普拉斯变换估计的最有效的估计，拉普拉斯变换参数的最佳选择是令V(θ,b)最小化，定义为：

b*(θ)是令达到最小的最佳b值。如果b*(θ)独立于θ,记为b*,可以直接获得估计量：

更多情况下，b*(θ)依赖于θ。在这种情况下，提出了自适应估计量和经验最小方差估计量来克服这一问题。

2.3.1 自适应估计量

首先，在参数空间中任意选择b1，并通过式（5）获得估计量然后将中的θ更换为并最小化将得到的新值标记为b2。接着得到然后计算b3，以此类推。重复迭代，最终获得无限序列如 果 迭 代 收 敛 ，即当k→∞，则并且θ可以通过估计量进行估计定义为自适应估计量[2]。

其中，u是关于θ和b的方程，令u=h(b,θ)，则：

记u*为令v(u)最小的取值。因此，通过式（13）令获得bA，然后从式（15）获得

2.3.2 经验最小方差估计量

用来估计θ的经验最小方差估计中的bE是使最小化的b值，即在b=bE时，取最小值[3]。因此，通过式（5），经验最小方差估计是：

通过证明，自适应估计经常被定义为经验最小方差估计，他们的渐进性质是相同的[2]。

3 基于拉普拉斯变换的估计在跳跃-扩散模型中的应用

3.1 基于拉普拉斯变换的估计

则其理论拉普拉斯变换为：

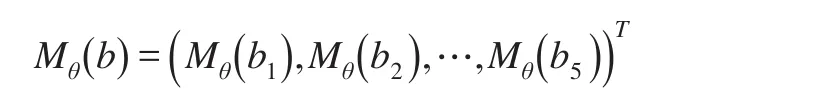
其中，θ=(μ,σ,λ,ν,δ)T,b=(b1,b2,b3,b4,b5)T,Mθ(bi)参见式（18）。

经验拉普拉斯变换为：

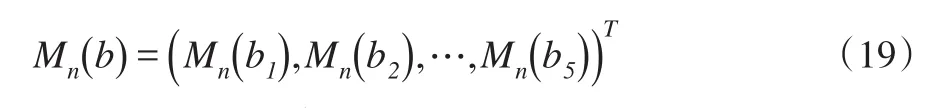
θ的估计量是通过方程组2,…,5，求解θ所获得的。

关于b=(b1,b2,b3,b4,b5)T的选取是令达到最小值。

3.2 模型的蒙特卡罗模拟

通过计算机（Matlab软件）模拟数据过程:

首先模拟复合泊松过程，产生随机指数分布变量T~expontial(λ),令

3.3 模型估计

基于拉普拉斯变换估计计算机（Matlab软件）求解过程：

第一步：给出初始b值，计算估计量

第三步：用求解出的值替换初始b值，重复上述步骤。直至

在实际求解多参数过程中，由于拉普拉斯变换估计变换方式相同，唯独变换参数取值不同，最小方差估计的判定矩阵选出的b的取值相近，而使参数估计矩阵接近奇异，难以准确估计。

为解决该问题，根据当随机过程为时齐独立增量过程时，具有马尔科夫性质，则其不重叠区间上的增量相互独立。若X(ti)为时齐独立增量过程，则互不重叠的区间上的状态增量相互独立，并且其分布函数只依赖于时差Δt。因此，略微调整数据的变换，计算5列数列Y1,Y2,Y3,Y4,Y5分别为时差1Δt,2Δt,3Δt,4Δt,5Δt的不重叠的区间上的状态增量数列。

则其经验拉普拉斯变换为：

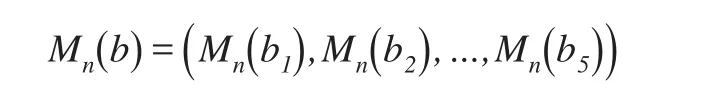
3.4 蒙特卡罗模拟实验

选择样本量n=1000，分别选择参数θ=(0,1,10,0,0.5)T；

θ=(0,1,15,0,0.5)T进行数据模拟。对每种情况重复实验2000次，其估计效果数值参见表1。

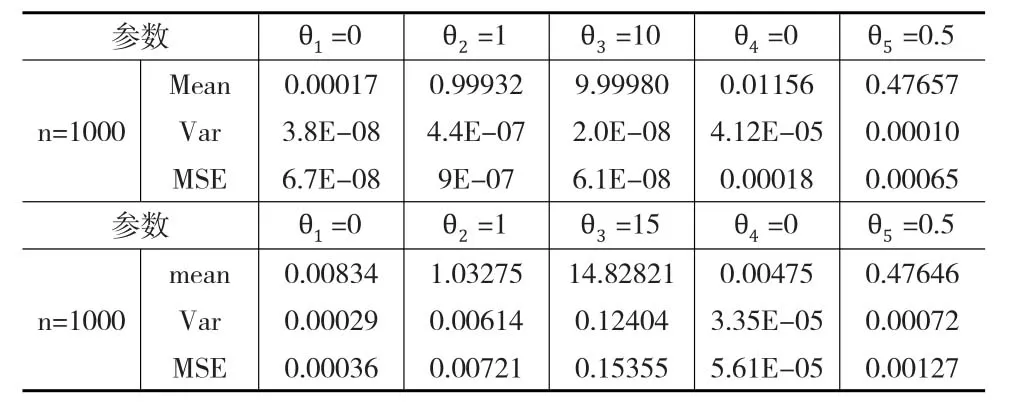
表1 参数估计值的蒙特卡罗模拟结果

从实验结果可以看出，通过改进基于拉普拉斯变换的估计可以较好地估计跳跃扩散模型的参数。

4 结论和讨论

通过研究基于拉普拉斯变换的估计，获得有效的拉普拉斯变换估计量，将其应用于金融随机模型跳跃-扩散模型中，通过模拟分析，可以得到预期的估计效果。为解决实际金融产品及其衍生产品的定价等问题的研究提供参数估计方法参考。

基于拉普拉斯变换的估计量在某些情况下具有一些理想的性质，例如，当样本量非常大时，有一致性和渐近正态性[4]。而当最大似然估计不可用的情况下，基于拉普拉斯变换的估计可获得较为有效的估计结果。但值得注意的是基于拉普拉斯变换的估计并不总是可用的。此外，如果选择变换参数b的判断式的最小化依赖估计参数θ，则会导致效率的损失。并且在一些情况下所述变换参数b的增加并不总是提高估计的性能。在一些情况下，只用较少的变换参数得到最佳的效率，例如判断式是凸函数，只有一点是合理有效的，由于这个原因，有时使用单点的情况是优于使用多点的情况。

在对跳跃扩散模型进行估计时，可以得到预期的估计效果。但由于参数较多，其拉普拉斯变换方程组为非线性方程组，没有闭合的解析式，计算复杂。同时，渐近分布是没有具体表达式的形式，需要在平衡效率和复杂性上做出选择。在利用Matlab软件求解时，变换参数的选择矩阵由于含参数较多以及形式复杂，并且在某些取值下接近奇异阵而产生一系列影响数值求解精度的问题。而且在求解选择矩阵的最小值时，由于软件解析所限，须验证是否是全局最小值，而非局部最小值，因此，需要验证解的真实性。由于以上种种原因导致求解过程耗时较长。