只有输出的广义样本区间DEA模型
2019-03-05马占新
伊 茹,马占新
(1.华北电力大学经济与管理学院,北京 102206;2.内蒙古大学经济管理学院,内蒙古 呼和浩特 010021)
1 引言
数据包络分析[1-2](DEA)是使用数学规划模型评价具有多输入、多输出决策单元间的相对有效性。自1978年由Charnes等人提出以来,众多学者在模型的扩充和完善相关理论的发展以及DEA应用方面都进行了大量研究[3-7]。近期学者们在传统DEA方法的基础上,从非期望产出[8-10]、交叉效率中决策单元的排序[11-12]、输入输出变量约束[13-14]等角度展开了进一步的研究。针对传统DEA方法只能给出决策单元相对于有效决策单元的评价信息,无法依据指定参考集提供评价信息的弱点,马占新[15-16]从评价参考集的角度出发,对数据包络分析理论进行拓展,提出广义DEA方法,之后,对广义DEA模型进行扩充与完善,分别提出带有偏好锥的广义DEA模型[17]、包含无穷多个样本单元的广义DEA模型[18]、综合的广义DEA模型[19],并对决策单元偏序关系[20]进行了系统的研究。针对广义DEA模型中样本单元和决策单元的投入、产出数据非准确数的情况,孙娜等[21-22]分别提出了广义超效率区间DEA模型和广义模糊DEA模型,并对其有效性进行了研究。传统DEA方法和广义DEA方法作为非常有效的效率评价方法难于评价非效率问题。为此,马占新和伊茹[23]给出基于样本评价的非参数综合评价方法,将传统DEA方法的功能由“效率评价”推广到了包含“非效率评价”在内的更一般的情况,并对非效率型DEA参照系进行了拓展性研究,但该方法只是针对指标值为精确数的情况。
在综合评价过程中,根据不同目的人们选择不同的参照标准对评价对象鉴定优劣、区分等级、排列次序。由于评价目的的不同和客观事物的复杂性,参照对象和评价对象指标数据采用区间数,具体表现形式为:(1) 由于个体存在差异,有些指标数据可在一定范围内波动,故人们选用参考值范围作为标准,判定评价对象是否处于参考标准范围内;(2)由于客观事物的不确定性,评价对象指标观测值选取为可能的取值范围,此时人们选择可接受的特定标准考察评价对象指标取值范围是否达到了预期标准;(3)当评价指标存在定性指标时,可采用区间数形式对其进行量化,此时面临参照对象和评价对象指标值均为区间数的情况。针对上述问题,无法简单地应用传统DEA方法及其改进方法去综合评价决策单元的有效性,必须考虑新的处理方法对各决策单元进行综合评价。
针对已有文献研究中存在的不足和上述现实中存在的问题,本文通过分解的方法讨论样本单元和决策单元指标信息为区间数时用广义DEA模型评价决策单元有效性的方法,并相应地构建了只有输出的广义区间DEA模型。同时,对模型的含义、求解以及性质等进行了分析。之后,探讨了该方法在决策单元有效性分类和排序中的应用。最后,通过实例表明该方法的可行性和有效性。
2 只有样本单元的输出为区间数
2.1 区间样本可能集的构造及IS-E有效性


为了给出区间样本参考集下的决策单元有效(简称IS-E有效)概念,以下分三种情况进行讨论:
(1)当评价指标为效益型,则区间样本可能集TIB表示为:
TIB={Y|Y其中,由区间数的运算法则[25]可知,仍为区间向量。比较区间≥当且仅当且≥1和≥2表示两个基本的序关系,⟺≥⟺≥下文中的区间比较同理。
定义1如果不存在Y∈TIB,y∈Y,使得yyp且至少有一个不等式严格成立,则称决策单元p为IS-BE有效。
(2)当评价指标为成本型,则区间样本可能集TIC表示为:
TIC={Y|Y
定义2如果不存在Y∈TIC,y∈Y,使得yyp且至少有一个不等式严格成立,则称决策单元p为IS-CE有效。
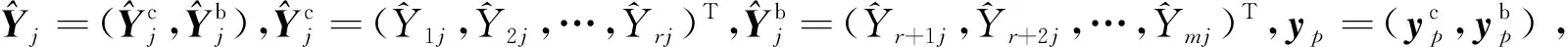
TIBC={Y|Yc
定义3如果不存在Y∈TIBC,y∈Y,使得(yc,-yb)且至少有一个不等式严格成立,则称决策单元p为IS-BCE有效。
2.2 基于区间样本可能集的决策单元有效性度量模型及有效性判定
根据上述区间样本可能集,可以建立度量决策单元IS-E有效性的只有输出的广义区间DEA模型:
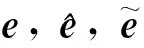
为了应用上述模型判断决策单元IS-E有效性,以下给出进一步的分析:


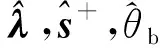
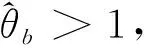
(⟸)若决策单元p为IS-BE无效,则由定义1可知存在Y∈TIB,y∈Y,使得yyp且至少有一个不等式严格成立。因此存在λ0使得故可知的最优值大于1,矛盾。证毕
类似可证以下定理2和定理3成立。
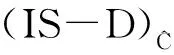
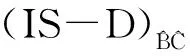
上述三种模型均是非线性规划模型,可通过两组线性规划模型对其进行求解。
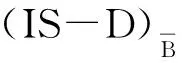
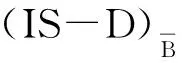
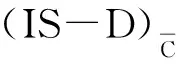
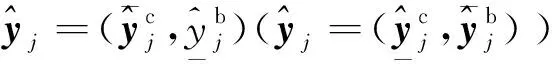

2.3 决策单元的IS-E有效性分析

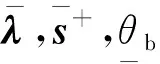
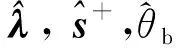
类似可证以下定理5和定理6成立。
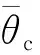
2.4 基于IS-E有效性的决策单元分类及排序
根据决策单元区间有效值,可将所有决策单元p(p=1, 2,…,n) 分为以下几类:



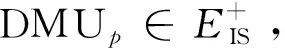
通过上述分析,基于区间样本可能集的广义DEA区间有效值反映了决策单元的有效性程度,因此,可根据区间有效值对决策单元进行排序。
为了便于说明决策单元基于区间样本单元的IS-E有效性评价问题,通过评价效益型输出指标的决策单元为例具体说明:
例1考虑具有两种效益型输出指标的2个区间样本单元和3个决策单元,其相应指标数据见表1。

表1 区间样本单元和决策单元输出指标数据
应用模型(IS-D)B可得表2中的结果,相应的区间样本可能集和决策单元的分布可由图1表示出来。

表2 决策单元IS-E有效值

图1 效益型输出的广义区间DEA样本可能集
由表2中决策单元的有效值可知,决策单元D1、D2、D3分别为强IS-BE有效、弱IS-BE有效和IS-BE无效。图1显示,由于决策单元D1位于最大值样本前沿面所围区域之外,因此强IS-BE有效;决策单元D2位于最小值样本前沿面和最大值样本前沿面所围区域中,则弱IS-BE有效;决策单元D3位于最小值样本前沿面所围区域之内,则IS-BE无效。
3 只有决策单元的输出为区间数
3.1 样本可能集的构造及S-IE有效性

基于样本可能集T的S-IE有效概念以下分3种情况定义:
(1)当评价指标为效益型,则样本可能集TB表示为:
TB={y|y
定义5如果不存在y∈TB,使得yp∈Yp,yyp且至少有一个不等式严格成立,则称决策单元p为S-IBE有效。
(2)当评价指标为成本型,则样本可能集TC表示为:
TC={y|y
定义6如果不存在y∈TC,使得yp∈Yp,yyp且至少有一个不等式严格成立,则称决策单元p为S-ICE有效。
TBC={y|yc
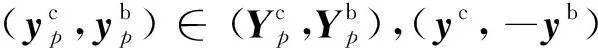
3.2 基于样本可能集的决策单元有效性度量模型及区间有效性判定
根据上述样本可能集,通过引入非阿基米德无穷小的概念,建立度量决策单元S-IE有效性的只有输出的广义区间DEA模型:
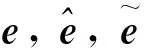
为了应用上述基于样本可能集的只有输出的广义区间DEA模型判断决策单元S-IE有效性,以下进行进一步的分析:
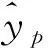
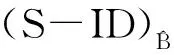
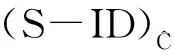
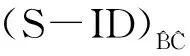
对于上述非线性规划模型,可通过求解决策单元最大值观测点和最小值观测点的有效度量模型,得到区间决策单元p的有效值上限和下限。
当评价指标为成本型,具体度量模型为:
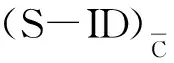
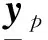



3.3 区间决策单元的S-IE有效性分析
类似可得以下结论成立。
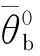
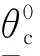
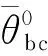
3.4 基于S-IE有效性的决策单元分类及排序
根据决策单元的区间有效值,可将所有决策单元p(p=1, 2,…,n)进行分类:



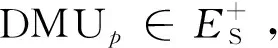
通过上述分析,基于样本可能集的广义DEA区间有效值反映了区间决策单元的有效性程度,因此,可根据区间有效值对决策单元进行排序。
通过评价成本型输出指标的区间决策单元为例,说明区间决策单元S-IE有效性评价问题。
例2 考虑具有两种成本型输出指标的2个样本单元和3个区间决策单元,其相应指标数据见表3。

表3 样本单元和区间决策单元输出指标数据
应用模型(S-ID)C可得表4中的结果,相应的样本可能集和区间决策单元的分布见图2所示。
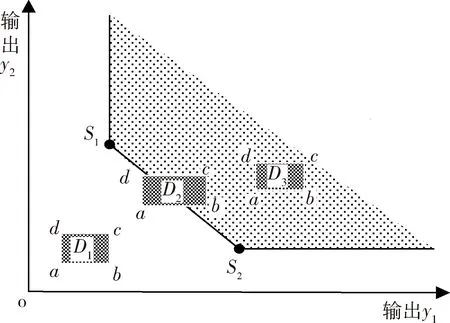
图2 成本型输出的广义区间DEA样本可能集
表4 区间决策单元S-IE有效值

变量单元D1单元D2单元D3θ0cθ-0cθ0cθ-0cθ0cθ-0c有效值1.7163.8330.8161.1860.6020.747
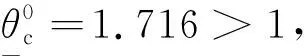
4 样本单元和决策单元的输出均为区间数
4.1 IS-IE有效性
基于区间样本可能集TI的IS-IE有效概念分3种情况定义:
(1)当评价指标为效益型,则基于区间样本可能集TIB,IS-IE有效性可定义为:
定义9如果不存在Y∈TIB,使得YYp且至少有一个不等式严格成立,则称决策单元p为IS-IBE有效。
(2)当评价指标为成本型,则基于区间样本可能集TIC,IS-IE有效性可定义为:
定义10如果不存在Y∈TIC,使得YYp且至少有一个不等式严格成立,则称决策单元p为IS-ICE有效。
(3) 当评价指标为混合型,则基于区间样本可能集TIBC,IS-IE有效性可定义为:
定义11如果不存在Y∈TIBC,使得(Yc,-Yb)且至少有一个不等式严格成立,则称决策单元p为IS-IBCE有效。
4.2 基于区间样本可能集的区间决策单元有效性度量模型
当样本单元和决策单元输出数据均为区间数时,根据区间样本可能集TI,通过引入非阿基米德无穷小的概念,建立度量决策单元IS-IE有效性的只有输出的广义区间DEA模型:
为了求解上述3种非线性规划模型(IS-ID),考虑对区间决策单元最有利与最不利的情形,可得求解决策单元区间有效值上限模型和下限模型,具体如下:
(1) 当评价指标为效益型,则决策单元的区间有效值上限与下限模型如下:
(2)当评价指标为成本型,则决策单元的区间有效值上限与下限模型如下:
(3) 当评价指标为混合型,则决策单元的区间有效值上限与下限模型如下:



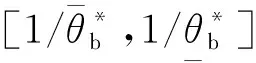
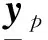
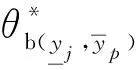
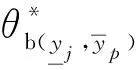
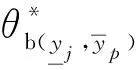
4.3 决策单元有效性分类及排序
依据上述分析,可将所有决策单元p(p=1, 2,…,n)分为以下几类:



定义12若DMUp∈E+,则称决策单元p为绝对IS-IE有效;若DMUp∈E,则称决策单元p为部分IS-IE有效;若DMUp∈E-,则称决策单元p为绝对IS-IE无效。
通过上述分析,广义DEA区间有效值反映了区间决策单元的有效性程度,因此,可根据区间有效值对决策单元进行排序。
5 实例分析
针对样本单元和决策单元指标取值为区间数时的评价问题,现以某地区的商业银行分行运行业绩综合评价为例。为了借鉴其他分行的经验更好地提升企业能力,从而提高企业的竞争力,设20家待评价的分行与同行业内的3家运行业绩突出的同类分行作为标杆进行比较,每家银行采用存款总额,其他存款、发放的贷款、收到的利息、服务费等5个输出指标作为评价指标。表5为标杆分行的输出指标数据,待评价分行输出指标数据参见文献[32]。
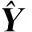
表5 标杆分行的输出指标数据
由于评价指标均为效益型,且标杆分行和待评价分行的评价指标值均为区间数,通过只有输出的广义区间DEA模型(IS-ID)B,求解区间有效值上

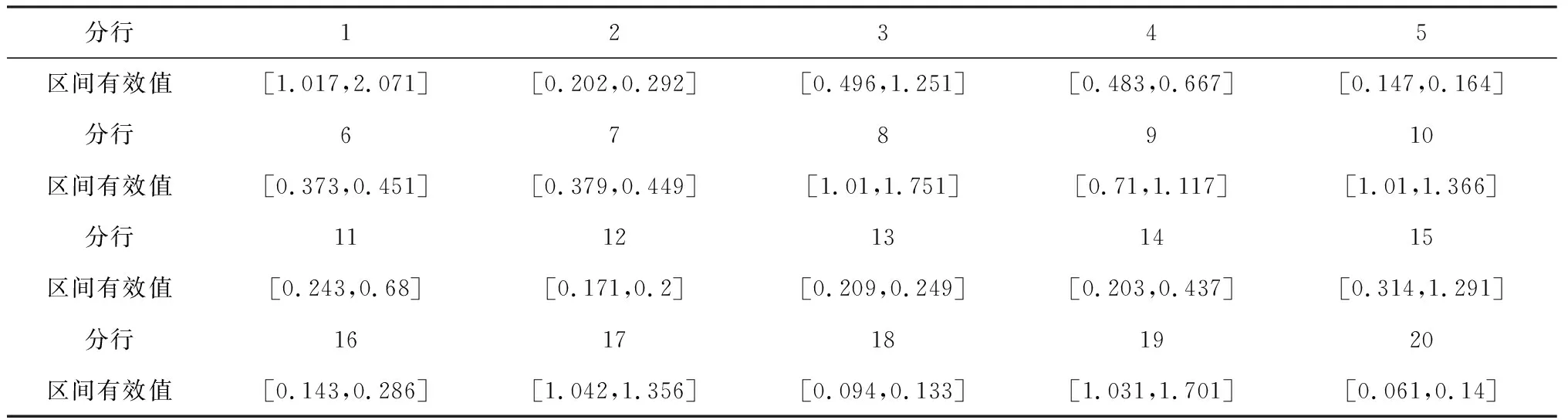
表6 20家分行的区间有效值
对于20家分行的运营业绩综合评价,结合表6中分行的区间有效值,可得以下结论:
(1)分行1、8、10、17、19等5家分行的区间有效值下限值均大于1,即这5家分行均绝对IS-IE有效。表明与选取的3家标杆分行相比,这些分行在各项业绩指标值最低(取区间值的最小值)时的综合运营业绩都高于3家标杆分行在各项业绩指标值最高(取区间值的最大值)时的综合运营业绩。
(2)分行3、9、15等3家分行的区间有效值上限值大于1,下限值小于1,即这3家分行为部分IS-IE有效。表明与选取的3家标杆分行相比,当这些分行在各项业绩指标值最高(取区间值的最大值)时的综合运营业绩高于3家标杆分行在各项业绩指标值最低(取区间值的最小值)时的综合运营业绩,但是当这些分行在各项业绩指标值最低(取区间值的最小值)时的综合运营业绩低于3家标杆分行在各项业绩指标值最高(取区间值的最大值)时的综合运营业绩,说明分行3、9、15等3家分行业绩指标仍有调整的空间。
(3)由于其他剩余分行的区间有效值上限小于1,即其他分行均为绝对IS-IE无效。表明与标杆分行相比,即使这些分行在各项业绩指标值最高(取区间值的最大值)时的综合运营业绩也均低于标杆分行在各项业绩指标值最低(取区间值的最小值)时的综合运营业绩,说明其他剩余的分行综合业绩评价未能达到标杆分行的标准。
根据4.3节决策单元有效性分类,结合待评价分行的运营业绩综合评价情况,可对20家分行运营情况进行如下等级分类,见表7:

表7 分行运营情况等级分类
与此同时,根据表6中待评价分行的区间有效值,可进一步对分行进行运营业绩综合排序。由于20家分行的运营业绩综合评价的有效值为区间数,本文运用模糊左关系方法[33-34]对这些分行进行运营业绩综合排序,可得排序如下:1>8>19>17>10>9>3>15>4>11>7>6>14>2>13>16>12>5>18>20,表明20家分行中分行1的综合运营业绩最优,分行20的综合运营业绩最差。
6 结语
本文提出一种基于样本单元的区间数多属性综合评价方法。针对样本单元或决策单元的评价指标取区间数,或两者的评价指标均取区间数的情况,分别建立相对应的基于样本单元评价决策单元有效性的只有输出的广义区间DEA模型,并通过区间有效值对决策单元进行全排序和进一步的分类。与传统的数据包络分析方法相比,本文提出的方法,将传统DEA方法依据有效决策单元构成的评价参照系评价决策单元相对效率性拓展为依据任意参考集进行决策单元“非效率评价”在内的更具广泛含义的DEA方法,并将传统综合评价中的指标点值扩展到区间值进行研究。文中建立的模型各有其一定的优越性和应用场景,可根据实际问题选择不同类型的模型。
