足式机器人在非结构地形中的姿态求解算法

，，

(1.天津商业大学 机械工程学院，天津 100081； 2.北京理工大学 机电学院，北京 100081)

0 引言

仿生机器人一直是机器人领域的研究热点，足式机器人是其中的重要组成部分[1]。随着 “Big Dog”和 “Wild cat”等液压驱动机器人的出现，在野外环境应用的足式机器人逐渐增多，因而对适应非结构地形的姿态求解算法进行研究具有重要意义。机器人的姿态求解是指对机体相对于重力方向的俯仰角和横滚角进行求解。陀螺仪、加速度计等惯性测量单元(IMU)广泛地应用于飞行器的姿态求解中[2-3]，近年来也开始在足式机器人中使用。P.C.Lin等[4]在研究RHex六足机器人时，最早提出将机器人运动学与IMU相结合用于足式机器人的姿态解算。这种方法只适用于在平地上运动的机器人，并且要求机器人在任意时刻至少有三条腿与地面接触，具有较大的局限性。为了对四足机器人在平地上的姿态进行求解，S.P.N.Singh等[5]通过在机器人机体上设置三个距离传感器，获得机体与地面之间的相对位姿关系，并将其与IMU进行融合以获得最终的位姿。M.Reinstein等[6]提出了一种基于经验的姿态求解算法，利用关节编码器、压力传感器的信息得到实时步长，并将其作为量测向量对IMU的求解结果进行补偿，实现了机器人的姿态和速度的估计。由于足端与地面之间的相对滑动会大大降低算法的精度，因而要通过试验以确定补偿滑动的参数。以上方法仅解决了足式机器人在平地运动中的姿态求解问题，不能在非结构地形中使用。为此本文提出了一种新型的姿态求解算法，采用卡尔曼滤波器将机器人动力学与IMU相融合，实现了足式机器人在非结构地形中的姿态求解。

1 机器人的动力学分析

如图1所示，在机器人的运动空间建立惯性坐标系I，并在机体质心处建立机体坐标系B。机体受到的合力包括重力,腿部对机体作用力以及机体受到的外界冲击力。以坐标系B作为参考坐标系，机体所受合力可以用下式表示：

BFs=BFl+BFe+BG

(1)

式中,左上标B表示向量以坐标系{B}为参考坐标系，BFs为所受合力，BFl为腿部对机体作用力，BFe机体受到的外界冲击力，BG为机体所受重力。BFl可以用下式表示：

(2)

式中,m为机器人腿的数量，Bfi为腿i对机体的作用力。机体运动加速度Bac如下：

(3)

式中,M为机体的质量，Bg为重力加速度在系{B}中对应的向量。

图1 足式机器人模型

将机体视为杆件0并在腿部各杆件上建立坐标系。机器人腿i上杆件由机体到足端依次编号为杆件1，2…n。将杆件j的上关节编号为关节j，并将杆件j的坐标系{j}固定在关节j处。其中坐标系{1}各坐标轴与机体坐标系{B}各坐标轴平行。由图1可知，由于腿部通过关节1与机体相连，因而Bfi即为关节1受到的腿部作用力。腿足式机器人的每条腿都可以看作是以机体为浮动基座的串联机器人[7]。将牛顿-欧拉方程进行变形[8]，得到腿i的关节1受力Bfi的计算公式如下所示：

(4)

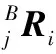
对于腿i来说Fi,j可以用下式所示：

(6)

(7)

2 姿态求解算法

2.1 机器人机体姿态的描述

机器人机体的横滚角(roll)、俯仰角(pitch)和偏航角(yaw)，分别为机体相对惯性坐标系x、y、z三个轴的旋转角度，其中横滚角和俯仰角称为机器人的姿态角。机体坐标系B与惯性坐标系I之间的变换关系可以采用方向余弦矩阵C表示：

(8)

式中,c代表cos，s代表sin，α、β和γ分别表示机器人机体的偏航角、俯仰角和横滚角。将C改写成如下形式:

(9)

注意到Z只包括β、γ两个变量，且形式较为简单，仅使用Z中的元素就能计算出横滚角和俯仰角，如下式所示：

(10)

2.2 卡尔曼滤波器设计

本文采用三轴陀螺仪和加速度计，建立传感器输出信号模型，如下所示：

(11)

yG和yA分别为陀螺仪和加速度计的输出信号，Bw为机体的角速度。nG和nA分别表示陀螺仪和加速度计的测量误差，均为零均值的高斯白噪声。

卡尔曼滤波器包括状态方程和量测方程[9]，如下所示：

(12)

其中:xt和zt分别为状态向量和量测向量，Φt,t-1为t-1时刻到t时刻的一步转移矩阵，Ht为量测矩阵，wt和vt分别为系统激励噪声和量测噪声。将状态向量xt定义为Z。下面分别确定状态方程和量测方程。

2.2.1 状态方程

卡尔曼滤波器的状态方程基于捷联式惯导算法[10]，如下所示：

Ct=Ct-1(I+Δt[ωt-1])

(13)

式中，Ct为t时刻的方向余弦矩阵，△t为时间间隔。[ωt-1]为ωt-1的斜对称矩阵。根据式(9)可以将式(13)整理成如下形式：

Zt=(I+Δt[ωt-1])ΤZt-1

(14)

由式(10)可知[ωt - 1]=[yG, t - 1]-[nG,t],且[ωt-1]=-[ωt-1]Τ，代入式(14)可得：

Zt= (I-Δt[yG ,t - 1])Zt - 1-Δt[Zt-1]nG,t-1

(15)

将式(15)和的状态方程中各部分相对应，可知Φt,t-1和wt可以用下式表示：

Φt ,t - 1=I-Δt[yG, t - 1]

wt-1= -Δt[Zt-1]nG

(16)

状态方程的噪声协方差可以定义为Qt-1=E(wt-1wt-1Τ)，式中E表示对变量求期望，将式(15)中的wt-1代入可得Qt-1的表达式：

Qt-1=Δt2[Zt-1]∑G[Zt-1]

(17)

式中,∑G是陀螺仪测量噪声的协方差矩阵，可以用E(nGnGΤ)表示。

2.2.2 量测方程

Bg=g×Z

(18)

将式(2)、(7)及(18)代入式(11)中的加速度计输出信号模型，并进行整理得:

(19)

其中:下标t表示各向量在t时刻的值。将式(19)与量测方程相对应，可知zt、Ht和vt的表达式分别如下所示：

(20)

与状态方程类似，量测方程噪声协方差矩阵Mt由Mt=E(vtvtΤ)定义。当BFe,t不存在时，Mt为nA的噪声协方差E(nAnAΤ)。当BFe,t存在时，量测方程会产生很大的量测误差，不能用于姿态求解，可以通过将噪声协方差Mt设为无穷大来实现，如下式表示:

(21)

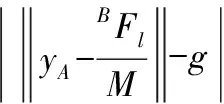
2.2.3 卡尔曼滤波器的参数确定

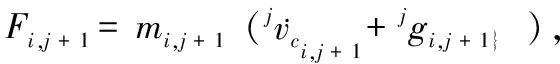
(22)

通过卡尔曼滤波器的递归运算就能获得Z的估计值，再通过(10)式的计算就得到横滚角β和俯仰角γ。整个姿态求解算法的流程如图2所示。

图2 姿态求解算法的流程图

3 仿真和算法验证

3.1 仿真条件设置

ADAMS是一款出色的虚拟样机仿真软件，在对机构进行仿真的过程中，ADAMS能够获得各构件任意点的速度、角速度、方位角等运动学参数和力、力矩等动力学参数，并且可以将这些参数在不同的坐标系下进行表示，因而在本文中使用ADAMS进行仿真实验以对提出算法进行验证。在本文中选取了两款典型的足式机器人的简化模型进行仿真(如图3所示)，其中四足机器人具有与哺乳类动物类似的腿部结构，六足机器人具有与昆虫类似的腿部结构，两款机器人腿部都由三个杆件组成，杆件之间采用旋转关节进行连接，但关节采用不同的布置方式。机器人机体采用钢制材料，腿部采用铝制材料，各杆件的质量和尺寸参数如表1所示。

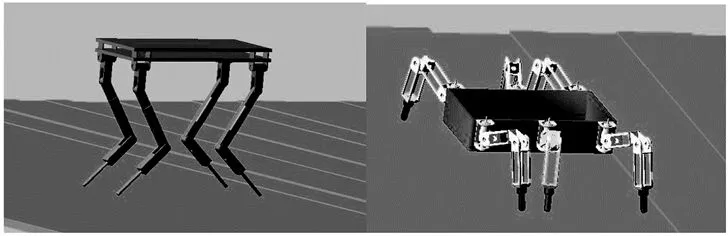
图3 仿真中使用的足式机器人

如图3所示，在仿真中使用不规则的阶梯地面作为非结构地形，其中每个阶梯的长度范围为160～300 mm，高度范围为10～40 mm，相邻阶梯随机凸起或凹陷。在仿真中四足机器人采用对角步态(对角两腿同时抬起或着地)，六足机器人采用三角步态(不相邻的三腿同时抬起或着地)沿直线运动。仿真共进行三组，具体的条件设置如表2所示。

表1 机器人的结构和尺寸参数

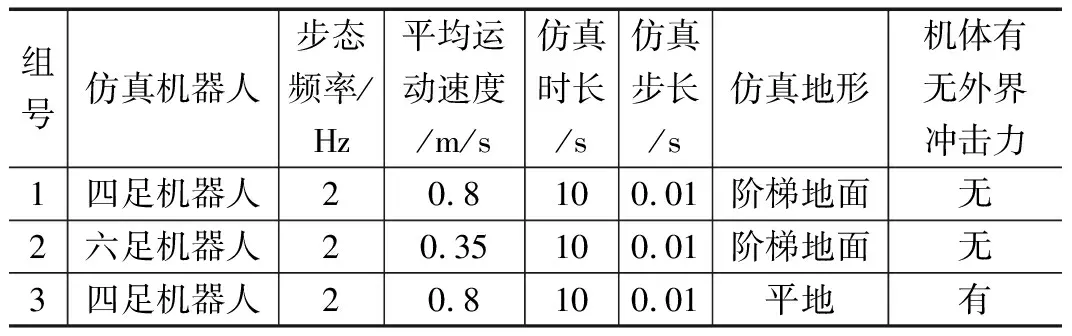
表2 仿真实验的条件设置

在前两组仿真中，两款机器人分别在阶梯地面上运动。机器人开始运动时阶梯地面较为平缓，随着运动的进行，阶梯高度的变化越来越剧烈。由于在阶梯地面运动时，机器人很容易倾倒，因而前两组仿真中没有给机器人机体施加外界冲击力。 为了检验机器人机体受到外界冲击时算法的效果，在第3组仿真中四足机器人在平地上运动，在保证机器人不倾倒的情况下，对机体Y轴正方向施加了如图4所示的冲击力。

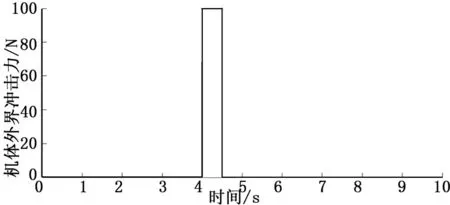
图4 机器人机体外界冲击力

3.2 数据处理分析

根据上节所示设置的条件进行仿真后，进行数据采集，数据的采样频率为100 Hz。这些数据包括机体的真实俯仰角和横滚角(用于与计算值对比)、角速度、加速度、方向余弦矩阵，各杆件质心的加速度和方向余弦矩阵，关节角度及足端冲击力等。根据关节角度采用D-H法可以得到各杆件坐标系到机体坐标系的旋转变化矩阵。采用文献[12]的方法，根据关系传感器信号的特点，在真实值的基础上加上高斯白噪声来模拟惯性传感器输出信号。算法中使用的陀螺仪的输出为在角速度基础上加上协方差∑G=0.056I的零均值高斯白噪声，各加速度计的输出信息则是在运动和重力加速度之和的基础上加上协方差∑A=0.03I的零均值高斯白噪声。各杆件坐标系下的重力加速度用向量[0 0 g]T与杆件的方向余弦矩阵的乘积获得。

在对采集的信息进行处理后，使用本文提出的算法对姿态角进行计算，结果如图5、图6所示。从图中可以看出，在前两组仿真开始时，由于地面较为平缓，两款机器人姿态角比较稳定。随着运动的进行，阶梯变化越来越剧烈，姿态角的变化也越来越大。但整个仿真过程中姿态角计算值始终能够准确反应真实值的变化。由于这两款具有不同的结构，并采用不同的步态运动，说明算法具有较好的通用性。在第3组仿真中，当机体冲击力存在时，只能依靠陀螺仪进行姿态求解，由于用陀螺仪的角速度求解姿态时需要积分，噪声在积分后产生了较大的计算偏差。当冲击力消失后，加速度的信息又能用于姿态求解，从而使计算偏差迅速减小。从图6中可以看出，即使在冲击力存在的情况下，计算值的偏差仍能控制在较小水平，能够满足机器人平衡控制的需要。

图5 姿态角计算结果

图6 姿态角计算偏差

4 结论

针对以往机器人姿态求解方法存在的不足，提出了一种适用于非结构地形的姿态求解方法，该算法通过动力学分析得到机器人机体运动加速度，并将其引入到卡尔曼滤波器的量测方程中，通过与惯性测量单元(IMU)的信息相融合来获得准确的姿态信息。通过两款典型的足式机器人在非结构地形中的仿真分析，验证了所提算法的有效性和通用性。与之前研究相比，本文提出的方法具有以下特点：

1)提出的算法采用动力学与IMU相结合的方法，将惯性传感器、力传感器和角度传感器等多传感器的信息相融合，实现了足式机器人在非结构地形中的姿态求解。

2)当机体存在外界冲击力作用时，算法的计算值偏差将会增大，但仍能保证平衡控制的需要，当冲击力消失后，计算值的偏差又将迅速变小。