天然裂缝多孔介质中流体运移的流线模拟

左立华，于伟 ，苗继军，VARAVEI Abdoljalil，SEPEHRNOORI Kamy

（1. College of Business, Engineering and Technology, Texas A&M University-Texarkana, Texarkana, TX 75503, USA;2. Department of Petroleum Engineering, Texas A&M University, College Station, TX 77843, USA; 3. Department of Petroleum and Geosystems Engineering, University of Texas at Austin, Austin, TX 78712, USA; 4. SimTech LLC, Austin, TX 78751, USA）

0 引言

利用EDFM可以准确地计算油藏压力分布和流体流量，但是压力分布并不能准确地描述复杂的裂缝网络和流体流动轨迹。为了优化水驱方案，需要采用流线模拟方法计算流体流动轨迹和流动时间[20-23]，由于双孔双渗方法模拟裂缝的局限性，之前的流线模拟不能像EDFM那样很好地模拟流体流量和裂缝的几何结构[24-25]。

本文结合 EDFM 和流线模拟方法，开发了一套新的数值模拟方法来计算流体在基质和裂缝中的流动轨迹，为优化水驱方案、提高水驱采收率提供技术支持。

1 数学模型

1.1 黑油模型中的EDFM

黑油模型广泛用于模拟油藏中的三相流动，而EDFM 可以准确模拟裂缝的几何结构，两者结合可以很好地模拟裂缝性油藏中的水驱过程[18]。使用 EDFM模拟复杂的裂缝系统已经被证明是可行的[19]。通过将裂缝离散为小的分段裂缝并嵌入到待计算区域中，EDFM 融合了双孔双渗方法和离散裂缝方法的优势。因此，EDFM可以避免非结构网格带来的高计算成本，同时又能保留油藏模拟器本身的优势。

1.2 流线模拟方法

流线模拟技术已经被广泛地应用于计算油藏流体流动轨迹和流动时间。Muskat[21]首先利用流线和流管研究流体运移的问题，在此基础上，许多研究人员使用流线方法来模拟简单的水驱问题[26-28]，并对二维空间不可压缩流体适用的势函数和流线函数进行定义。流线的“飞行时间”作为空间变量引入之后[29]，饱和度的运移方程便可以沿着流线进行数值求解，从此流线模型逐渐代替了流管模型。流线算法随着非常规油气储集层中裂缝模拟技术的进步而逐步改进。Pollock[23]建立了针对矩形网格计算流线轨迹和流动时间的经典方法，随后该方法被扩展到复杂的三维油藏结构中[30-31]，进而通过引入基于角点网格的拟飞行时间对该方法做进一步简化[32]。对于流线方法在非结构网格、断层网格和局部网格中的应用，有许多学者通过引入局部边界层的方法来处理交界面上的流速不连续问题[33-35]。

流线模拟在天然裂缝性油藏中的应用存在 2个棘手的问题：①由于裂缝的存在，流线模拟需要计算两侧具有不同精度交界面上的流线轨迹；②油藏模拟器计算得到的基质和裂缝网格上的流量对于流线模拟来说并不够。新的局部边界层的方法可以解决第 1个问题[32-35]。为了解决第 2个问题，本文利用已知基质和裂缝流量，基于质量守恒定律来计算三维网格 6个面的流量。

二维情形下只有 1条裂缝的基质网格中体积流量的关系见图1。基质被裂缝分成2个小的基质网格，假设基质网格的流量为f1—f6、裂缝网格的流量为f7—f10，其中f7和f8是基质网格和裂缝网格共享的。假设f3+f4+f9=F1、f5+f6+f10=F2、f7+f8=F3，引入 EDFM 方法的油藏模拟器可以计算基质网格每个面上的流量（f1、f2、F1、F2）、裂缝网格上的流量（f9、f10）以及裂缝和基质网格之间的总流量F3。对于流线模拟来说，每个新网格所有6个面的流量也需要额外进行计算。

2.1.10 铁。2012年全市叶片铁平均含量为146.16 mg/kg(表1)，说明铁的含量在较高的水平，这与果园较低的土壤pH有关。烟台果园土壤通常不缺铁，土壤中的过量磷和有机质能够降低铁的有效性。土壤铁含量过高影响阳离子交换量和降低其他养分的有效性。

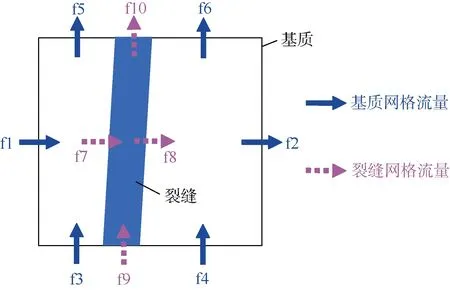
图1 二维网格中裂缝流量与基质流量关系图

在本文研究的所有案例中，最下方一面裂缝的流量占那一侧流量的大部分，因此可以假设f3=f4、f5=f6，联立所有流量关系得到如下方程组：

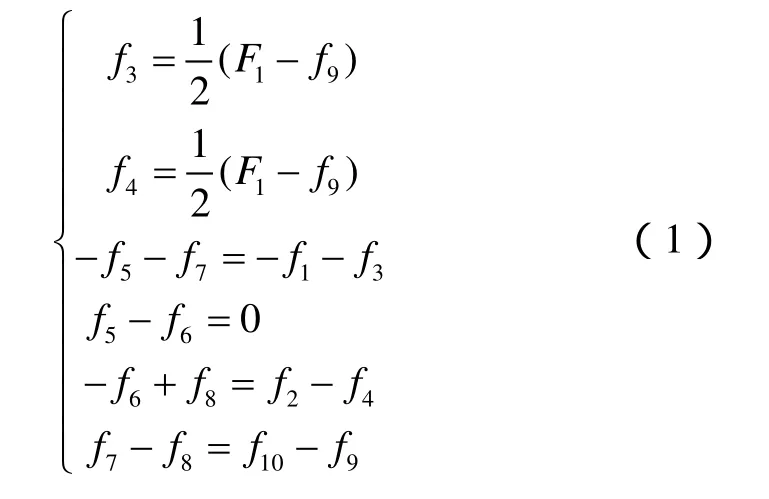
在（1）式中，F1、f1、f2、f9、f10均为已知，可以直接计算f3=f4=1/2（F1－f9），（1）式可以改写为：

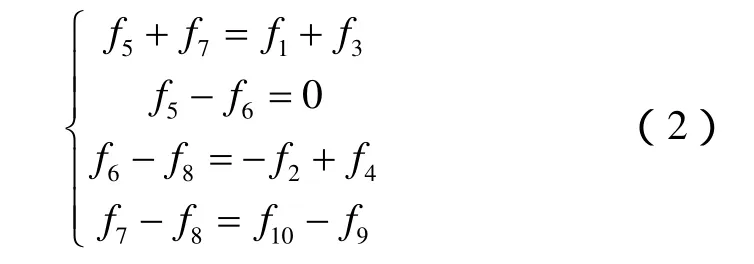
将它写成线性系统如下，

其中

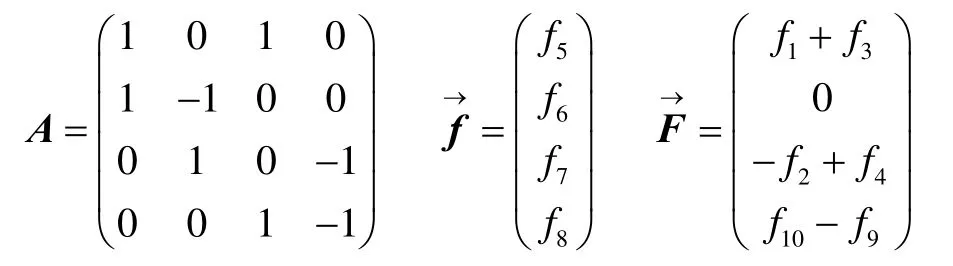
求解（3）式便可得到流线模拟所需要的全部基质网格和裂缝网格流量。对于与裂缝相交的井筒网格，在油藏模拟器计算出井筒网格的流量之后，流线方法会把井筒网格与其他网格一样处理。

2 模型应用

2.1 模型假设

假设有一天然裂缝性油藏，注水井位于油藏西南角，生产井位于油藏东北角。为了集中分析流体在天然裂缝中的流动机理，避免裂缝和基质相交造成的复杂结构的影响，假设天然裂缝互不相交，走向角为 0°或者90°。假设裂缝渗透率与基质渗透率相差很大，裂缝与油藏边界不相交，流体为不可压缩流体，流动遵循达西定律。

2.2 模型描述

油藏模型尺寸为152.4 m×152.4 m×6.1 m，划分为20×20×1共 400个网格，所有网格具有相同尺寸 7.62 m×7.62 m×6.10 m。以0.000 18 m3/s速度恒定注水，生产井的压力为6.89 MPa。模型基本参数见表1。

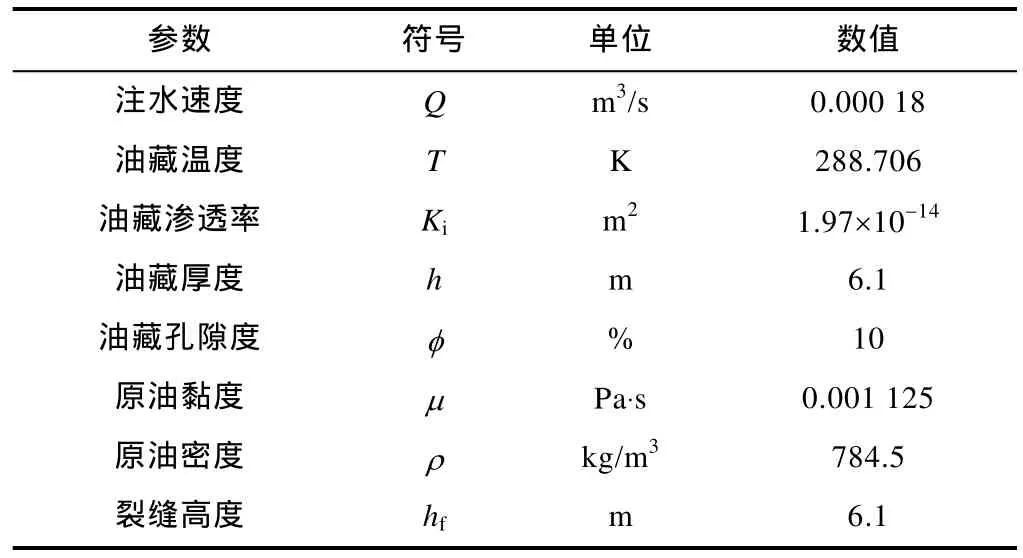
表1 模型基本参数

2.3 模型验证和模拟效率

为了显示基于EDFM的流线模拟的准确性，将流线轨迹和飞行时间值与含水饱和度结果进行了比对（见图2）。生产600 d后的含水饱和度结果（见图2a）与流线轨迹和飞行时间值（见图2b）具有很好的一致性。

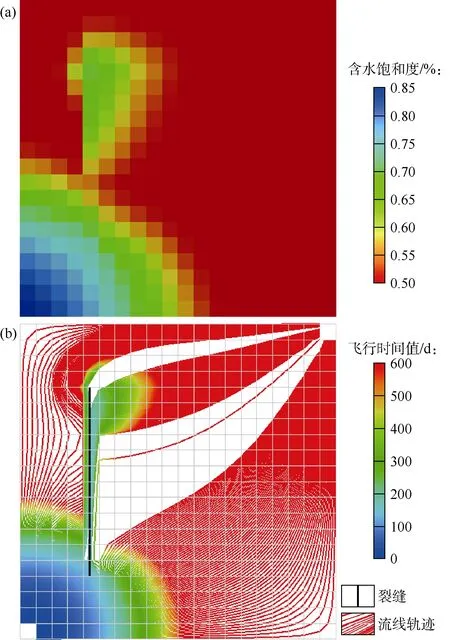
图2 含水饱和度结果（a）与流线轨迹和飞行时间值（b）对比图

在重建几何关系和相邻关系的基础上，利用流线算法计算每条流线的轨迹以及流线上流体流动时间。每条流线都是独立计算，为将来的并行计算节省时间。计算时间的长短主要取决于网格数量，随着额外裂缝网格的引入，会增加计算时间。对于无裂缝的均质油藏，油藏模拟器的计算时间为 75 s，流线模拟的计算时间为240 s；对于裂缝性油藏，油藏模拟器的计算时间为120 s，流线模拟的计算时间为300 s。可以看出，额外裂缝网格的增加会增加计算成本，但是在同等精确度的情况下，本文方法的计算效率较高。

2.4 案例研究

2.4.1 无裂缝均质油藏

无裂缝均质油藏（0号模型）的计算结果显示（见图3），流线模拟可以将无裂缝均质油藏水驱流体的分布情况清楚地刻画出来，因为油藏是均质的，所以水驱前沿均匀推进。

2.4.2 裂缝导流能力对流动轨迹和流动时间的影响

为了研究裂缝导流能力对流动轨迹和流动时间的影响，设定了高、低2种裂缝导流能力（见图4）。在油藏左边存在1条长度为83.8 m的垂直裂缝，裂缝导流能力分别设定为 7.52×10-9m2·m（1号模型）和7.52×10-11m2·m（2号模型），生产1 000 d时的流线轨迹和飞行时间值的分布如图4所示。

当裂缝导流能力为7.52×10-9m2·m时，水驱前沿到达裂缝之前，驱替流体均匀推进，当水驱前沿到达裂缝时，流速突然增加，在生产1 000 d的时候，经过裂缝流动的水驱前沿已经接近到达生产井，而其他部分刚刚推进到了离注水井118 m的地方（见图4a）。图4a显示一方面裂缝可以作为流体的快速通道，另一方面流体只能在裂缝附近流动而不能到达远离裂缝的地方，裂缝又起到了“屏障”的作用。与图3相比，图4a中出现被油藏工程师称为“死区”或者“阻塞区”的空白区域，该区域的存在会减少驱扫体积，降低水驱采收率。为了避免过早见水，可以采取注入凝胶和纳米颗粒等方法来延缓通过裂缝快速流动的水流。

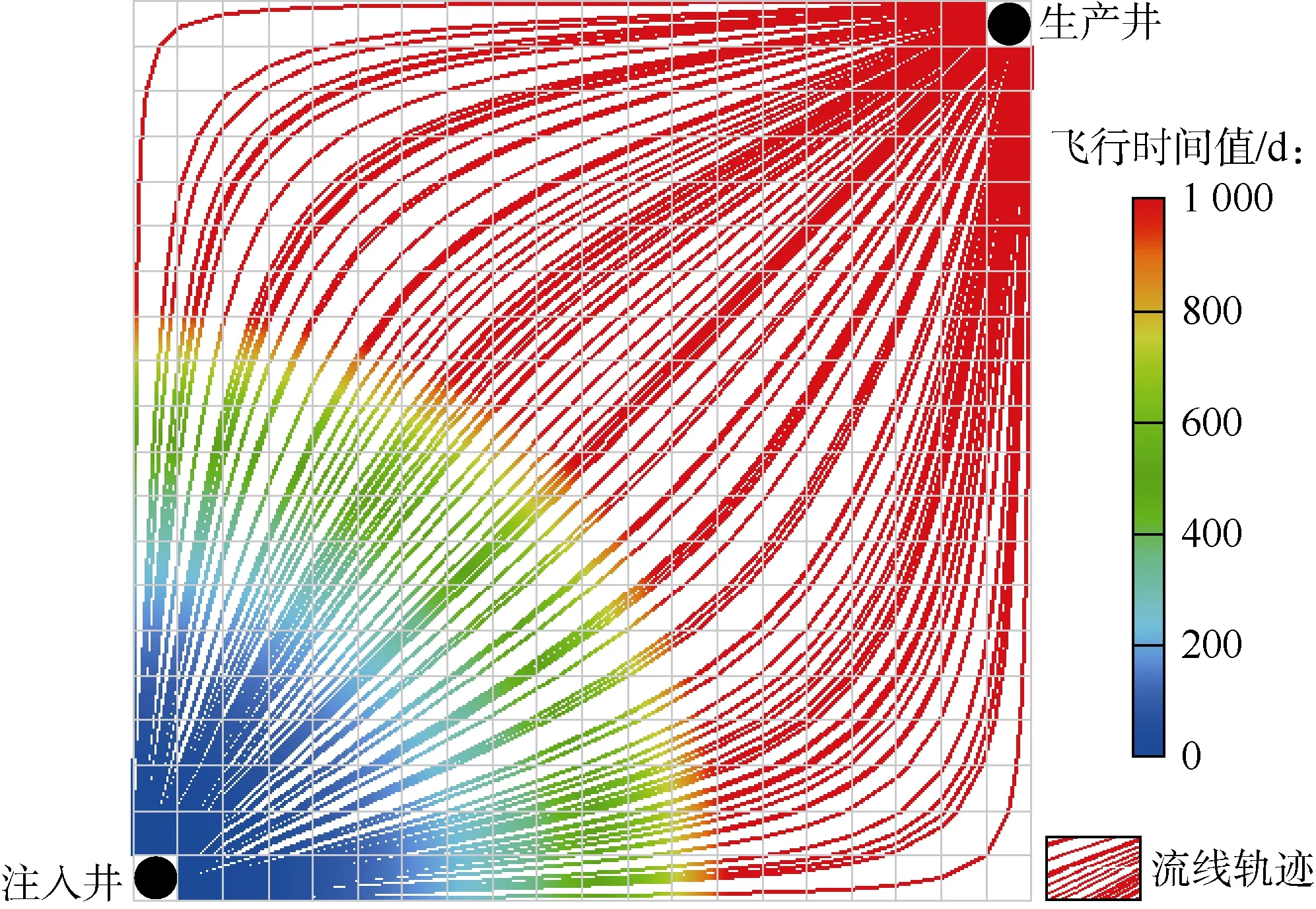
图3 无裂缝均质油藏流线和飞行时间值计算结果

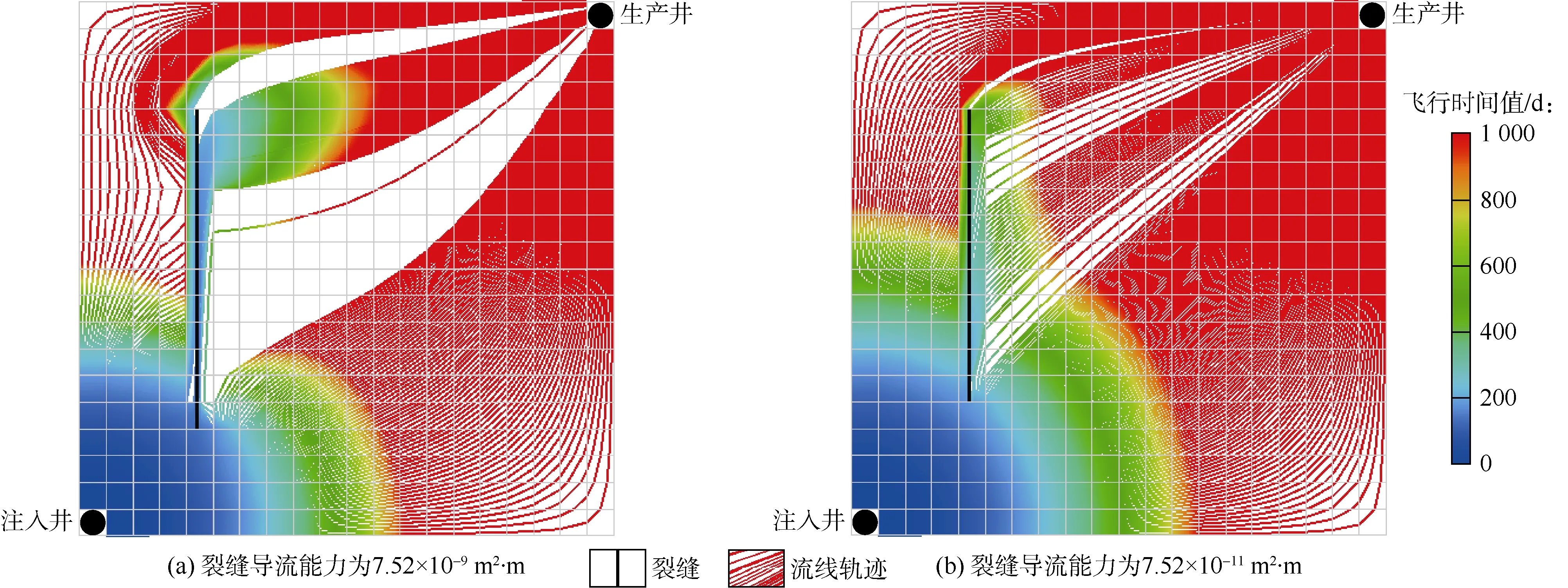
图4 不同裂缝导流能力下的流线轨迹和飞行时间结果

在生产1 000 d的时候，高裂缝导流能力的水驱前沿到达了距离裂缝上端38.1 m的位置（见图4a），而低裂缝导流能力的水驱前沿只到裂缝上端15.2 m的位置（见图4b）。随着裂缝导流能力的减小，裂缝的“快速通道”作用和“屏障”作用也相应减弱，有更多的水流可以穿过裂缝到达另一侧，从而减小了“死区”体积。

2.4.3 裂缝数目对流动轨迹和流动时间的影响

为了研究裂缝数目对流动轨迹和流动时间的影响，设定了3条裂缝（3号模型）和12条裂缝（4号模型）2种裂缝数目模型（见图5）。其中3条裂缝模型的裂缝长度分别为83.8 m、76.2 m和68.6 m，相应的流线轨迹和飞行时间分布显示，一部分水流被第 1条裂缝改变路径的同时，仍有一部分水流穿过第 1条裂缝，随后被第2条裂缝改变轨迹。第2条裂缝的“屏障”功能比第 1条裂缝弱一些，不过“快速通道”的功能还是很明显。第3条裂缝的“屏障”功能相比第2条裂缝弱一些（见图5a）。12条裂缝模型的流线轨迹和飞行时间分布显示，随着裂缝离注水井的距离越来越远，“快速通道”作用越来越弱（见图5b）。

2.4.4 裂缝位置对流动轨迹和流动时间的影响

为了研究裂缝位置对流动轨迹和流动时间的影响，设定了3种裂缝位置的模型（见图6）。第1种裂缝位置模型（5号模型）包含垂直和水平2条裂缝，长度均为83.8 m，流线和飞行时间结果显示，水平裂缝与垂直裂缝具有同样的“快速通道”作用和“屏障”作用（见图6a）。第2种裂缝位置模型（6号模型）包含8条裂缝，流线和飞行时间结果显示，由于第1条垂直裂缝被分成了 2条短垂直裂缝，流线轨迹发生了明显的变化，更多水流得以穿过裂缝。另外，水平裂缝的存在提高了见水速度（见图6b）。第3种裂缝位置模型（7号模型）在第2种裂缝位置模型的基础上将上边第1条水平裂缝的位置下移9.1 m，流线和飞行时间结果显示，由于这条裂缝的位置下移，导致裂缝的“屏障”作用更加明显，进一步减少了驱扫体积（见图6c）。关于死区的定量分析对压裂方案设计和井位优化有所帮助。

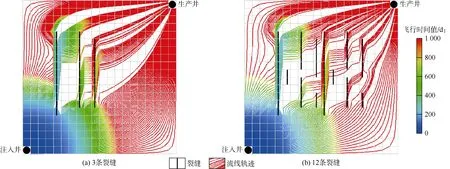
图5 不同裂缝数目的流线轨迹和飞行时间结果

图6 不同裂缝位置的流线轨迹和飞行时间结果

2.5 水驱效果分析

设计水驱方案时主要考虑见水时间和驱扫体积这2个因素。见水时间越晚，驱扫体积越大，水驱效果越好。目前见水时间是通过分析产水量的突变时间来确定，驱扫体积是通过研究压力或者含水饱和度分布来粗略确定，这种分析方法准确性较差。利用本文提出的流线技术，见水时间可以通过计算所有流线上水驱前沿到达生产井的最小时间来确定，这个步骤通过比较所有流线上的飞行时间值就可以完成，大大提高了准确性；驱扫体积可以通过累加至少有 1条流线通过的网格体积而近似得到。本文研究采用均匀网格，所有网格的体积相同，可以用驱扫网格数来代替驱扫体积，驱扫网格数除以总网格数即可得到驱扫效率。由此可以定量分析裂缝对水驱效果的影响（见表2）。

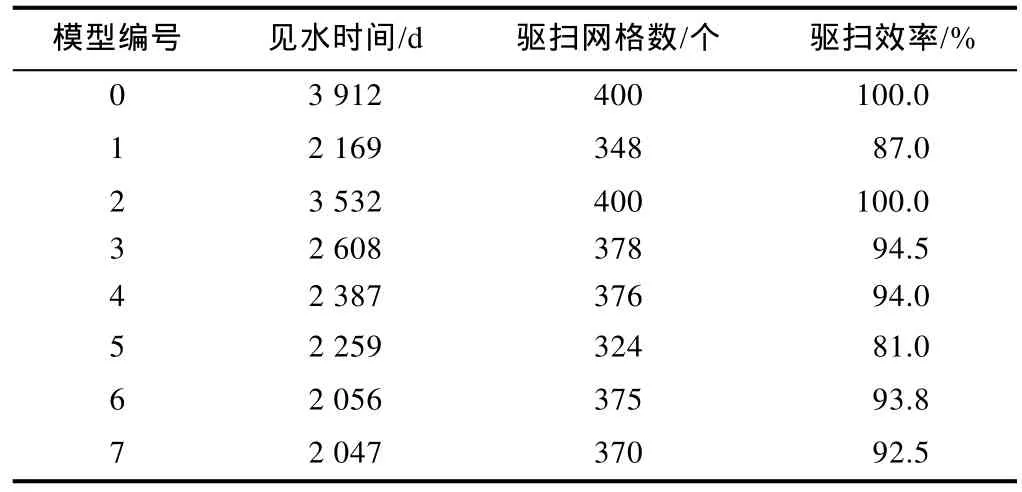
表2 见水时间和驱扫体积统计表

表2结果显示，随着裂缝导流能力的增高以及裂缝位置复杂程度的增加，见水时间加快、驱扫体积减少。裂缝数目对于流体流动轨迹和流动时间的影响不能一概而论，1号模型确实比0号模型见水时间快、驱扫体积少，但是5号模型比1号模型有更多的裂缝，见水时间却慢了 4%、驱扫体积减少了 7%。3号模型比1号模型多了2条裂缝，见水时间却慢了20%、驱扫体积增加了9%。在驱扫体积接近的情况下，4号模型的见水时间比3号模型快了8%，表明并不是垂直裂缝越多越好。在驱扫体积接近的情况下，4号模型的见水时间比6号和7号模型慢了近17%，表明两组裂缝会比单组裂缝具有更快的见水时间。7号模型和6号模型的唯一差别是 1条水平裂缝的位置，但是驱扫体积却差了1%，表明裂缝的位置对流体流动轨迹和流动时间的影响较大。

3 讨论

天然裂缝性油藏中的水驱模拟对于理解流体在裂缝中的运移和评估水驱效果从而达到最好的经济效益尤为重要。由于裂缝模拟的复杂性，研究裂缝型油藏中水驱效果的结果非常少。大多数研究使用的是双孔双渗模型来模拟裂缝，因为自身固有缺点，模拟的精确度不高。

本文将EDFM强大的模拟裂缝能力与流线方法计算流体轨迹和流动时间的准确性相结合，通过定量计算水驱前沿的流动轨迹和流动时间，对天然裂缝性油藏中裂缝的导流能力、裂缝数目和裂缝位置对水驱效果的影响进行研究。为了集中研究裂缝对流动机理的影响，对裂缝性质进行了简化。本文中提出的技术经过拓展，可以辅助油藏工程师进行注水速度的优化和新井位置的选取。

本文中所有的裂缝都是二维的，具有相同的高度，因此重力的影响可以忽略不计。为了集中研究某一个瞬时时间的流线结果而忽略了时间效应。对于实际油藏来说，重力和时间效应予以考虑。另外，本文中的裂缝都是人为设置的，而实际油藏中的裂缝结构更加复杂，需要对本文中提出的技术做进一步改进，从而能够更准确地进行流线模拟。

4 结论

在其他条件相同的情况下，与无裂缝的均质油藏相比，裂缝性油藏中水驱见水时间会快 30%，而驱扫体积会少10%。虽然增加单条裂缝可以加速见水时间，减少驱扫体积，但增加更多裂缝却不一定得到相同效果。水驱效果还跟裂缝的走向和位置有关系，不同的走向和位置可以导致见水时间相差 20%，而驱扫体积相差9%。裂缝长度越短，对于流体流动轨迹和流动时间的影响越小。裂缝的位置对驱扫效率影响较大，单条裂缝的位置变动可以导致驱扫体积变化1%。