不同风险偏好组合下的供应链订货策略
2019-03-04李常洪
魏 恒,李常洪
(山西大学 经济与管理学院,山西 太原 030006)
一 引言
经典的经济学假设决策者完全理性,决策时对风险持中性态度。自前景理论被提出后,更多学者考虑决策者的风险偏好来解释实践中的经济管理问题。现有文献主要从三个角度研究决策者的风险偏好对供应链协调和绩效的影响。第一类是从制造商或供应商风险偏好的角度展开,如李刚等[1]考虑供应商风险规避,提出了一套基于实物期权的契约来协调供应链;曹晓刚等[2]也假定制造商规避风险,构建了多级闭环竞争型供应链网络,通过均衡求解分析了风险偏好、回收系数和再制造率对均衡结果的影响,表明制造商的风险决策偏好对企业利润和订购量有显著影响。第二类则考虑零售商的决策偏好,马利军等[3]研究了风险厌恶型零售商的供应链合作博弈;史成东等[4]构建了销售商风险规避情形下的闭环供应链协调模型;丁松和但斌[5]则考虑零售商的决策风险偏好对最优订购策略的影响,并将其应用于农产品供应链上;徐志春[6]针对零售商风险厌恶,提出了一套更具柔性的实物期权契约来协调供应链;许民利等[7]在研究供应链协调与优化时,在考虑零售商风险厌恶的基础上增加了努力因素对协调模型的影响,并给出了实现协调的各契约参数的满足条件;郭金森等[8]同样针对风险厌恶型零售商,研究资金约束下的双渠道供应链运作和协调策略;张新和罗新星[9]则考虑零售商的损失厌恶偏好,研究了供应链商业信用和收益共享协调模型。第三类同时考虑了供应商和零售商的风险偏好,庞庆华[10]先考虑了供应商和零售商不同时具有浪费厌恶偏好的供应链契约,供应商厌恶浪费时,其批发价和收益份额会因其浪费厌恶的增加而减小;零售商厌恶浪费时,供应商的批发价格和收益会随着零售商浪费厌恶的增加而增加;庞庆华[11]又研究了供应商和零售商分别厌恶缺货的供应链收益共享契约,发现零售商具有缺货厌恶偏好时,随着缺货厌恶的增加,供应商所提供的批发价、所获收益份额也会增加;供应商厌恶缺货时,随着缺货厌恶的增加,供应商所提供的批发价、所获收益份额会减小。但这些文献[10-11]未考虑缺货成本,所引入的协调契约是收益共享契约,忽略缺货成本来研究缺货厌恶和浪费厌恶偏好对供应链绩效的影响本身有明显的缺陷,甚至出现无法协调的问题。Wu等[12]假设面对随机产能,通过VaR和CVaR模型比较了供应链成员在不同风险偏好类型下的库存优化决策;张新鑫等[13]在此基础上分析了CVaR准则下的供应链优化问题,重点探讨了规避程度对绩效的影响;叶飞等[14]考虑决策者偏好特性,利用CVaR对供应链定价与竞合策略作了探讨,表明决策者偏好对最优定价与合作策略有关键的影响;甘信华和应可福[15]考虑供销两侧都厌恶风险时的VMI协调问题,通过CVaR模型实现了供应链完美协调。
上述第一类和第二类的文献较多,即针对单一节点企业的决策者偏好研究供应链协调模型及应用,且偏好类型大多是针对损失厌恶或风险规避型,第三类同时考虑供应商和零售商决策偏好的文献较少。Schweitzer和Cachon[16]将风险偏好分为风险中性、损失厌恶、缺货厌恶、浪费厌恶、风险喜好等8种,但目前较少有文献研究缺货厌恶、浪费厌恶等风险偏好,有少数学者研究了单个节点的缺货厌恶或浪费厌恶偏好并作了比较分析,本文所考虑的风险偏好正是缺货厌恶和浪费厌恶两种。
另外,上述文献大多采用了收益共享契约,但在考虑风险偏好尤其是缺货厌恶和浪费厌恶时,收益共享本身有一定的弊端,因此从20世纪90年代开始,学者们提出并运用回购契约来探讨决策者风险态度对供应链的影响。Eeckhoudt和Gollier[17]从库存水平的角度探讨了管理者的风险态度对其决策行动的影响。Lau H和Lau A H[18]通过数值实验证明风险厌恶型制造商给出的最优价格和回购价格比风险中性时更低,对风险中性的零售商所提供的回购价格接近于零。Agrawal和Seshadri[19]考虑了一个供应商和多个风险厌恶型零售商组成的单周期供应链,结果表明零售商可通过共享契约实现风险的共担,提高订购水平。Tsay[20]探讨了供应链成员的风险态度对回购契约的影响,认为供应商和零售商的风险态度对回购契约参数的影响是矛盾的,这也就说明了为什么实际中某些行业不会采用这种契约形式。Choi等[21]构造了同时具有风险厌恶偏好的供应商和零售商组成的供应链,考虑整体优化问题,结果表明,在集中式供应链中回购价格的变化会影响利润再分配和风险的分摊。Ohmura[22-24]拓展Tsay[20]的模型:文献[22]构建了风险中性的制造商和风险厌恶的零售商组成的供应链,分析了零售商的风险厌恶程度对供应链绩效的影响;文献[23]在此基础上通过数值实验证明了均值方差和VaR两种不同的风险度量方式对绩效的影响是不同的;文献[24]进一步研究了制造商和零售商同时有较高或较低的风险厌恶态度对退货策略的影响,结果表明制造商的风险敏感性对回购契约和供应链绩效的影响更为突出。
总之,(1)从风险偏好类型上看,已有文献大多单独考虑一种偏好,如文献[1-9]针对成员损失厌恶偏好,文献[10-11]是针对缺货厌恶和浪费厌恶,该方面的研究比较有限,同时考虑两种风险偏好组合的研究则更少;(2)大多文献只考虑供应链某一成员节点的风险偏好,同时考虑两个决策者风险偏好的文献涉及较少;(3)从契约类型的角度看,大多已有文献是从收益共享契约或批发契约的角度展开,从回购契约展开并考虑决策者风险态度的研究并不多。
本研究与已有文献不同:(1)一般文献较少同时考虑两种风险组合,并且针对浪费厌恶偏好的研究较少,本文则同时考虑决策者缺货厌恶和浪费厌恶两种偏好,分析了四种不同偏好组合下的供应链绩效,更加符合实际,可以解决不同风险偏好组合和厌恶程度下供应链成员的管理决策问题,具有一定的管理实践性;(2)本文同时考虑了供应商和零售商两个供应链节点成员的风险偏好,而已有文献大多只针对供应商或零售商即单一成员;(3)考虑回购契约,因其与收益共享和批发价格契约相比,更加适用于缺货厌恶和浪费厌恶的供应链优化和协调模型,更能突出这两种偏好组合对供应链绩效的影响,更好地指导实践决策。
本文的主要贡献在于:基于供应链的决策主体(供应商和零售商),考虑两个决策主体的四种缺货厌恶和浪费厌恶的风险偏好组合,并针对四种风险偏好组合引入回购契约构建了四个博弈模型,求得了均衡解,最后分析比对了不同偏好组合下决策者缺货厌恶和浪费厌恶对零售商订货策略和供应商定价策略的影响。
二 问题描述和基本模型
研究对象为单一供应商(s)和单一零售商(r)构成的二级供应链系统。一般认为供应链成员因谈判力、市场地位、议价能力和信息掌握程度等不同而拥有不同的主导和跟随地位,在本文的Stackelberg博弈中以供应商为核心企业,零售商为追随者。具体的博弈过程为:零售商根据市场需求预测向上游供应商发出订单,供应商按一定的批发价格向下游零售商销售单一产品,零售商按市场价格将产品销售给消费者,在销售季节结束后,供应商以协议价格回购剩余产品。其中,实际的市场需求是随机的,产品有一定的时令性。假设产品的需求分布、市场价格等有关信息是完全对称的。
涉及的有关符号说明如下:下标s、r分别表示供应商、零售商的有关参数;p为单位产品的零售价格;c为单位产品的生产成本;w为单位产品的批发价格;v为销售结束后单位产品的残值;Q为订购量;b为单位剩余产品的回购价格,b满足回购契约的基本条件;g表示单位缺货成本;x为产品的随机需求量;f(x)、F(x)分别为需求量x的概率密度函数和分布函数;μ是需求量的均值;S(Q)表示销售期内产品的期望销量;I(Q)表示产品的期望剩余量;L(Q)表示产品的期望缺货量。由上述假设可得到:
I(Q)=E(Q-x)+=Q-S(Q)
L(Q)=E(x-Q)+=μ-S(Q)
(一)集中式决策下的供应链协调模型
集中式决策下,整个供应链系统相当于一个整体企业,目的是使整个供应链系统绩效最优。假设πt(Q)、πs(Q)和πr(Q)分别表示供应链系统、供应商和零售商的期望利润,则零售商的期望利润为:
πr(Q)=pS(Q)+bI(Q)-wQ-grL(Q)
=(p-b+gr)S(Q)-(w-b)Q-μgr
供应商的期望利润为:
πs(Q)=wQ-cQ+(v-b)I(Q)-gsL(Q)=
(b-v+gs)S(Q)+(w-c+v-b)Q-μgs
供应链系统整体的期望利润为:
πt(Q)=πr(Q)+πs(Q)=
(p-v+g)S(Q)-(c-v)Q-μg
其中,g=gr+gs。
根据莱布尼茨法则,显然πt(Q)是关于Q的凹函数,令其一阶导数dπt(Q)/dQ=0,可求得供应链系统的最优订购量为:
(1)
可见,Q*是通过回购契约实现供应链最优绩效目标的最优订购量。集中式决策可作为分散式决策下的参照标杆。
为分析这两种偏好组合下决策者风险态度对供应链绩效和协调过程的影响,理论上可构建四类情形,如表1所示。

表1 成员风险偏好组合
接下来构建并分析四种不同偏好组合下供应链回购契约模型。
(二)零售商有缺货厌恶偏好,供应商有浪费厌恶偏好(S-W)
假设β1(β1>0)和λ1(λ1>0)分别是零售商单位产品的缺货厌恶系数和供应商单位产品的浪费厌恶系数,β1和λ1越大表示相应供应链成员的缺货或浪费厌恶程度越高。同时假设Ur1(πr(b))为零售商有缺货厌恶偏好时的效用函数,Us1(πs(b))为供应商有浪费厌恶偏好时的效用函数。此时可得到回购契约下零售商与供应商的期望效用如下:
E[Ur1(πr(b))]=pS(Q)+bI(Q)-
(p-b+gr)S(Q)-(w-b)Q-μgr-
(2)
E[Us1(πs(b))]=wQ+vI(Q)-bI(Q)-cQ-
=(b+gs-v)S(Q)+(w-c+v-b)Q-
(3)
命题1E[Ur1(πr(b))]是关于Q的凹函数,存在唯一的Qr1使取得最大值,且
(4)
证明:对式(2)求导数可得:
dE[Ur1(πr(b))]/dQ=
(p-b+gr+β1)(1-F(x))+b-w
(5)
d2E[Ur1(πr(b))]/dQ2=
-(p-b+gr+β1)f(x)<0

命题2E[Us1(πs(b))]是关于Q的凹函数,存在唯一的Qs1使E[Us1(πs(b))]取得最大值,且
(6)
证明类似命题1。

(7)
推论1当零售商有缺货厌恶偏好而供应商有浪费厌恶偏好时,零售商的最优订货量是其缺货厌恶偏好的增函数,供应商的批发价格是其浪费厌恶偏好的增函数。
推论表明:当零售商厌恶缺货供应商厌恶浪费时,供应链核心成员供应商为降低浪费风险,所给出的批发价格随其浪费厌恶程度的增大而增大,同时零售商的采购策略也随其缺货厌恶偏好的增强而变得更激进。这一结论也与实际情形相符。
(三)零售商有浪费厌恶偏好,供应商有缺货厌恶偏好(W-S)
假设β2(β2>0)和λ2(λ2>0)分别是零售商单位产品的浪费厌恶系数和供应商单位产品的缺货厌恶系数,β2和λ2越大表示相应供应链成员的缺货或浪费厌恶程度越高。并假设Ur2(πr(b))为零售商有浪费厌恶偏好时的效用函数,Us2(πs(b))为供应商有缺货厌恶偏好时的效用函数。此时零售商与供应商的期望效用如下:
E[Ur2(πr(b))]=pS(Q)+bI(Q)-
=(p-b+gr)S(Q)-(w-b)Q-
E[Us2(πs(b))]=wQ+vI(Q)-bI(Q)-
=(b+gs-v)S(Q)+(w-c+v-b)Q-
命题3E[Ur2(πr(b))]是关于Q的凹函数,存在唯一的Qr2使E[Ur2(πr(b))]取得最大值,且
命题4E[Us2(πs(b))]是关于Q的凹函数,当满足w-c≤b-v时,存在唯一的Qs2使E[Us2(πs(b))]取得最大值,且
同样,得到供应商的批发价格:
推论2 当零售商有浪费厌恶风险偏好而供应商有缺货厌恶风险偏好时,供应商的批发价格是其缺货厌恶的减函数,零售商的最优订货量是其浪费厌恶的减函数。
推论表明:当零售商厌恶浪费供应商厌恶缺货时,主导企业供应商为降低因缺货带来的效用损失,提供给零售商的批发价格随其缺货厌恶程度的增强而减小,而零售商的订货策略也随自身浪费厌恶程度的增强而变得保守。
(四)零售商和供应商均有缺货厌恶风险偏好(S-S)
假设β3(β3>0)和λ3(λ3>0)分别是零售商和供应商单位产品的缺货厌恶系数,β3和λ3越大表示相应供应链成员的缺货厌恶程度越高。同时假设Ur3(πr(b))和Us3(πs(b))分别为零售商和供应商有缺货厌恶偏好时的效用函数。此时零售商与供应商的期望效用如下:
E[Ur3(πr(b))]=pS(Q)+bI(Q)-
=(p-b+gr)S(Q)-(w-b)Q-
E[Us3(πs(b))]=wQ+vI(Q)-bI(Q)-
(b+gs-v)S(Q)+(w-c+v-b)Q-μgs-
命题5E[Ur3(πr(b))]是关于Q的凹函数,存在唯一的Qr3使E[Ur3(πr(b))]取得最大值,且
命题6E[Us3(πs(b))]是Q的凹函数,当满足w-c≤b-v时,存在唯一的Qs3使E[Us3(πs(b))]取得最大值,且
同样得到批发价格
推论3 当零售商和供应商均有缺货厌恶风险偏好时,零售商的最优订货量是其缺货偏好的增函数,供应商的批发价格是缺货偏好的减函数。
推论表明:当零售商和供应商都厌恶缺货时,占领导地位的供应商给零售商的批发价格随其缺货厌恶程度的增强而减小,零售商为降低缺货带来的效用损失,其订货策略也更激进。
(五)零售商和供应商均有浪费厌恶风险偏好(W-W)
假设β4(β4>0)和λ4(λ4>0)分别是零售商和供应商单位产品的浪费厌恶系数,β4和λ4越大表示相应供应链成员的浪费厌恶程度越高。假设Ur4(πr(b))和Us4(πs(b))分别为零售商和供应商有浪费厌恶偏好时的效用函数。此时回购契约下零售商与供应商的期望效用如下:
E[Ur4(πr(b))]=pS(Q)+bI(Q)-wQ-
(p-b+gr)S(Q)-(w-b)Q-
E[Us4(πs(b))]=wQ+vI(Q)-bI(Q)-
(b+gs-v)S(Q)+(w-c+v-b)Q-
命题7E[Ur4(πr(b))]是关于Q的凹函数,存在唯一的Qr4使E[Ur4(πr(b))]取得最大值,且
命题8E[Us4(πs(b))]是Q的凹函数,存在唯一的Qs4使E[Us4(πs(b))]取得最大值,且
同样可得
推论4 当零售商和供应商均有浪费厌恶风险偏好时,零售商的最优订货量是其浪费偏好的减函数,供应商的批发价格是其浪费偏好的增函数。
推论表明:当零售商和供应商都厌恶浪费时,占领导地位的供应商给零售商的批发价格随其浪费厌恶程度的增强而增大,零售商为减小浪费带来的效用损失风险,其订货策略也更为保守,结论也与现实情况相一致。
三 数值分析
为了更好地反映零售商和制造商的风险偏好对供应链绩效的影响,同时更加直观地反映不同风险偏好系数下零售商订货策略和供应商定价策略的变化趋势,将本文四种不同风险偏好组合情形下的研究结论进行数值分析。假设零售价格p=20,批发价格w=10,生产成本c=4,残值v=3,回购价格b=8,零售商缺货成本gr=1,供应商缺货成本gs=1,两个成员的风险偏好系数满足βi~[0,5]和λi~[0,5],为方便计算和分析,假定市场需求服从F(x)~[10,50]的均匀分布,利用Mathematica8.0软件得到S-W、W-S、S-S、W-W四种情形下零售商订购策略和供应商定价策略的变化情况,具体如图1-图4所示。

图1 S-W型风险偏好组合下决策者订货策略
由图1可知,当零售商具有缺货厌恶偏好而供应商具有浪费厌恶偏好(S-W型),零售商的最优订购量是其缺货厌恶偏好的增函数,零售商的最优订购量随其缺货厌恶系数增大而增大,供应商给零售商的批发价格也是其浪费厌恶偏好的增函数,供应商给的批发价格也随其浪费厌恶程度的增大而增大。供应商浪费厌恶系数越高,表明供应商越讨厌浪费,不希望零售商订购过多的产品而销售不出去,所以供应商只有通过提高批发价格来降低这种浪费的风险,供应商越厌恶浪费,所提供给零售商的批发价格也越高。同时零售商越厌恶缺货,其缺货厌恶系数也越高,结果零售商为了避免因市场上出现销售产品的缺货而给其带来损失的情况,只有不断加大其销售产品的最优订货量。
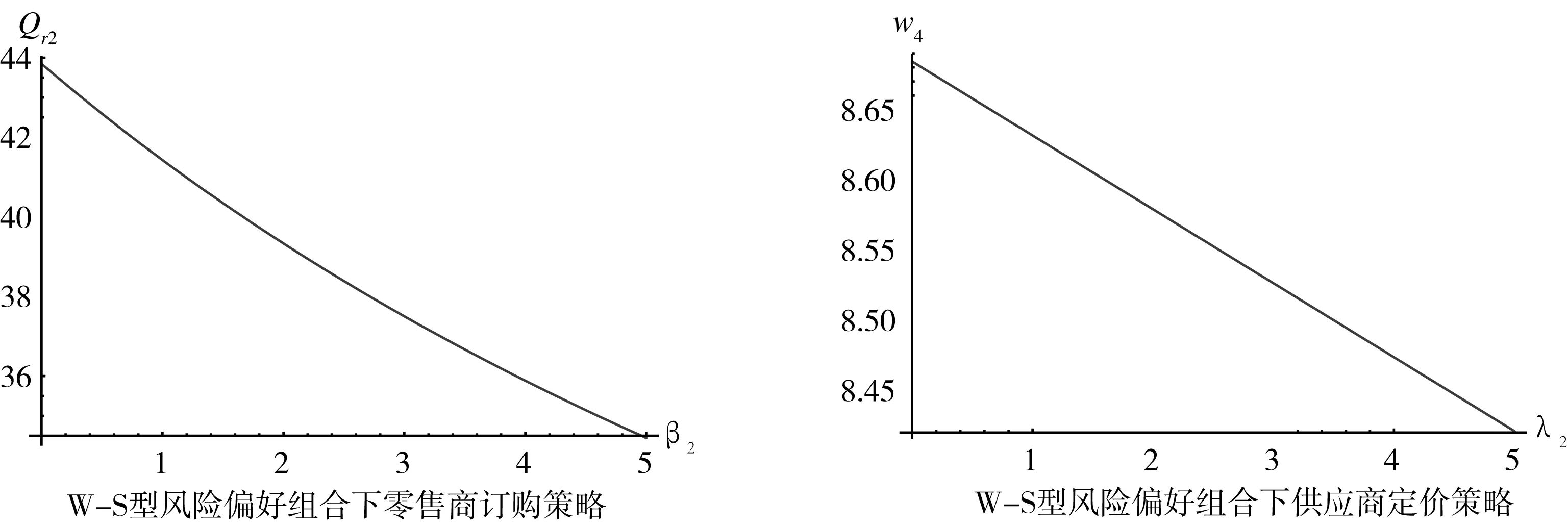
图2 W-S型风险偏好组合下决策者订货策略
由图2可知,当零售商具有浪费厌恶偏好而供应商具有缺货厌恶偏好(W-S型),零售商的最优订购量随其浪费厌恶程度增大而降低,同时供应商的批发价格也随其缺货厌恶系数的增大而减小,供应商通过降低批发价来减少缺货带来的损失,零售商通过减少订购量来降低浪费风险。
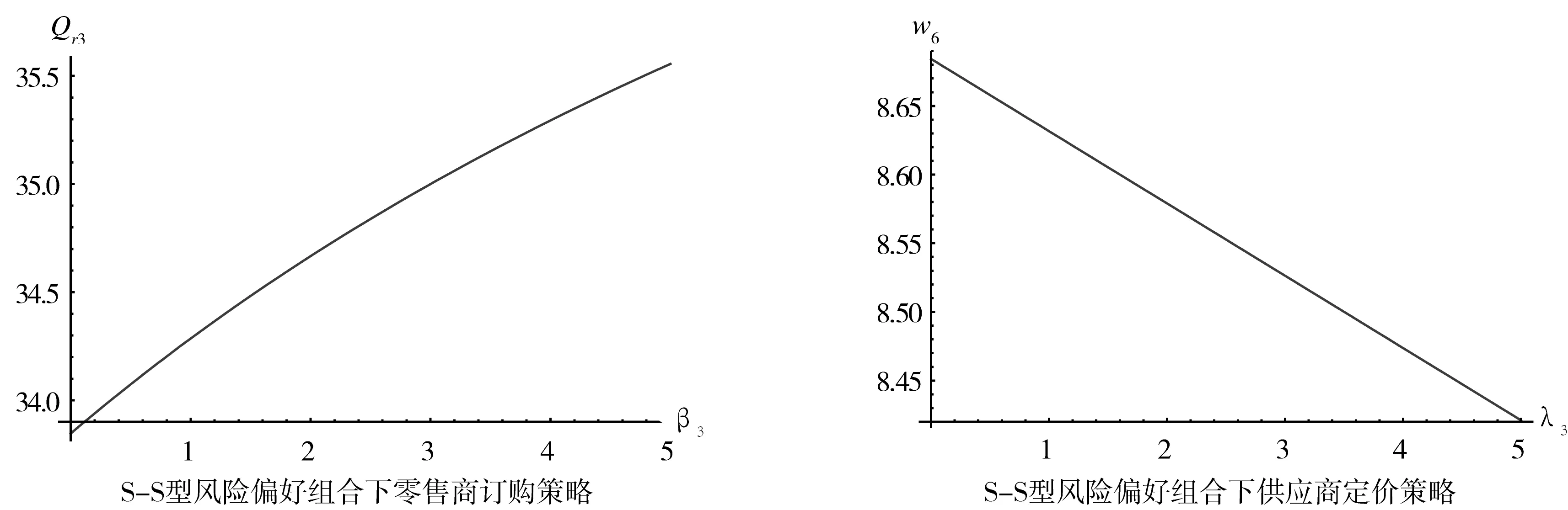
图3 S-S型风险偏好组合下决策者订货策略
由图3可知,当零售商和供应商同时具有缺货厌恶偏好(S-S型),零售商的最优订购量会随其缺货厌恶系数增大而增大,而供应商的批发价格会随其缺货厌恶系数的增大而减小,供应商通过降低批发价格,刺激零售商订购更多的产品,从而减少因缺货带来的损失,而零售商由于厌恶缺货,只能通过增大订购量来避免缺货风险。
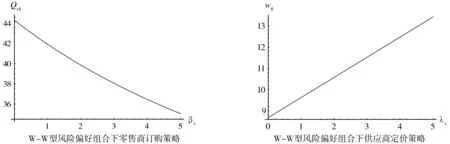
图4 W-W风险偏好组合下决策者订货策略
由图4也可知,当零售商和供应商同时具有浪费厌恶偏好(W-W型),随着浪费厌恶程度的增大,零售商的最优订购量减少,供应商的批发价格增大,零售商通过减少订购量、供应商通过提高批发价格来降低因为浪费带来的损失。
图1和图2所示的模型中,当决策者风险规避程度确定时,供应链系统会通过批发价格这一关键因素调整零售商的订货策略,从而形成一种最优平衡状态,无论对供应链整体还是成员决策者来说,是一种综合风险偏好和期望效用水平后的折中。图3和图4所示的模型中,这样的结果很可能导致供应链库存极高或极低两种偏激现象,此时回购契约发挥了调节作用,即通过回购价格的合理变动调整零售商的订货策略和供应商的定价策略,使其达到某一最优水平,实现供应链绩效的最优化。
四 结论
本研究同时考虑供应商和零售商的缺货厌恶和浪费厌恶两种风险偏好,引入回购契约研究四种不同决策偏好组合下的供应链订货决策模型,分析了成员风险偏好对订货策略、定价策略和协调过程的影响,并通过数值实验进一步量化风险偏好系数、订货量和批发价格间的关系,得出如下结论:
(1)供应商的决策风险偏好对供应链的绩效影响更明显。供应商在供应链系统中占主导地位,拥有更强大的谈判力和领导力,在Stackelberg博弈中充当领导者角色,而作为跟随者的零售商在优化最优订购量时必然充分考虑到供应商的效用最大化这一前提,零售商的风险偏好也仅仅是在这一范围内有所变动。该结论进一步验证了Ohmura[22]和Ohmura等[24]所得的部分结论,即占主导地位的供应商的决策风险偏好对供应链影响更突出。
(2)当零售商有缺货厌恶偏好而供应商有浪费厌恶偏好时,供应商为降低浪费风险,批发价格随其浪费厌恶程度的增大而增大,零售商的最优订购量随其缺货厌恶系数增大而增大,此时零售商会制定激进型订货策略;当零售商有浪费厌恶偏好而供应商有缺货厌恶偏好时,主导企业供应商为降低因缺货带来的效用损失所提供给零售商的批发价格随其缺货厌恶程度的增强而减小,零售商为降低浪费风险也会相应地制定保守型订货策略。上述两个结论也与实际情况相符合,但与庞庆华[10-11]在收益共享契约中单独考虑某一节点缺货或浪费厌恶偏好时所得结论有所不同,其模型是本文的一种特殊情况(即风险偏好系数为零),本模型更为一般化,同时考虑供应商和零售商的风险偏好更加符合实际。
(3)当零售商和供应商均有缺货厌恶风险偏好时,占领导地位的供应商给零售商的批发价格随其缺货厌恶程度的增强而减小,一定程度上会刺激零售商的需求量,使其订货策略相对激进。当零售商和供应商均有浪费厌恶风险偏好时,占领导地位的供应商给零售商的批发价格随其浪费厌恶程度的增强而增大,会导致零售商的需求萎缩,其订货策略也更保守。本文引入回购契约对零售商的订货策略进行了调整,使其订货量满足供应链整体绩效最优化的目的。上述结论弥补了庞庆华[10-11]两种情形下收益共享无法实现协调的不足,其根本原因是未考虑缺货损失成本从而使收益共享系数“浮增”,同时该结论也与现实情况相一致。
本文为四种不同风险偏好组合类型的供应链决策者在订货和定价策略上提供了一定的理论参考,但模型基础为简单的二级供应链,未来可进一步拓展到三级或多个成员构成的供应链网络,并将其应用于实证中充分展开研究。
