高速铁路实测钢轨廓形数据分析与平滑处理方法

2019-03-04，，，

铁道建筑 2019年2期

，，，

(1.中国铁道科学研究院研究生部，北京 100081；2.中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081)

随着我国高速铁路运营里程不断增长，铁路领域内对于获取实测钢轨廓形数据的需求快速增长。实测钢轨廓形数据是钢轨磨耗计算、轮轨接触参数计算以及钢轨廓形分析的基础。虽然大多数测量设备在导出数据时已经作了一定的平滑处理，但由于设备摆放误差、钢轨表面脏污未得到有效清理等原因，实测数据中仍存在畸变点[1]。钢轨廓形平滑处理一般采用样条平滑法、滑动平均法、中值滤波法等方法[1-7]。常用方法不能达到理想的平滑效果，因此需要研发一种高速铁路实测钢轨廓形畸变点平滑处理方法。

本文在分析实测高速铁路钢轨廓形的基础上，结合法向距离曲线计算、FFT及其逆变换和边界延拓方法，提出了一种能够有效消除钢轨廓形畸变点的平滑处理方法。

1 常用钢轨廓形平滑处理方法

图1 实测钢轨廓形及其畸变点局部放大

图2 标准CN60钢轨廓形

实测钢轨廓形如图1(a)所示，图中虚线部分可见较严重畸变点，放大后如图1(b)所示。标准CN60钢轨的轨头大致包括两部分，如图2所示。其中一部分如实线所示，为直线段。另一部分如虚线所示，为曲线段。高速铁路钢轨服役过程中，区段Ⅰ和区段Ⅲ一般情况下不发生磨耗。可利用区段Ⅰ和区段Ⅲ的实测数据，采用旋转、平移等操作将钢轨廓形进行坐标对齐。在廓形对齐的基础上，进行平滑处理。

1.1 样条平滑法

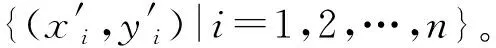
(1)

式中：p为平滑化参数，p∈[0,1]，当p为0时，光滑处理后的图形为最小二乘法拟合的直线，当p为1时，光滑处理后的图形与原图形相同；yi为原始输入数据的y坐标;f(xi)为与yi相对应的xi的三次样条函数在xi点的函数值；λ为粗糙度权重系数；d2f(t)是函数f的二阶导数。

在某些情况下，样条平滑法得到的数据存在“回折”的现象，如图3虚线部分所示。

图3 样条平滑法处理后的钢轨廓形

1.2 滑动平均法

滑动平均法是一种由来已久，较为直观简便易于理解的方法。对于点序列{(xi,yi)|i=1,2,…,n}，依次计算m个点坐标的平均值，替换中间点的数值，从而使数据序列摆脱随机性的干扰。其公式为

(2)

式中：q为正整数；m为滑动平均的范围，或称为窗长，m=2q+1。

滑动平均法适用于消除周期性噪声，然而对于数据中随机发生的脉冲型的畸变点效果较差。采用滑动平均法处理后的钢轨廓形同样存在“回折”现象，如图4 所示。

图4 滑动平均法处理后的钢轨廓形

1.3 中值滤波法

对于点序列{(xi,yi)|i=1,2,…,k,…,m}，第k个点xk所对应的值yk取该点前后n个点的中位数。计算过程分为2种情况:当n为奇数时，yk取yk-(n-1)/2,…,yk+(n-1)/2的中值；当n为偶数时，yk取yk-n/2，…，yk+n/2的中值。

中值滤波方法简单易用，对于消除单点式的干扰有很好的作用，但对于消除钢轨廓形中连续多点的干扰效果不理想。当n≤9时，畸变点不能得到有效消除，如图5所示；当n>9时，曲线的首尾出现向上的折线，如图6所示。

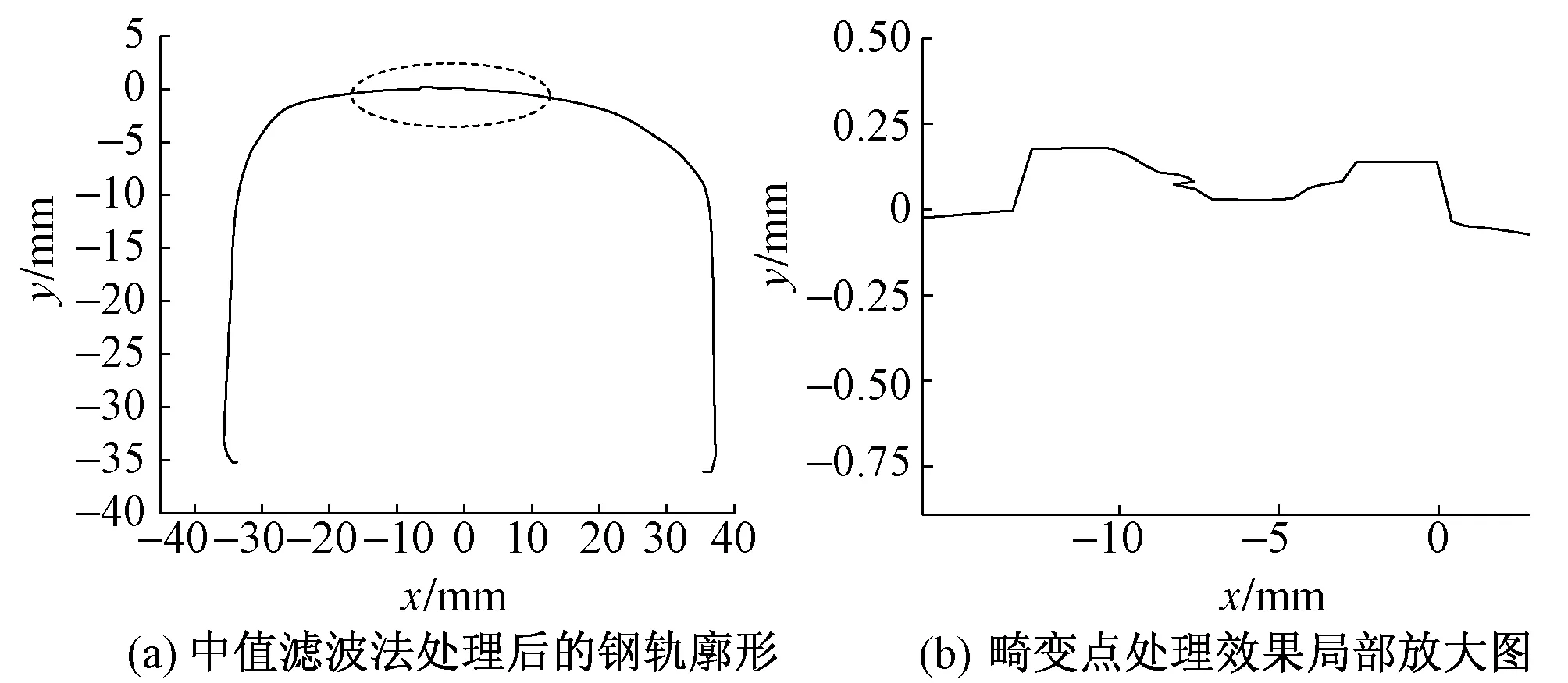
图5 中值滤波法处理后的钢轨廓形(n≤9)

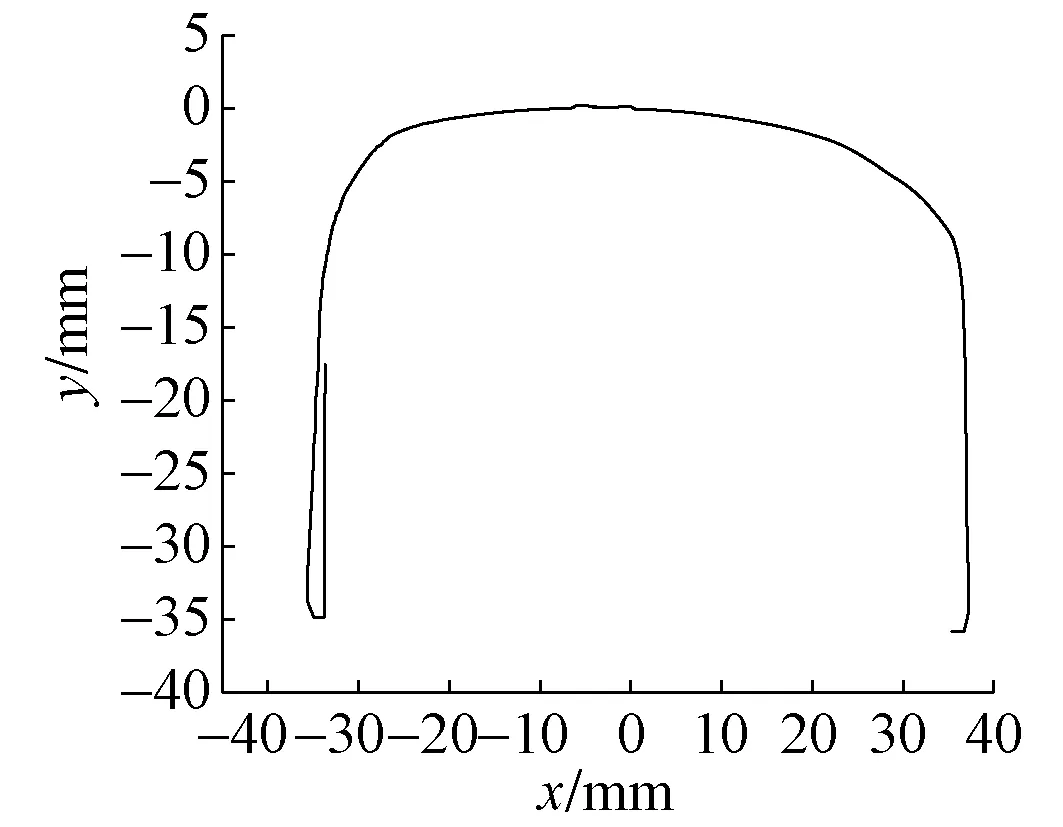
图6 中值滤波法处理后的钢轨廓形(n>9，n=12)

综上所述，常用平滑方法处理效果不理想，需要研究一种适用于实测钢轨廓形畸变点的平滑处理方法。

2 法向距离曲线滤波法

2.1 计算流程

针对高速铁路实测钢轨廓形的特点，提出了法向距离曲线滤波法：首先，将实测廓形与标准廓形对齐，计算实测钢轨廓形与标准廓形的法向距离；其次，结合FFT、逆FFT和边界延拓方法，对法向距离曲线进行滤波；最后，将滤波后的法向距离曲线叠加到标准廓形上，得到平滑处理后的实测钢轨廓形。计算流程如图7所示。

图7 计算流程

2.2 法向距离曲线计算

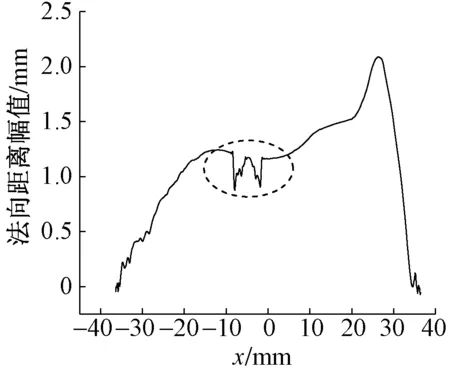
图8 实测钢轨廓形与标准钢轨廓形法向距离曲线

2.3 FFT及其逆变换

通过对法向距离曲线作傅里叶变换可以看出，误差项的能量主要集中在波数相对大的波段上。利用傅里叶变换和逆傅里叶变换构造一个低通滤波器[9]，自动滤除钢轨廓形中的高频畸变部分。

记法向距离曲线上的采样点为x(i),i=0,1,2,…,N-1，其中N表示采样点数，采样间隔为9个点/mm。对法向距离进行离散傅里叶变换得到X(k)和它所对应的波数f(k),即

假定小于3 mm波长的成分为畸变点。找出波数f(k)大于1/3的最大整数K，得

K=(N-1)/9×(1/3)+1

(4)

式中：[]表示向下取整运算符。

令X(K),X(K+1),…,X(N-1)傅里叶系数为0。对X(0),X(1),X(2),…,X(N-1)按式(5)进行逆傅里叶变换得到滤除趋势项后的法向距离曲线。

滤波后的法向距离曲线如图9所示。

图9 滤波前后的法向距离曲线对比

2.4 边界延拓

由图9可知，滤波后的法向距离曲线很好地消除了局部畸变点的影响，使得曲线光滑。事实上，采用FFT方法进行低通滤波过程中，会产生如图9虚线框部分所示的边界效应[10-11]，使滤波后的曲线偏离法向距离曲线。为了消除这种影响，本文采用了镜像延拓方法[12]。

记信号x(t)在时刻序列t={ti,i=1,2,…，lx}上的采样值为x={xi,i=1,2,…，lx}，其中xi=x(ti)，lx为待延拓的信号长度。另外，记采样时刻段的极大值点序列为Pmax={Pmax,j,j=1,2,…，m0}，采样时刻段的极小值点序列为Pmin={Pmin,j,j=1,2,…，n0}。

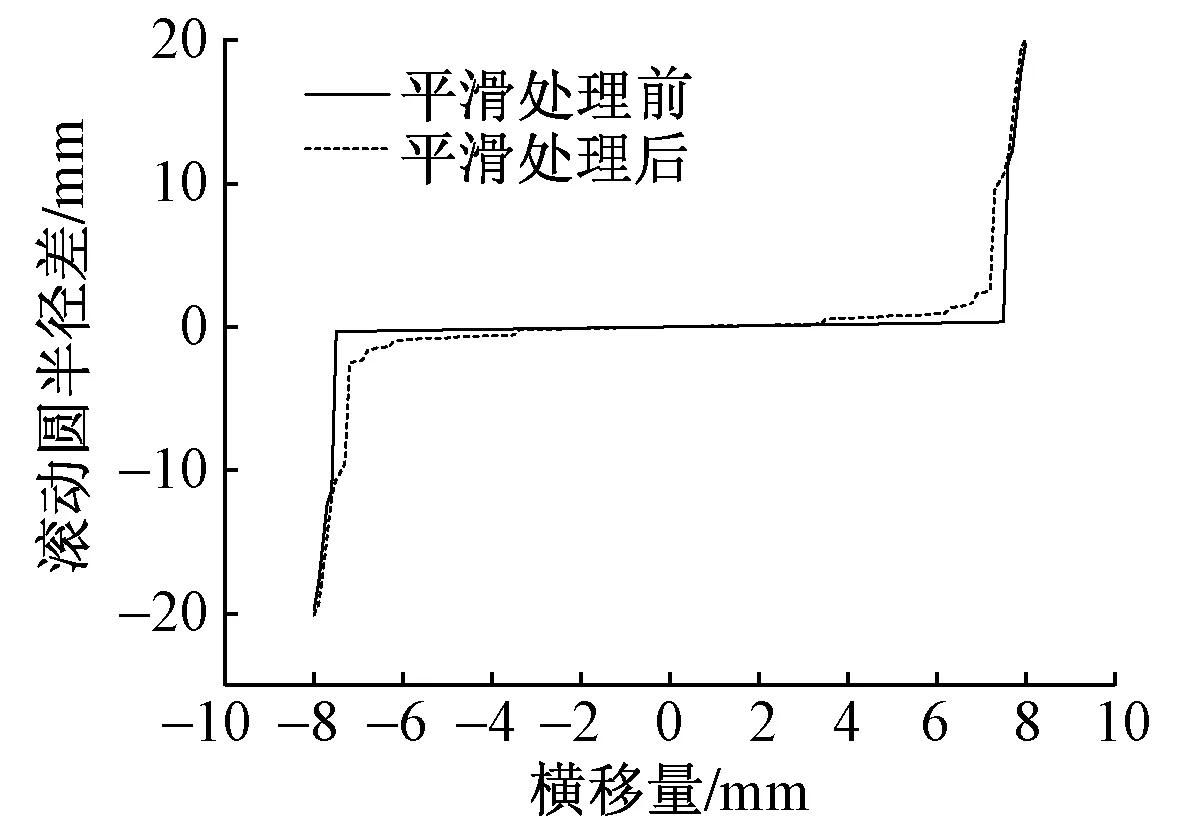
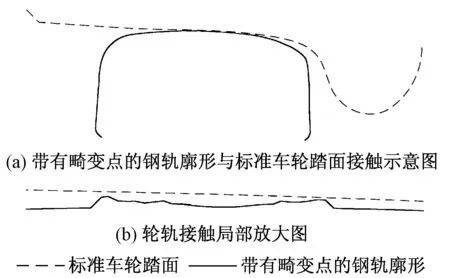
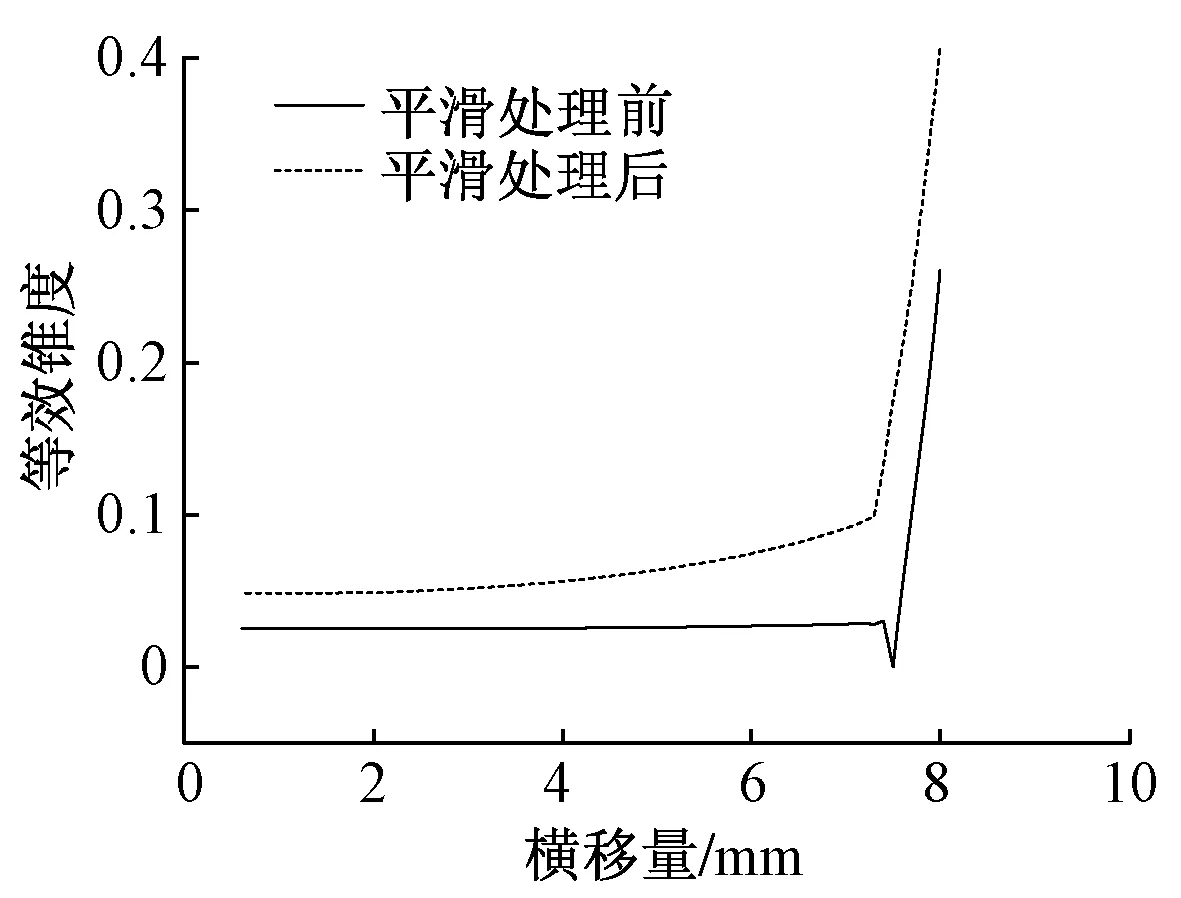
如果Pmax,m0

如果Pmax,m0>Pmin,n0则根据Pmin,n0和tlx的大小关系确定镜像映射轴。若Pmin,n0≥tlx则镜像映射轴取为τ=tlx；若Pmin,n0

经过边界延拓再进行滤波的法向距离曲线如图10 所示。可知经过边界延拓再滤波的法向距离曲线受边界效应的影响明显减小。将经过边界延拓和滤波后的法向间距曲线叠加到标准型面上，得到重构的实测钢轨廓形曲线，如图11所示。从图中可看出，重构的实测廓形消除了畸变点。

图10 边界延拓和滤波后的法向距离曲线

图11 平滑处理后的实测钢轨廓形与原始钢轨廓形对比

3 处理效果分析

将实测钢轨廓形进行平滑处理，利用处理后的钢轨廓形进行轮轨接触参数计算[13-14]，以接触位置、滚动圆半径差(RRD)曲线以及等效锥度为例来说明处理效果。

3.1 轮轨接触位置对比

通过多体动力学软件SIMPACK计算钢轨廓形处理前后的轮轨接触点位置，计算结果如图12所示。可知，平滑处理前的钢轨廓形接触点较为集中，尤其在发生轮缘接触前，接触点集中在畸变点范围内。反之，平滑处理后的钢轨廓形轮轨接触点分布相对均匀，说明轮轨接触点发生转移时较为连续，未受到畸变点的影响。综上可知，实测钢轨廓形平滑处理效果显著，按照处理后的钢轨廓形计算得到的轮轨接触参数更加真实可靠。

图12 平滑处理前后的轮轨接触点计算结果

3.2 滚动圆半径差曲线计算结果对比

利用规范UIC519编制程序,计算轮轨接触左右滚动圆半径差曲线。按照平滑处理前的钢轨廓形计算得到的滚动圆半径差曲线如图13实线所示。横移量±7.5 mm范围内的滚动圆半径差曲线接近一条直线，表明左右滚动圆半径差几乎未发生变化。其原因是：如图14所示，轮轨接触点始终在车轮与钢轨畸变点上，因此左右滚动圆半径差几乎未改变。