深海平台操舵机构运动精度可靠性分析

，，

(中国船舶科学研究中心 深海载人装备国家重点实验室，江苏 无锡 214082)

新型海洋装备深海平台[1]的操舵机构的运动精度设计参考的资料有限，使得运动精度可靠性分析、精度校核以及改进设计都存在困难。进行深海平台操舵机构运动精度可靠性分析，需要将构件加工尺寸、角度等参数考虑成随机变量[2]，建立操舵机构运动到位的功能函数，根据功能函数的特点选择一次二阶矩法或者蒙特卡罗法进行求解。对操舵机构运动精度进行参数灵敏度分析[3-4]，计算各影响参数的灵敏度因子[5]，以获得各参数的微小变化对运动精度的影响程度，为提高运动精度提供改进依据。

本文以某深海平台摆缸式操舵机构为对象，开展操舵机构运动精度可靠性分析，将机构尺寸、装配误差考虑成随机变量，建立摆缸式操舵机构运动精度可靠性模型；分析运动精度与舵叶偏角之间的规律，为精度校核角度的选取提供依据；通过灵敏度分析获得各影响因素对操舵机构运动精度失效的影响程度排序，作为提高操舵机构运动精度可靠性改进设计的依据。

1 机构组成及工作原理

图1 某深海平台端铰摆缸式操舵机构组成

某深海平台采用端铰摆缸式操舵机构组成见图1。摆缸式操舵机构的主要优点是重量轻，布置灵活。但转矩特性不够理想，其转舵力矩随着舵角的增大而减小[6]。工艺上对油缸和活塞加工精度及密封要求均较高。由于深海平台系统众多、空间相对较小，且要携带大量作业装备，因此选用布置灵活的摆缸式操舵机构。

摆缸式操舵机构的工作原理为舵叶需要上偏时，通过液压系统控制油缸活塞杆伸长，推动舵柄旋转，舵柄带动舵叶绕舵杆上偏，油缸伸长的同时会绕基座销轴旋转。下偏时只需通过液压系统控制油缸活塞杆收缩。

对摆缸式操舵机构进行简化见图2。BC为活塞式油缸，AC为舵柄，B点为油缸转轴，A点为舵柄转轴，即舵杆。BCA为舵叶未偏转状态，BC1A为舵叶上偏状态，BC2A为舵叶下偏状态。

图2 摆缸式操舵机构简化示意

2 机构运动精度可靠性分析

2.1 摆缸式操舵机构运动精度可靠性建模

研究摆缸式操舵机构的运动精度可靠性，即是研究舵叶是否偏转到位的可能性大小，具体可根据舵柄偏转的角度是否精确来计算该摆缸式操舵机构的运动精度可靠性的大小。

以舵叶上偏为例进行运动精度可靠性分析。

舵叶上偏时，机构运动分析见图3。

图3 摆缸式操舵机构运动分析

(1)

实际工作时，当油缸伸长到L3时，舵叶实际偏转角θ4与各输入量存在以下关系。

(2)

根据深海平台舵装置设计要求，当实际偏转角与要求偏转角之差的绝对值大于给定值时，即认为操舵机构运动精度不满足要求。

记舵偏角允许偏差为θ0，则操舵机构运动到位的功能函数为

(3)

操舵机构运动精度满足要求时，θ<0；不满足要求时，θ>0。

则操舵机构运动精度失效概率为

(4)

2.2 摆缸式操舵机构运动精度可靠性计算

由于设计、制造和装配过程中诸多因素的影响，操舵机构中各零件加工尺寸、装配角度等不可避免的存在着偏差，在进行机构运动精度可靠性分析时，应将各零件尺寸、角度等参数考虑成随机变量，据统计分析，均服从正态分布[4]。同时，由于各零件是独立加工、安装的，这些随机变量间是相互独立的。

从式(2)可以看出，θ4与尺寸长度L1、L2、L3和角度θ1、θ2有关，而尺寸长度L1、L2、L3和角度θ1、θ2均为随机变量，故θ4也应为随机变量，服从正态分布，用蒙特卡罗法计算得到。

(5)

由式(5)可见，操舵机构运动精度失效状态函数由2个线性表达式组成，可用一次二阶矩法求解其失效概率，即可靠性系数

(6)

由此可得操舵机构运动精度失效概率为

Pf=Φ(-β1)+Φ(-β2)

(7)

2.3 算例

某深海平台摆缸式操舵机构尺寸、角度参数值及标准差见表1。

表1 某深海平台摆缸式操舵机构尺寸、角度参数值

机构尺寸、角度公差选自GB/T1804—2000[7]，公差等级为中等m。液压油缸工作行程公差±3 mm。设计偏角30°，允许偏差为1°。

舵叶实际偏转角θ4的表达式如式(3)，通过蒙特卡罗法可以获得θ4的均值和标准差，即

σθ4=0.24°

可靠性系数为

故舵偏角为30°时，操舵机构运动精度失效概率为Pf=Φ(-β1)+Φ(-β2)=3.142×10-5。

3 机构运动精度与舵偏角的关系

依次对舵叶上偏角为0°、5°、10°、15°、20°、25°和30°进行舵偏角误差分析。各偏角对应的油缸设计长度及标准差见表2。

表2 不同舵偏角对应的油缸设计长度及标准差

将表1和表2的参数值代入式(3)，通过蒙特卡罗法求得各设计舵偏角下的舵叶实际上偏角θ4的均值和标准差，见表3。

表3各设计舵偏角下的舵叶实际上偏角
θ4的均值和标准差(°)

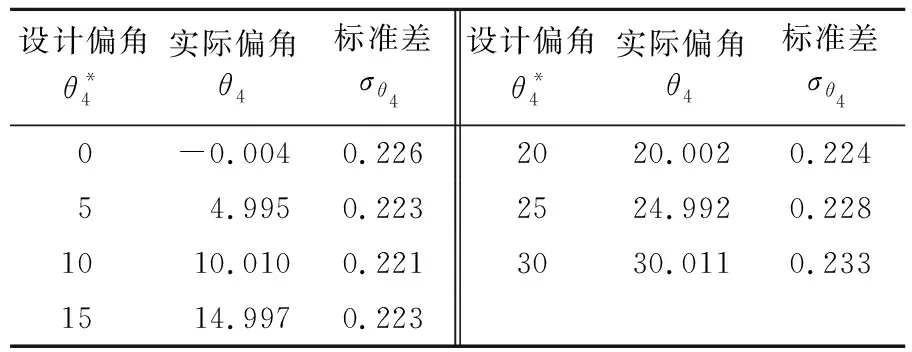
设计偏角θ*4实际偏角θ4标准差σθ4设计偏角θ*4实际偏角θ4标准差σθ40-0.0040.2262020.0020.22454.9950.2232524.9920.2281010.0100.2213030.0110.2331514.9970.223

可以看出，舵叶偏角在工作范围0～30°以内，舵叶实际偏角的标准差随舵叶偏角的变化很小，标准差均在0.22°～0.24°范围内，即最大误差不超过0.72°。为了更明显地呈现变化趋势，增加40°、50°偏角误差分析，见表4。

表4舵偏角40°和50°误差分析(°)

设计偏角θ*4油缸长度L3标准差σL3实际偏角θ4标准差σθ4401 310.1140.0010.247501 354.4150.0100.270

绘制舵叶上偏0°～50°范围内，舵偏角标准差随舵偏角的变化曲线，见图4。

图4 舵偏角标准差随舵偏角的变化

由图4可见，舵偏角标准差随着舵偏角的增大先小幅降低，在舵偏角为10°附近取得最小值，后随着舵偏角的增大而逐步增大，在舵偏角取的最大值时，舵偏角标准差也最大。

进一步分析发现，舵偏角为10°时，舵柄和油缸所在直线组成的夹角AC1B为90.52°，舵柄与油缸基本垂直。故总结出摆缸式操舵机构运动误差变化规律如下：当舵柄与油缸呈90°时，舵偏角标准差(误差)最小；舵柄与油缸夹角与90°相差越大，舵偏角标准差(误差)越大。

针对摆缸式操舵机构，舵偏角最大往往代表着舵柄与油缸夹角与90°差值最大，因此对于舵叶偏转全角度范围内设计精度要求不变的情况，进行舵偏角运动精度分析时，选择最大舵偏角进行误差校核通常是可以满足分析要求的；但对于舵偏角不同实行设计精度分级的情况，应在每一级别精度要求的偏角范围内，选择舵柄与油缸夹角与90°差值最大的偏角进行精度验证。

4 机构运动精度可靠性灵敏度分析

摆缸式操舵机构各零件在加工、装配过程中造成的尺寸、角度等偏差都会导致舵叶偏转角度的误差，如果对所有影响参数进行误差控制则会在舵叶偏角误差减小的同时带来巨大的经济负担。对影响操舵机构运动精度的各因素进行灵敏度分析，重点控制对操舵机构运动精度灵敏度较高的参数误差，可以在经济代价较小的情况下有效提高操舵机构运动精度。

常用的灵敏度因子有设计点处的灵敏度因子和均值灵敏度因子。均值灵敏度因子近似地反映了影响因素在均值处发生了微小扰动时系统失效的变化情况，代表实际工程结构中，该因素对结构失效的影响程度。本文选用均值灵敏度因子。

灵敏度因子计算公式[8]如下。

(8)

式中：G(x1,x2,…,xn)为失效状态函数；P为均值点。

操舵机构运动精度失效状态函数为

(9)

将表1中的参数代入式(11)和式(12)，计算得到各影响因素的灵敏度因子，见表5。

表5 操舵机构运动精度失效参数灵敏度因子

由表5可见，影响操舵机构运动精度失效的灵敏度因子从大到小依次为L3、L1、θ1、θ2、L2，该排序说明这些因素对操舵机构运动精度失效的影响程度大小。其中，油缸长度L3所占百分比最大，达到48.95%，因此在设计、制造过程中，应首先严格控制油缸的运动误差。其次是L1、θ1和θ2，在工艺和经济允许的情况下，叶应加强这3个参数的质量控制，提高公差精度等级。而舵柄长度L2对失效影响的百分比仅占2.6%，提高其公差精度效果不明显，可以暂不提高其公差精度。

因没有考虑磨损对操舵机构运动精度的影响，故所分析应为操舵机构寿命初期的运动精度可靠性，后续可以进行销轴磨损导致的运动精度退化特性和可靠性寿命分析。