豪华邮轮主尺度要素统计分析
2019-03-04,,
,,
(大连理工大学 a.船舶CAD中心; b.工程装备结构分析国家重点实验室,辽宁 大连 116024)
豪华邮轮是一种高技术、高附加值、高可靠性,以及高要求的船舶,对豪华邮轮进行的研究多集中于豪华邮轮的安全性问题[1-2]以及豪华邮轮的发展近况和趋势[3-4],也有部分学者对豪华邮轮的关键参数进行了研究[5-6],但是,少见对豪华邮轮的设计建造等方面进行深入研究的报道。
船舶设计初期要确定主尺度要素,主尺度选择是否合适直接影响后续设计工作,因此选择恰当的主尺度尤为重要。已有学者对散货船、油船、化学品船、起重船、海监船和渔政船等船型的主尺度做了分析和研究[7-8],但是对豪华邮轮的主尺度还未见研究报道。豪华邮轮主尺度要素的确定还没有明确的经验公式或统计公式。为此,搜集188艘豪华邮轮的船型资料,进行统计分析和敏感性分析,运用回归分析以及神经网络算法总结拟合程度较好的各主尺度要素的回归公式。
1 设计特点
一艘新船的设计不仅要考虑其浮性、稳性、耐波性、快速性等性能,还要考虑实际的航道、码头港口等情况。船舶性能的实现都与主尺度要素有着密切关系,因此,统计分析豪华邮轮主尺度要素,研究主尺度要素与船舶各性能之间的关系是相当重要的。
随着豪华邮轮的大型化,其上层建筑的层数会相应地增加,船舶受风面积就会增大,将对完整稳性产生影响,在设计时应充分考虑船舶的完整稳性和破舱稳性。在安全性方面,豪华邮轮还要特别关注消防、撤离和安全返港等问题。为使乘客获得最大的舒适度,空间的合理分配尤为重要,对振动和噪声也有严格要求。豪华邮轮作为“海上移动城市”,都是沿岸行驶,对环境有一定影响,因此,对废气、污水的排放有着严格的要求。
2 豪华邮轮主尺度回归分析
2.1 统计数据分析
从船级社官网查阅资料,获取了188艘豪华邮轮样本,去除主尺度信息不全以及主尺度相同的样本船,选取船型和经济性较好的139艘豪华邮轮并对其进行主尺度要素的分析。样本中,船长在150~360 m范围内;型宽分布在20~40 m;吃水分布在6.0 ~ 9.5 m;总吨位多数分布在10 000 t ~ 200 000 t,样本船总吨位分布见图1。
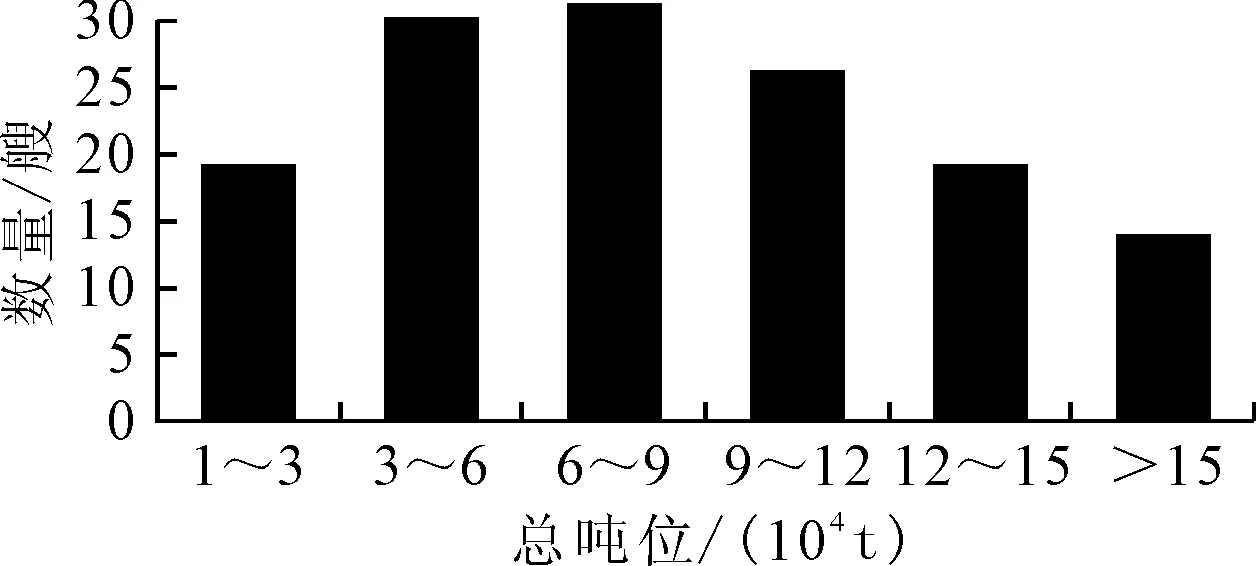
图1 样本船总吨位分布
分析样本可发现,豪华邮轮的吃水随总吨位的变化不大,维持在6.0~9.3 m之内。在设计过程中,应考虑船体材料的使用,控制吃水,这是决定邮轮是否能在特定港口停泊的重要指标。甲板层数随着吨位的增加而增加,服务航速在20~22 kn范围内。乘客、船员人数比值在1.29~3.87范围内,乘客船员比人数是评价邮轮休闲体验设计指数的因素之一,该比值越低邮轮的星级等级越高[9]。豪华邮轮的船长型宽比、船长型深比和船长吃水比都较大,表1为统计样本船的船长Lpp、型宽B、型深D和吃水d的比值范围。当已知某个主尺度时,可根据该比值范围对其他主尺度进行粗估。

表1 样本船主尺度比值范围
2.2 主尺度数学模型的建立步骤
运用统计学方法分析比较样本数据,剔除明显不合理的数据;画出各变量的散点图,根据散点图的趋势,确定数学模型表达形式;再基于最小二乘法,进行回归分析。为使回归公式有较高的可信度,首先对变量进行正态评估,表2为统计数据的偏度和峰度。
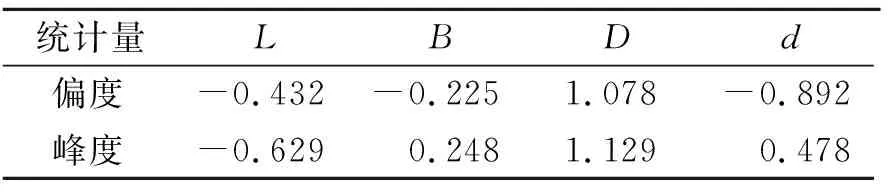
表2 统计数据的偏度及峰度
偏度是反映变量分布形状的一个无量纲数值,它度量了分布的偏斜程度及偏向。正态分布的偏度为0,若偏度大于0,则称分布是右偏;若偏度小于0,则为左偏。峰度是另一个反映变量分布形状的无量纲数值,它表示分布艉部的厚度。以正态分布为标准,若峰度值大于0,则变量分布的艉部比正态分布的艉部粗;若峰度值小于0,则变量分布的艉部比正态分布的艉部细[10]。
由表2可见,各统计量的偏度和峰度都在一定范围内,认为统计数据近似服从正态分布。
2.3 敏感性分析
样本船总吨位数据齐全,为探究主尺度对总吨位影响的重要程度,对他们进行敏感性分析。选择“Explorer of the Seas”号豪华邮船作为参考船型。该船的主尺度:垂线间长274.7 m,型宽38.6 m,型深11.7 m,吃水8.3 m,总吨位138 194 t。船长对总吨位的敏感度分析见图2,横坐标ΔGT/GT0表示样本船与参考船总吨位的差值ΔGT与参考值GT0的比值,纵坐标ΔL/L0表示样本船与参考船船长的差值ΔL与参考值L0的比值。根据同样的方法得到型宽、型深及吃水对总吨位的敏感度,见图2。
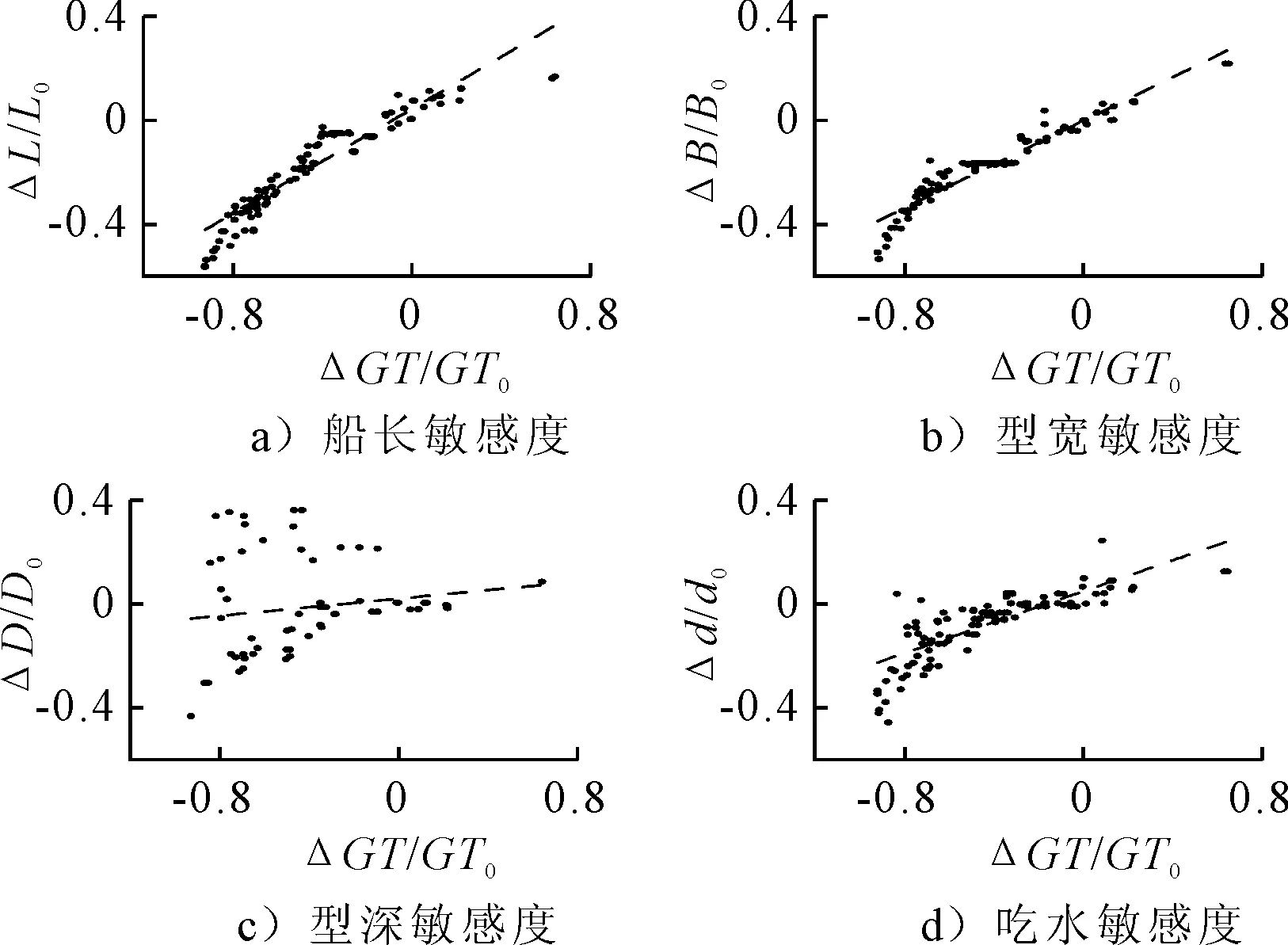
图2 主尺度对总吨位的敏感度
可以看出,船长和型宽对总吨位的敏感度最为明显,而型深和吃水对总吨位的敏感度不明显。各主尺度对总吨位的敏感度系数见图3。
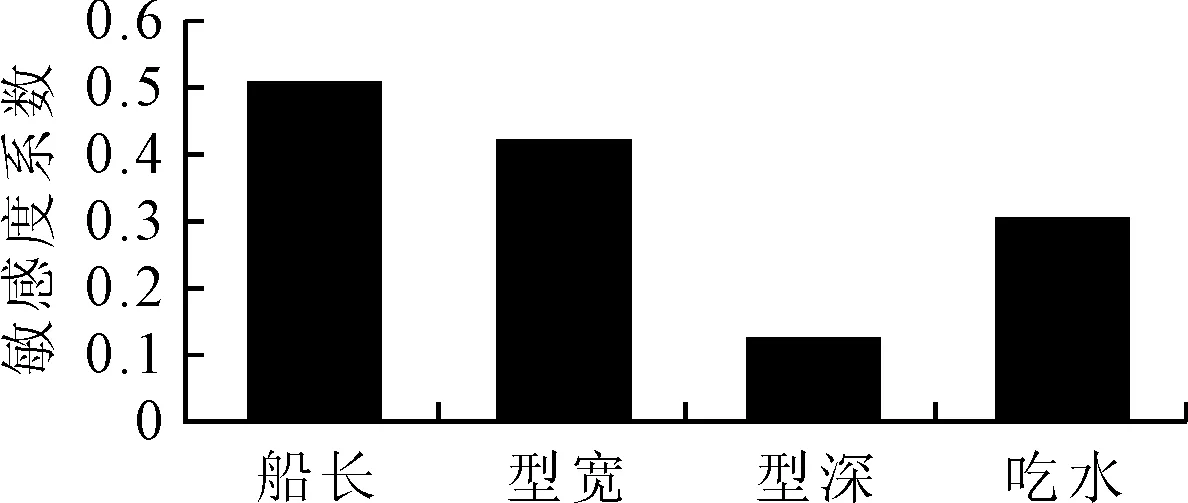
图3 主尺度对总吨位的敏感性系数
2.4 单变量回归分析
根据2.3的敏感性分析可知,各主尺度与总吨位之间都有一定的关系,以总吨位GT为自变量,分别建立各主尺度与总吨位之间的函数关系,各参数回归结果如下。
1)LPP与GT的回归公式。
Lpp=3.684GT0.369
(1)
Lpp=80.604 lnGT-664.81
(2)
R2是衡量回归方程整体拟合度的一个无量纲系数,其值等于回归平方和在总平方和中所占的比率。R2的值越接近1,说明回归函数对样本的拟合程度越好;反之,R2的值越小,说明拟合效果越差。这里认为R2大于0.90时拟合程度较好,其值在0.80~0.90之间表示拟合度一般。式(1)和式(2)的R2值分别为0.95和0.94,说明船长与总吨位的拟合效果较好,式(1)的拟合度优于式(2),拟合曲线见图 4。
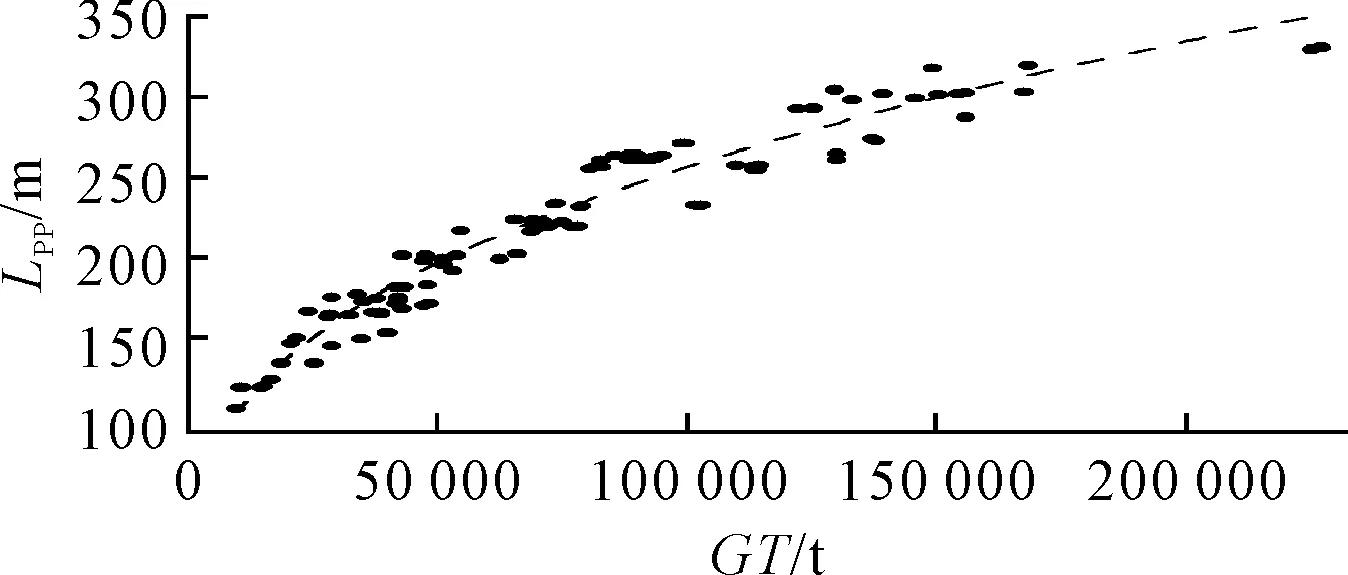
图4 船长与总吨位关系
2)B与GT的回归公式。
B=1.465GT0.576
(3)
B=8.186lnGT-58.922
(4)
式(3)和式(4)的R2值分别为0.95和0.93,型宽与总吨位的拟合度较好,拟合曲线见图5。

图5 型宽与总吨位关系
3)D与GT的回归公式。
D=1.314GT0.184
(5)
D=1.831lnGT-10.123
(6)
式(5)和式(6)的R2值分别为0.83和0.84,型深与总吨位的拟合度一般,拟合曲线见图6。

图6 型深与总吨位的关系
4)d与GT的回归公式。
d=-1.71×10-10GT2+4.941×10-5GT+5.101
(7)
d=1.361 6lnGT-7.471
(8)
式(7)和式(8)的R2值分别为0.80和0.82,吃水与总吨位的拟合度一般,其拟合曲线见图 7。

图7 吃水与总吨位的关系
根据以上的回归分析初步得到各主尺度关于总吨位的回归公式。由各公式中的回归拟合度可以看出,船长、型宽与总吨位的相关性较强,而型深和吃水则与总吨位的相关性较弱。
2.5 多元回归分析
考虑到各主尺度要素受到多重因素的影响,用多元回归分析法对这些主尺度要素进行分析。典型的多元线性回归模型一般形式为
y=β0+β1x1+β2x2+,…,+βnxn+ε
(9)
式中:y为因变量;x1,x2,,…,xn为自变量;β0为常数;β1,β2,,…,βn为回归系数;ε为随机误差。以总吨位为因变量,船长、型宽和吃水为自变量建立回归模型,得到的回归公式如下。
GT=-133 854+371LPP+
5 390.55B-5 505.56d
(10)
lnGT=7.543+0.005LPP+
0.057B+0.071d
(11)
式(10)和式(11)的R2值分别为0.94和0.96,多元回归的拟合度较好。
2.6 BP神经网络模型
在实际应用中,通常选用三层网络结构[11],即输入层、隐含层和输出层。
利用MATLAB中的BP神经网络工具箱对豪华邮轮的主尺度进行分析。将船长、型宽、吃水作为输入层,总吨位作为目标输出对样本进行训练和预测。首先对原始数据进行归一化处理,利用train函数对网络进行训练,用sim函数对训练后的网络进行仿真,最后对结果进行反归一化处理。BP神经网络训练图见图8,BP神经网络预测图见图9。

图8 BP神经网络训练图
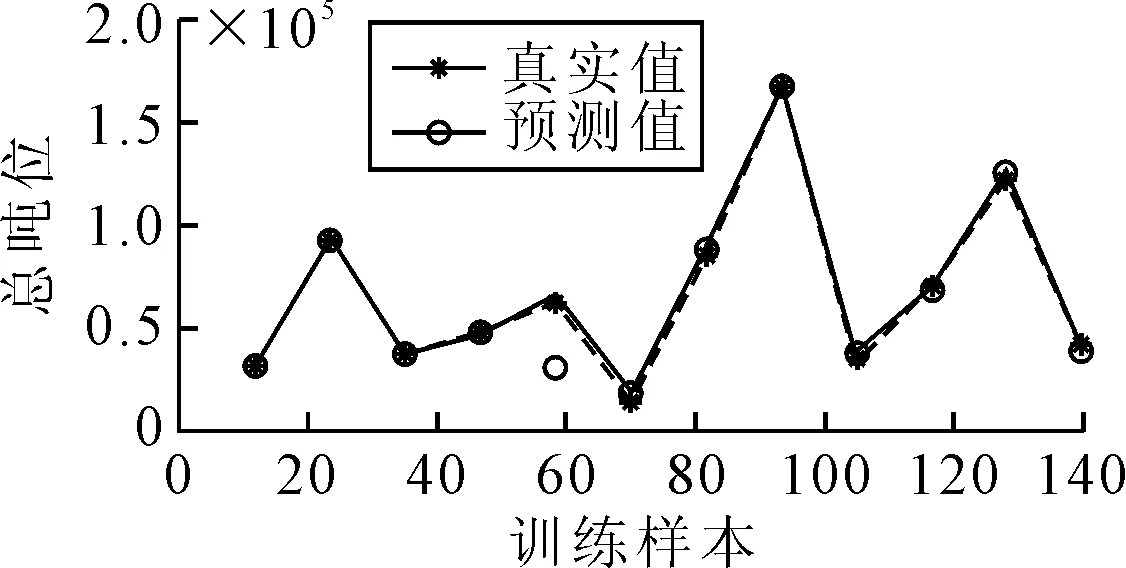
图9 BP神经网络预测图
由图8可见,BP神经网络的训练过程表现良好。图9中,选取的12个测试样本的测试值与真实值的偏差在±5%范围内。该神经网络模型可用于主尺度的预测,设计者根据实际情况对该模型进行变换,在训练模型中输入统计样本的输入数据和输出数据,训练完成后在测试模型中输入已知参数即可得到所需求的参数。
3 回归模型验证
选取5艘未进行回归分析的豪华邮轮进行误差分析,这5艘船舶具体资料见表3。
选用回归分析中拟合度较高的公式以及BP神经网络模型对这5艘船的主尺度进行计算和预测,并与实际值相比较,见表4。
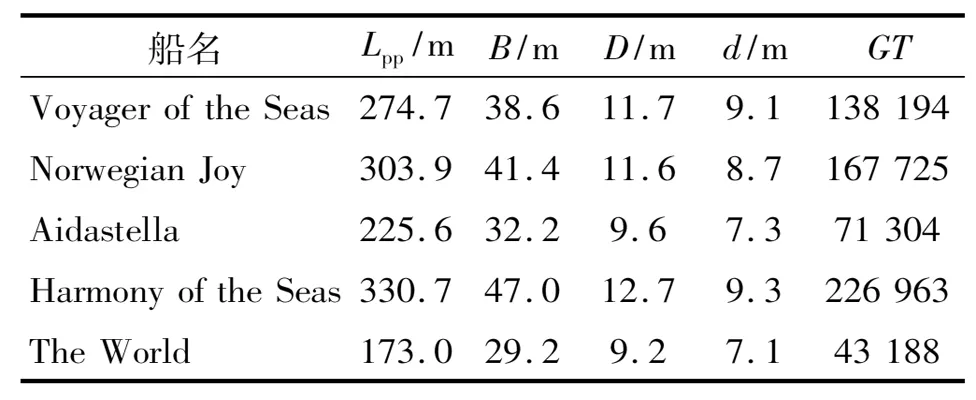
表3 船舶主尺度

表4 回归模型结果验证
从表4中的误差值可以看出,回归模型的误差在±10%范围内,说明回归模型有一定的可信性,可为设计者提供参考;由BP神经网络预测的结果要优于多元回归模型的计算值。
4 结论
回归模型以及BP神经网络模型预测结果较好,适用于船长在150~360 m范围内,型宽在20~40 m范围内,吃水在6 ~ 9.5 m范围内的豪华邮轮的主尺度的预测,为初步设计提供参考。
计算结果还存在一定的误差,在实际设计过程中应根据具体的船型进行适当修正。根据5艘船型的验证结果,应用回归分析和BP神经网络研究豪华邮轮主尺度要素之间的关系是可行的。
