格构增强泡沫夹芯复合材料单向板弯曲疲劳研究
2019-03-02杨方宇
杨方宇, 吴 琦, 何 涛, 王 璐
(南京工业大学 土木工程学院, 江苏 南京 211816)
复合材料不同于金属等其它材料,它具有耐腐蚀、比强度高、比刚度高、质量轻等优点,可广泛应用于制造各种夹芯构件,使得建筑、车辆、舰船、飞机、桥梁等的性能和使用效果得到极大的提高。自从20世纪70年代以来,复合材料在航空航天、交通运输、能源开发等工程和部门日益得到广泛应用[1~3]。
传统的复合材料夹芯结构芯材模量与强度较小,使得夹芯板的刚度和强度偏低。同时由于面板与芯材是由胶粘接而成,芯材与面板之间的抗剥离能力偏弱。本文中的格构增强型复合材料夹层结构,通过在芯材中间增添纤维布腹板,大幅度增强了夹层结构的芯材剪切与平压性能,格构腹板对泡沫芯材起到了增强作用,能有效抑制泡沫剪切裂纹的扩展。格构增强型复合材料夹层结构受弯时,其腹板可有效抑制面板与芯材的剥离破坏,极限承载力与抗弯刚度均高于传统复合材料夹层结构[4]。
国内外学者已对复合材料夹层结构的疲劳性能进行了一定的研究。Shenoi等[5~7]认为,疲劳破坏是夹层结构的主要失效形式之一,复合材料夹层结构的疲劳破坏形式和损伤过程与金属相比尤为复杂,一般认为复合材料夹层梁疲劳破坏主要是由于芯材的剪切破坏所致,所有失效都是由一个起始于芯材的主剪切裂缝造成,其裂纹扩展分为明显的3段过程,而材料剪切模量与复合面板抗弯能力则是夹层结构抗弯水平的核心。Morcous等[8]在其对复合材料夹层板的研究中指出,其采用的蜂窝腹板夹层结构在低载荷比(载荷比R=0.03)的情况下疲劳寿命可达150万次; Mathieson等[9]在其研究的无腹板夹层结构中指出,当将荷载等级控制在0.3(此时R=1)和0.45(此时R=0)时,构件的疲劳寿命次数将可超过200万次以上,这对于结构来说是一个可接受的疲劳性能。
本研究采用MTS试验系统,对该新型夹层结构进行了静力与弯曲疲劳研究,并应用Weibull概率分布模型与累积损伤模型分别对此种夹层结构的疲劳寿命进行分析与预测,为复合材料夹层构件的疲劳设计及计算提供研究依据。
1 试件制备
1.1 试件尺寸
本试验共测试17个试件,其中2个用于静力试验,15个用于弯曲疲劳试验。试件按照ASTM-C393标准进行设计(图1所示),所有试件的尺寸均相同(长度L=350 mm,宽度b=60 mm,高度d=30 mm)。试件的GFRP(Glass-Fiber Reinforced Plastic,玻璃纤维增强塑料) 面层厚度ts为2.5 mm,试件腹板厚度为1.2 mm,腹板间距为50 mm。
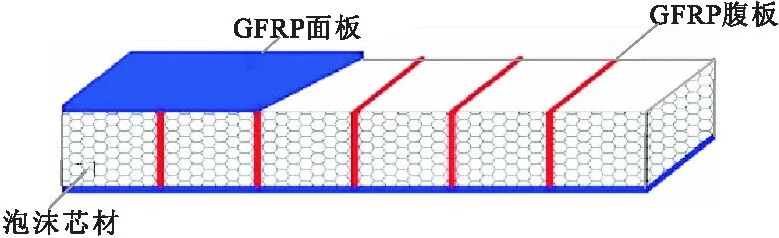
图1 夹层板示意
1.2 材料性能
夹芯板的芯材采用无锡市科招新材料科技有限公司生产的硬质聚氨酯泡沫,密度为60 kg/m3;构件的面板与腹板使用常州市诺博复合材料有限公司生产的[0/90°]正交玻璃纤维布与常州华科聚合物股份有限公司生产的不饱和聚酯树脂。目前制作复合材料构件的工艺主要有手糊成型、真空导入、挤拉成型等;其中真空导入工艺相较于其他工艺具有强度高、刚度高、构件性能的一致性高、树脂用量少等优点。故本次试件采用真空导入成型工艺[10]加工完成。
其基本流程为:(1)切割泡沫得到满足要求的小块;(2)用[0/90°]的玻璃纤维布包裹芯材块,并用玻璃纤维丝捆扎;(3)根据试件要求铺设上下面板所需的玻璃纤维布;(4)铺设脱模布、导流布和导流管;(5)真空袋密封,抽成真空导入树脂;(6)室温固化24~48 h后脱模,按照尺寸需求使用推台锯切割试块。
构件制作过程如图2所示。泡沫芯材的相关材料性能参数在表1中给出。

图2 构件制备流程

性能弹性模量极限强度压缩9.330.36剪切4.10.228
2 静力试验及结果分析

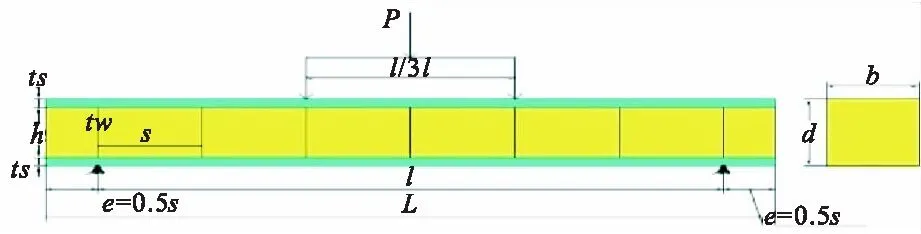
图3 加载示意

图4 静力试验荷载-位移曲线
3 疲劳试验及结果分析
3.1 疲劳试验
疲劳试验同样使用MTS-370型电液伺服疲劳试验机进行加载,采用力控制的模式进行加载。加载方式采用如图5所示的正弦波谱,等幅均匀加载。载荷等级由疲劳试验中最大力与静载试验破坏力的比值r=Pmax/Pu确定,载荷比由疲劳试验加载中最小力与最大力的比值R=Pmin/Pmax确定。本次试验采用0.6, 0.75, 0.9三种载荷等级进行试验,以便观测在不同载荷等级作用下夹层板的疲劳性能。为防止高载荷比下试件的过早破坏,本次试验载荷比为0.2[9]。试验加载频率为2 Hz。试验中使用MTS试验机配套的引伸计来测量夹层板跨中的位移,力与位移均通过MTS公司的Flex Text40采集器在每个循环出现力的极值时,采集力与位移的信息并记录循环数。15个试件中,T1~T5完成载荷等级r=0.6的试验,T6~T10完成r=0.75的试验,T11~T15完成r=0.9的试验。
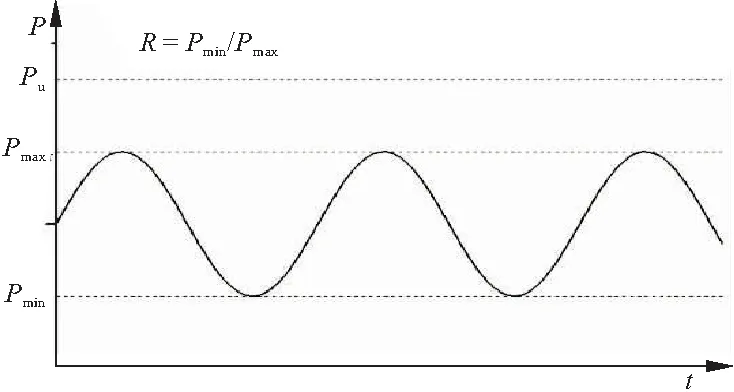
图5 疲劳荷载加载形式
图6为试验中构件所发生的变化,试件在3种不同载荷等级下均呈现类似的破坏模式。随着循环次数的增加,泡沫芯材的抗剪承载力逐显不足,导致在与弯矩的共同作用下试件的边跨泡沫首先出现45°的斜裂纹(图6b),随后泡沫与格构腹板之间出现脱粘间隙(图6c)。腹板的存在限制了裂纹与脱粘现象的发展,使其局限于各自的区块之内,无法延伸到相邻的腹板当中。试验中第二块腹板与第六块腹板两边的泡沫逐渐退出工作,使得这两块腹板独立承受荷载作用,腹板出现失稳倾斜的情况,即底端向夹芯板中部倾斜、顶端向板端倾斜。最后的破坏形态,载荷等级较低(0.6, 0.75)的两组构件由于上面板受压屈服,导致板的挠度不断增大,在其挠度超过30 mm时判定试件失效。而载荷等级0.9的构件经推测由于剪力较大,腹板内部的轴向拉应力过大,引起上述两块腹板的应力集中处与面板分层,导致整个板的承载力急速下降,试件直接破坏。

图6 疲劳试验加载过程
3.2 结果分析
3.2.1疲劳寿命统计分析
由于疲劳试验结果存在较大的离散性,而疲劳设计中又要求提供准确、可靠的疲劳性能数据,所以必须借助统计学方法合理地处理试验结果。S-N曲线是用来描述试件疲劳性能最直观有效的一种方法,它从宏观现象的角度来反映试件的疲劳性能,避免了对试件内部微观复杂现象的考虑,有很强的工程应用价值。目前常用的有如下三种形式的S-N曲线:(1)一般经验模型,即幂函数、指数函数模型;(2)基于正态分布或Weibull分布的模型;(3)基于刚度或强度退化理论下的S-N曲线模型。
其中,Weibull分布模型具有较大的使用范围,而且Weibull概率密度函数存在有最小安全寿命。故此本文采用Weibull分布来分析复合材料格构增强夹芯板的疲劳寿命分布[11]。不同载荷等级作用下,复合材料夹芯板的寿命如表2所示。

表2 腹板增强复合材料夹芯板疲劳试验结果
3.2.2Weibull疲劳寿命分布模型
在同一循环荷载作用下,试件的疲劳寿命N可以用以下Weibull概率密度函数来表示:
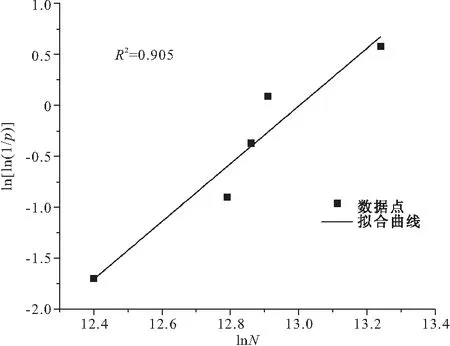
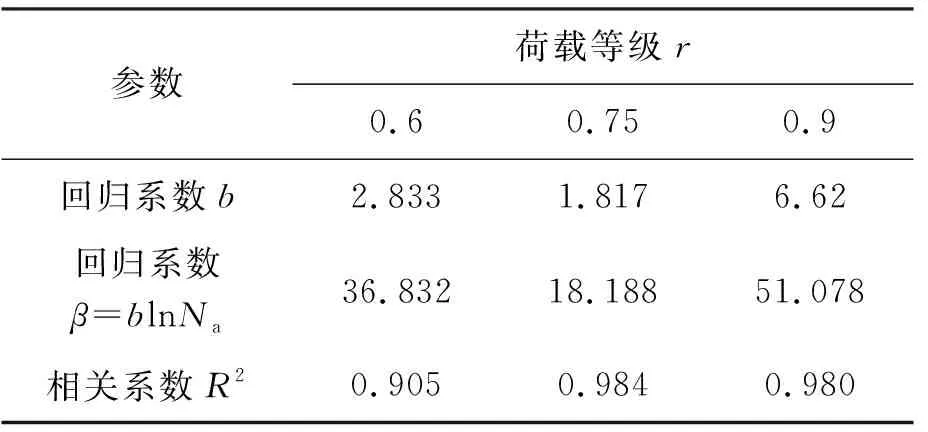
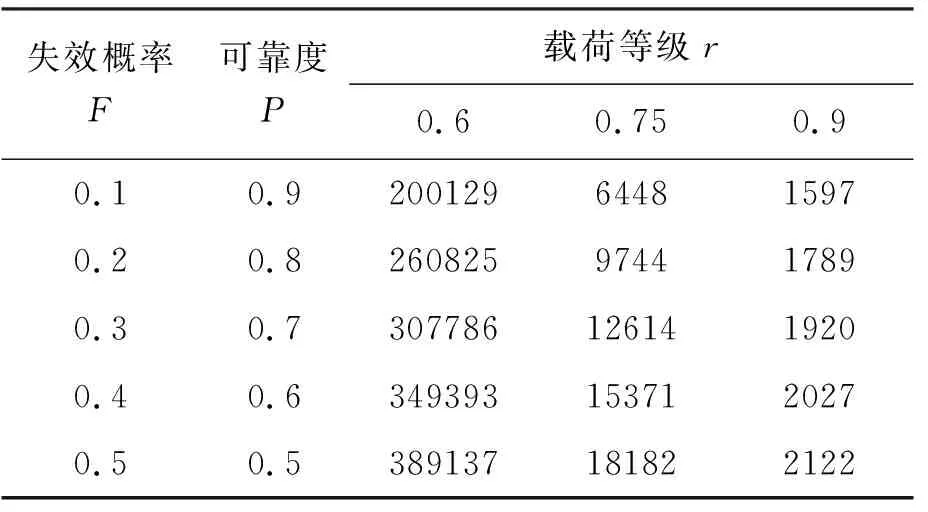
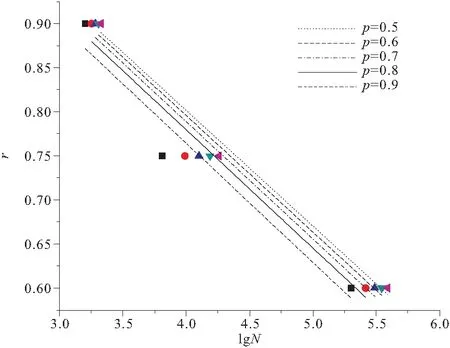
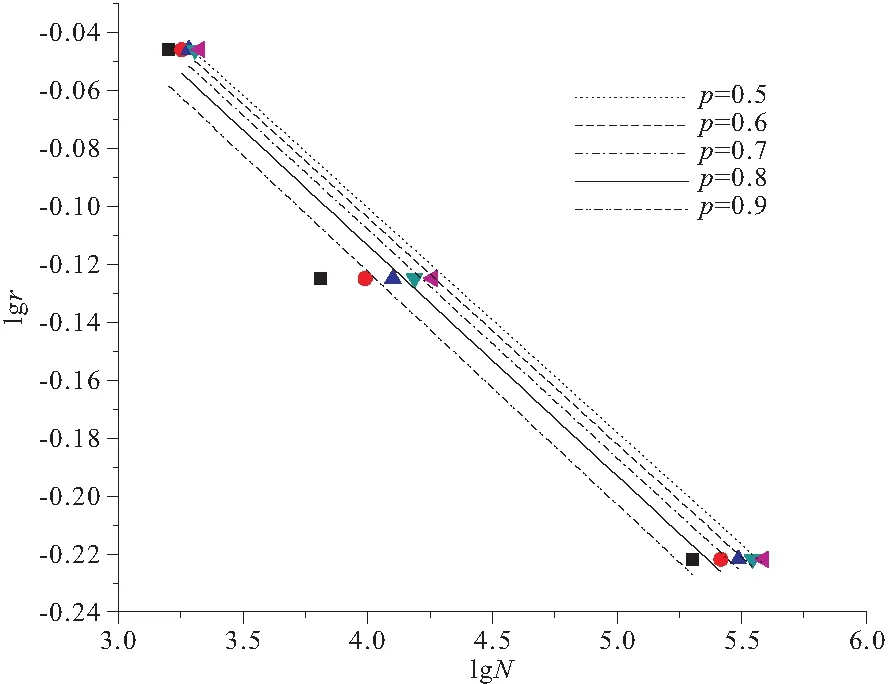
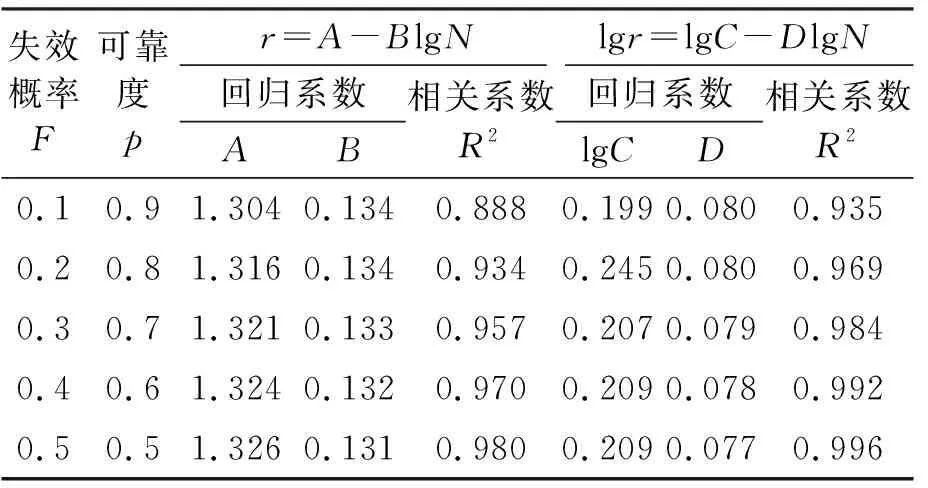
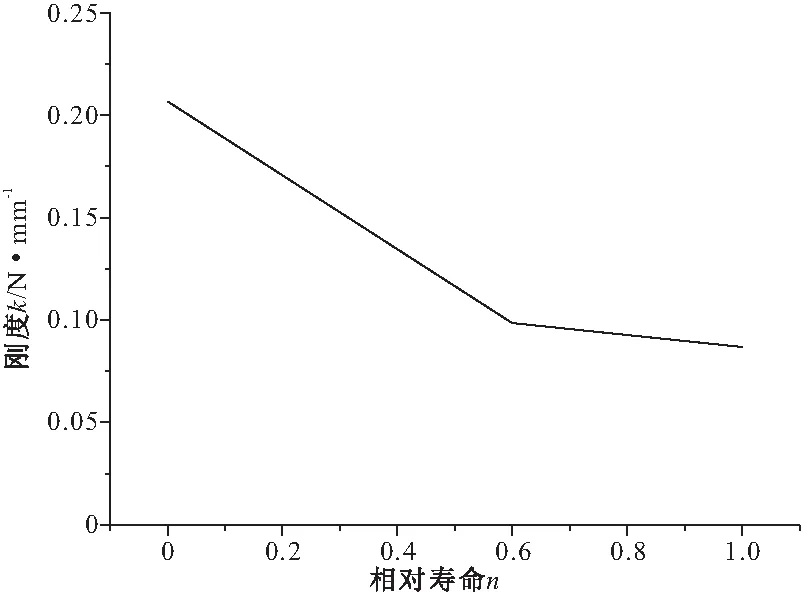
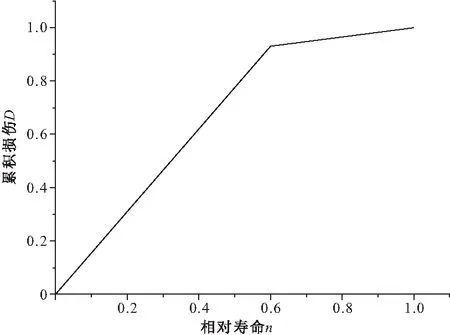
N0 (1) 式中:b为Weibull形状参数;Na为特征寿命参数,即存活率为36.8%时的寿命;N0为最小寿命参数。Weibull分布模型是一个三参数的非线性化模型,它比一般的线性模型能更完善地拟合试验数据点。 按Weibull分布的随机变量即Weibull变量表示为Np。由式(1)的密度函数可以得出Np的分布函数f(Np)为: (2) 则可靠度p的超值累积频率函数为: (3) Weibull分布模型中有b,Na,N0这样三个参数,在既知三个参数具体值和给定可靠度p的情况下,我们可以得到此种构件可靠度为p时的疲劳寿命Np。 本文假定夹层板的最小寿命为0,这样就可以将三参数的模型简化为两参数模型,式(1),(3)可以写成: (4) (5) 将式(5)进行变换可得: (6) 对式(6)的两边取两次对数: (7) Y=bX-β (8) 式(8)可以用来检验试验数据服从两参数Weibull分布的假设是否合理。式(8)为线性方程,且式中的b,β可以直接从拟合的曲线上得到。若Y,X呈现良好的线性统计关系,则说明两参数的Weibull模型成立。 疲劳寿命Np所对应的可靠度p用下式求得: (9) 式中:K为试件某一载荷等级下所进行的疲劳试验次数,将这些试验按疲劳循环的大小由小到大标号为i,i=1,2,3,…,K。 对表2中的疲劳试验结果进行Weibull分布检验,以载荷等级r=0.6的试件为例,其X与Y如表3所示。 图7为横向格构复合材料夹芯板的Weibull分布检验图,从图中能看出X与Y呈现出良好的线性统计关系,其相关系数R2为0.905。表4为各载荷等级下Weibull分布的回归系数与相关系数,表明了夹芯板能较好的符合两参数的Weibull分布。 图7 r=0.6时 Weibull分布检验 参数荷载等级r0.60.750.9回归系数b2.8331.8176.62回归系数β=blnNa36.83218.18851.078相关系数R20.9050.9840.980 3.2.3考虑失效概率的疲劳方程 传统意义上的S-N方程只有50%的保证率,由上文可知,夹芯板的疲劳寿命Np服从双参数的Weibull分布。将表3中的系数代入式(1),可求出在给定可靠度p情况下的疲劳寿命Np,如表5所列。 表5 不同载荷等级r下疲劳寿命随可靠度p的变化 工程实际中载荷等级r与等效疲劳寿命N有以下两种基本形式: 单对数形公式:r=A-BlgN (10) 双对数形公式:lgr=lgC-DlgN (11) 由表4可绘出在一定可靠度下的疲劳寿命方程即p-r-lgN曲线(图8)和p-lgr-lgN曲线(图9),并以此得出式(10),(11)各项系数的值,具体结果列于表6。 图8 p-r-lgN曲线 图9 p-lgr-lgN曲线 失效概率F可靠度pr=A-BlgNlgr=lgC-DlgN回归系数AB相关系数R2回归系数lgCD相关系数R20.10.91.3040.1340.8880.1990.0800.9350.20.81.3160.1340.9340.2450.0800.9690.30.71.3210.1330.9570.2070.0790.9840.40.61.3240.1320.9700.2090.0780.9920.50.51.3260.1310.9800.2090.0770.996 表4中除了可靠度0.9的情况,p-r-lgN曲线的相关系数R2均大于0.9。说明两种形式的疲劳方程具有良好的拟合度,且式(10),(11)中的线性关系成立。双对数形式的疲劳方程拟合度高于单对数形公式。两种形式的疲劳方程,在不同可靠度下的曲线均有相似的斜率。式(10),(11)中,可将B与D作为常量来处理,分别取值为0.133与0.079。 3.2.4损伤模型推导 本文基于Lemaitre线性损伤准则进行损伤模型的推导。该理论以应变等效为理论基础,将材料的弹性模量作为衡量材料累积损伤的标准[12]。 (12) 腹板增强复合材料夹芯板的初始刚度可用式(13)表示[13] (13) 式中:Kbs为夹芯板的初始刚度;d为夹芯板宽度;h为芯材高度;ts为面板的厚度;Es为芯材的等效弹性模量,与腹板的排列和厚度相关。 假设式(13)中试件的几何参数是恒定的,试件在疲劳过程中只有材料的弹性模量是变化的,综合公式(12),(13)可得 (14) (15) 图10为此种试件的刚度-相对寿命曲线。 次数;N为试件的最大疲劳寿命。由于载荷等级为0.6及0.75时数据量过大,在r=0.6时每200个数据点取一个进行运算,r=0.75时每100个数据点取点代入计算。由图可知,所有试件的刚度退化过程分为明显的两个阶段,刚度持续下降段与刚度平稳段。刚度下降段并非光滑下降而是呈现一定的台阶下降,其原因为格构腹板的存在使得每一块被腹板分隔的泡沫出现裂缝时,裂缝不能扩展到整个试件但形成了可以贯通上下面层的裂缝,试件的内力重分布,腹板参与到板的抗剪当中,试件不会出现明显的脆性破坏,板的变形能力大大提升,使得载荷等级为0.6与0.75的试件出现了刚度相对较长稳定的阶段。在刚度平稳段时,试件的挠度却持续的增加,推测是由于试件上表面的纤维受压出现局部屈服,形成了可绕一定角度转动的塑性铰所致。r=0.9的试件稳定阶段较短,其原因为试件内力过大导致腹板与面层出现分层引起试件的迅速破坏。图中,r=0.9的试件初始刚度明显低于另外两种试件,推测是由于其在第100次循环时其内部已发生破坏所致。 图10 夹层板刚度-相对寿命曲线 将3种载荷等级下的曲线分段最小二乘拟合,如图11,得到格构腹板增强泡沫复合材料夹芯板的刚度退化分段公式 图11 夹层板刚度-相对寿命拟合曲线 (16) 将式(16)代入式(14)当中可以得到夹芯板的累积损伤公式 (17) 式中:D(n)为构件疲劳累积损伤值;α为一无量纲系数。 根据边界条件n=0,D=0;n=1,D=1,可以得到系数α的值为1.72,得到下式: (18) 式(18)给出了刚度与相对寿命之间的关系,如图12所示,故只需要进行一定次数的疲劳循环,就能预测得到构件的疲劳寿命。 图12 夹层板累积损伤过程 3.2.5基于刚度退化的疲劳寿命预测 选取一定的加载次数后,以构件的刚度值为依据计算试件的理论疲劳寿命,并与试验结果进行对比,结果如表7所示,T5预测寿命超过疲劳极限的100万次,为个别偏大数据。 表7 基于刚度退化的疲劳寿命预测结果 从结果可见,刚度退化模型存在着较大的个体差异性,低载荷等级下的预测结果往往超过试件实际寿命,这是由于在较低载荷等级的试验条件下,夹芯板的芯材能较好的抵抗循环荷载,腹板较晚才参与抗剪作用,使得试件试验初期能够较好的维持其刚度,而当芯材开裂泡沫退出工作后,刚度下降,最后与其他载荷比下夹芯板刚度保持一致。载荷等级为0.75及0.9时,预测寿命结果往往小于实际寿命且差距不大,刚度退化模型偏于安全,其能够较好的反应夹层板疲劳寿命。 本研究对格构增强型泡沫夹芯复合材料单向板进行了静力与疲劳四点弯曲试验,对试验得到的疲劳寿命进行了概率学统计处理。研究结论如下: (1) 格构腹板有效的提高了泡沫夹芯复合材料板芯材与面板之间的抗剥离性能,其静力弯曲破坏模式一般为芯材的剪切破坏,试验结果与经典夹层板理论吻合较好。 (2) 格构增强型泡沫夹芯复合材料板在三种载荷等级的测试下均出现了近似的破坏过程。在较低载荷等级下,破坏模式主要为面板的屈服,而高载荷等级下,破坏模式主要为面板的鼓起以及腹板与面板之间的分层。 (3) 格构增强型泡沫夹芯复合材料板的寿命统计能较好的服从Weibull分布,线性相关性达到了0.9以上。 (4)本文通过概率统计方法得到了格构增强型泡沫夹芯复合材料板在一定可靠度下的双对数形式与单对数形式疲劳方程,能够很好的满足工程实际应用。 (5) 本文给出了基于累积损伤模型下的疲劳寿命预测模型,该模型在载荷等级较高的条件下能较好的预测寿命,其所需使用的试验数据较少,且试验数据易于观测,在实际应用中有一定的价值。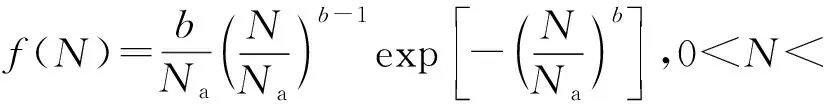

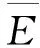
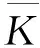



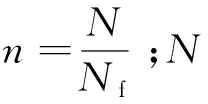
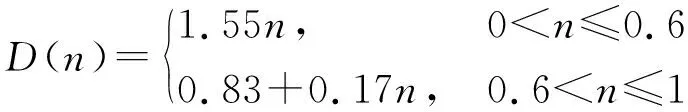

4 结 论
