考虑参数非均匀性的深基坑悬挂式封闭止水体阻水效果分析
2019-03-02徐光彬桂志鹏鞠洪涛
徐光彬, 翟 伟, 桂志鹏, 姜 文, 鞠洪涛
(1. 湖北省电力勘测设计院有限公司, 湖北 武汉 430040; 2. 华中科技大学 土木工程与力学学院, 湖北 武汉 430074)
随着城市化进程的加快,各种复杂地质条件下的深基坑工程也逐渐增多。以武汉地区为例,地质条件最为复杂的当属长江I级阶地区域,由于临近长江,该区域地下水具有承压水头高、水力补充丰沛、含水层深厚等特征[1],处理不当时易发生坑内渗水、突涌等工程问题,给深基坑施工带来极大的风险。因此,对于该区域的深基坑工程而言,采取合理的地下水控制措施就显得尤为重要。工程实践表明,采用悬挂式止水帷幕配合坑底被动区加固(下文简称为封闭式止水体)措施不仅能有效解决长江I级阶地区域深基坑施工面临的地下水问题[2,3],而且与落底式止水帷幕相比表现出明显的价格优势。
然而,无论采用深层搅拌桩或者高压旋喷桩施工封闭式止水体,其作为一种人工材料,不仅包含了土体本身材料属性的变异性,同时受到施工过程中不确定性及后期养护条件不确定性的影响[4,5],使得封闭式止水体的材性参数具有很强的空间变异性[6,7],从而对工程特性产生一系列不确定性的影响。现有的考虑参数空间变异性对工程影响的研究大多集中于自然土体考虑强度参数变异性领域,有关考虑渗透性参数空间变异性对工程影响的研究也多集中于边坡、土石坝稳定性分析方面[8~10],而考虑渗透性参数空间变异性对止水帷幕阻水效果影响的研究则基本未见报道。
因此,本文针对上述问题,首先在确定性分析的前提下,对不同设计参数封闭式止水体的阻水效果进行分析;其次基于随机场理论,开展考虑渗透系数空间变异性对深基坑悬挂式封闭止水体阻水效果影响的研究。
1 问题描述
1.1 工程概况
本文依托武汉某电缆隧道深基坑工程,基坑深15.3 m,直径10.4 m,采用沉井法施工,止水结构为悬挂式止水帷幕+坑底被动区加固兼作水平向止水体,止水帷幕及坑底加固区采用Φ850@600三轴搅拌桩,坑底加固区厚度为8 m。由于研究核心在于渗透系数变异性对封闭式止水体阻水效果的影响,对围护结构的描述从略,详细的悬挂式封闭止水体结构示意图如图1所示。

图1 止水结构示意/m
1.2 水文地质
该基坑位于长江I级阶地前缘,表层为松散的人工填土;上部主要为黏性土与粉砂层;下部为粉砂层、细砂层和强风化泥岩,详细的土体参数见表1。粉砂层、细砂层为承压含水层,承压水水头位于地表以下3 m处,承压水与长江水连通。
1.3 水文地质
考虑到随机有限差分及渗流计算的耗时性,本文仅截取止水结构二维模型进行分析,建立如图2所示的FLAC3D数值模型,模型尺寸为100 m×1 m×60 m。土体、悬挂式止水帷幕和坑底加固区采用实体单元模拟,同时考虑到封闭式止水体为考虑参数随机场的主要研究区域,网格需要进一步加密。

表1 土体材料参数

图2 FLAC3D数值模型
整个模型的渗流边界条件为:下边界及岩层设为不透水层,左边界为透水边界且根据地下水情况设为定水头边界(即考虑长江水力补充),上边界设置为孔隙水压力为0的透水边界。
模拟过程为在初始水位条件下坑内一步降水至加固区顶面,监测在此过程中止水帷幕以及加固区顶的渗水量,待达到渗流平衡时,统计工作井单位时间内的渗水量,由于统计得到的是二维模型的渗水量,需要通过积分转化为圆形深基坑的单位时间渗水量,下文所述渗水量均为已转化后整个深基坑范围内的渗水量。
2 封闭式止水体阻水效果确定性分析
对于本文工程实例而言,加固区厚度设计值为8 m,可能过于保守,因此本文基于确定性分析方法(即不考虑渗透系数的空间变异性),对不同设计参数的封闭式止水体的止水效果作出分析。设计过程中,可调整幅度较大的参数包括加固区厚度和止水结构渗透系数,分别探究两个因素对阻水效果的影响。加固区厚度设置7个厚度值,分别为1,1.5,2,3,4,6,8 m;渗透系数根据经验取值为1.0×10-5,5.0×10-5,7.0×10-5,1.0×10-4cm/s,共计7×4=28种工况。
图3为渗透系数等于1.0×10-4cm/s时,渗水量随加固区厚度变化的曲线。可以看出,随着加固区厚度的增加,止水帷幕渗水量基本不变,说明加固区厚度对止水帷幕阻水效果没有影响。另一方面,随着加固区厚度的增加,加固区顶面渗水量逐渐减小,但是存在一个临界厚度值,当厚度大于该值时,增加厚度对阻水效果不再有增益作用。

图3 渗水量随加固区厚度变化曲线
图4为临界厚度随阻水体渗透系数不同的变化曲线,整体而言,临界厚度随着渗透系数的增大而增大,但即使渗透系数等于1.0×10-4cm/s时,临界厚度也仅为4 m,说明原设计方法中8 m厚的加固区厚度过于保守。
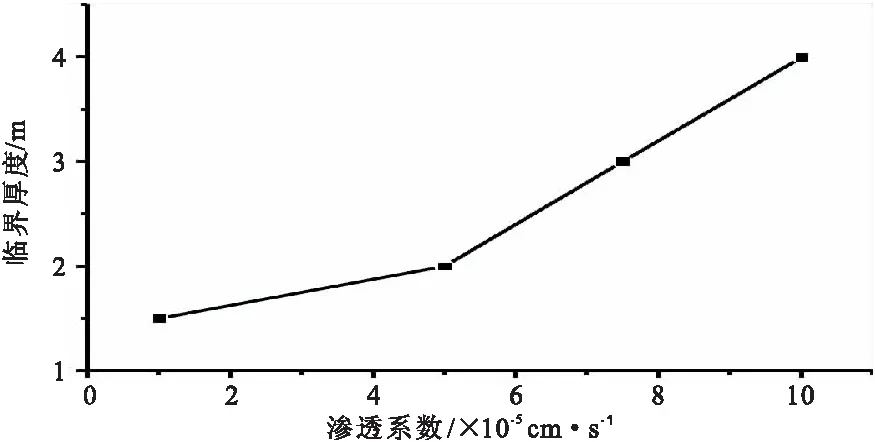
图4 临界厚度随渗透系数变化曲线
图5为渗透系数等于1.0×10-4cm/s时,不同加固区厚度情况下的渗流场。可以看出,当加固区厚度小于临界厚度时,承压水透过底部加固区渗入坑内;当厚度逐渐增大时,经由加固区渗入坑内的水越来越少,中间的渗入量趋近于0,此时增大加固区厚度对于减小渗入量十分有利且效果显著;而当加固区厚度持续增大至超过临界厚度时,加固区近似于不透水材料,承压水主要经由加固区与止水帷幕交界处渗入坑内,而这一涌水量相对固定,因此增大加固区厚度对于减小渗流量的效果并不明显。

图5 不同加固区厚度渗流场
3 渗透系数空间变异性对封闭式止水体阻水效果影响分析
基于前文分析可知,当渗透系数取最不利情况分析(1.0×10-4cm/s)时,加固区的临界厚度等于4 m。本文在此基础上,认为加固区厚度等于4 m,展开考虑水泥土渗透系数空间变异性对封闭式阻水体止水效果影响的研究。
采用随机场理论来描述岩土体参数空间变异性已在业界形成共识。各种生成随机场的方法也都比较成熟,常见的有局部平均法[11]、中心点法[12]、谱分解法[13]、Karhunen-Loeve(K-L)级数展开法[14,15]等。K-L级数展开法具有所需离散的随机变量数目较少、运算效率高、网格单元离散与所研究的问题不耦合等优点。因此,本文采用K-L级数展开法生成随机场,其具体生成方法及原理详见文献[14~16]。
水泥土渗透系数变异系数COV范围在0.2~0.9之间[17],相较于自然土体而言变异性更强,且本文的研究重点为封闭式止水体的阻水效果,因此仅考虑封闭式止水体渗透系数的空间变异性,自然土体的渗透系数则视作均值。
关于封闭式止水体渗透系数空间变异性特征取值,需要做以下几点说明:(1)关于水泥土渗透系数的分布形式,尚未发现文献提及,因此参照对水泥土无侧限抗压强度分布形式的研究[18],认为其满足正态分布或对数正态分布,又由于地质参数具有非负性,选取对数正态分布作为渗透系数变异性的分布形式。(2)水泥土渗透系数的变异系数COV在0.2~0.9范围内,本文取COV=0.7进行分析。(3)关于水泥土渗透系数相关距离范围的研究较少,更多的是关于其无侧限抗压强度空间变异性指标的研究,一般认为,对深层搅拌桩技术而言,其强度参数水平向相关距离在0.4~1.2 m范围内,竖向相关距离在1~4 m范围内[19,20],且随着相关距离的增大,工程风险逐渐增大,因此本文参考水泥土强度指标的相关距离范围,取渗透系数水平向相关距离为0.8 m,竖向相关距离为4 m。(4)渗透系数均值按照最不利情况取值,即等于1.0×10-4cm/s。最后,基于上述空间变异性特征参数,进行2000次蒙特卡洛模拟。
图6为渗透系数随机场的一次典型实现(FLAC3D中渗透系数与常规渗透系数单位cm/s间换算关系为×10-6),可以看出其分布呈现明显的空间变异性特征,进一步检验其均值和标准差,均与预设值相符,证明本文生成的渗透系数随机场是正确有效的。同时,观察考虑渗透系数空间变异性情况下的渗流场,可以看出由于渗透系数分布的不均匀性,渗流量的大小也是分布不均的。若渗透系数较大的区域出现在水力梯度最大的地方(止水帷幕与加固区交界位置),则会明显增加坑内渗水量,带来严重的工程隐患。
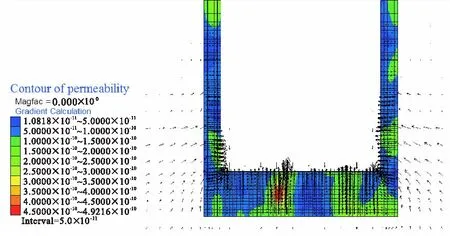
图6 典型渗透系数随机场及对应渗流场
由图7可以看出,加固区顶面、止水帷幕和总的渗水量均呈现变量形式,且变异系数分别为4.9%,7.4%,4.6%,说明渗透系数空间变异性的存在会给基坑渗水量带来不确定性,且对止水帷幕的阻水效果影响最为明显。此外,对其分布形式进行卡方检验,在显著水平为0.1的条件下,正态分布和对数正态分布的p值(p值表示分布拟合检验的拟合程度高低,p值越大,拟合效果越好)均大于0.1,因此可以认为渗水量分布满足正态分布或对数正态分布形式。同时,两种分布的p值较为接近,且对于低概率区域而言,两种分布形式的概率近似相等,考虑到正态分布表达形式更为简便,下文的分析讨论均认为渗水量分布满足正态分布形式。

图7 渗水量概率密度直方图
对比确定性分析和考虑渗透系数空间变异性的结果可以发现,若将渗水量作为正态分布形式的变量分析,确定性分析结果分别会有95%的概率高估加固区顶面渗水量、78%的概率高估止水帷幕渗水量以及70%的概率高估总渗水量。通常而言,考虑参数空间变异性后的计算结果(例如围护结构挠曲变形、地表沉降等指标)均值往往会比确定性分析的计算结果大,但对于本文问题来说,考虑渗透系数空间变异性反而会使不确定性计算结果均值小于确定性计算结果,该现象可做如下解释。
对于成层土,竖直方向的等效渗透系数可通过式(1)计算。
(1)
式中:ky为等效渗透系数;H为土层总厚度;kiy为分层土的渗透系数;Hi为分层土厚度。
以两层土计算平均渗透系数为例,若H1=H2=1 m,k1y=k2y=5×10-5cm/s,相当于不考虑渗透系数空间变异性的情况,即确定性分析,此时ky=5×10-5cm/s;而当考虑渗透系数的空间变异性时,假设k1y,k2y变化相同幅值(保持渗透系数均值不变),此时k1y=4×10-5cm/s,k2y=6×10-5cm/s,计算所得ky=4.8×10-5cm/s。可以看出考虑不均匀性后等效渗透系数是减小的,由此可以解释为何考虑渗透系数空间变异性时渗水量反而会大概率低于确定性分析的计算结果。而对于考虑变异性时渗水量大于确定性分析结果,则可能由于止水体内部形成了连续的高渗透性区域,从而导致渗水量较大。
4 结 论
论文首先探究了封闭式止水体设计参数对其阻水效果的影响,其次基于随机场理论,开展了考虑渗透系数空间变异性对深基坑悬挂式封闭止水体阻水效果的研究。得到如下结论:
(1)加固区存在一个临界厚度值,当厚度超过该值时,增加厚度对提升阻水效果并无增益。
(2)渗透系数空间变异性对悬挂式封闭止水体阻水效果影响较为显著。考虑渗透系数空间变异性会使不确定性计算结果均值小于确定性计算结果。
