钢骨混凝土桥墩撞击抗剪强度计算模型

李清阳， 张 南， 李界全， 高 闵， 陈佳佳， 沙笑笑

(南京工业大学 土木工程学院， 江苏 南京 211816)

近年来，桥梁受到车、船的撞击事故频繁发生，造成了人员伤亡和经济损失等严重后果，因此桥梁的抗撞击性能研究成为了工程界以及学术界高度关注的热点[1]。在桥梁碰撞事故中，由于撞击过程在瞬间完成，材料变形速度很快，应变率效应对材料的强度以及构件的承载力有很大的影响[2]。因此研究桥墩的撞击抗剪强度，对桥梁的抗撞击性能研究和城市交通安全具有重大意义。

国内外学者一直在对钢筋混凝土构件的受剪理论进行研究，目的是为了合理地解释其受剪机理，其中修正压力场理论逐渐得到学术界的肯定。该理论由Collins等首次提出，经过多年的发展，CSA A23.3-94《加拿大混凝土结构设计标准》中构件抗剪计算方法就是以该理论为基础[3～7]。魏巍巍等[8]基于修正压力场理论，建立了钢筋混凝土梁的抗剪承载力计算方法；朱伟庆等[9]在修正压力场理论的基础上，采用正截面分析法建立高强度型钢混凝土柱的受剪计算模型。

同时钢骨混凝土结构由于具有很高的强度和刚度以及较好局部和整体稳定性，因此越来越受到工程界的青睐。李俊华等[10]进行了型钢混凝土柱抗剪性能试验研究；张莉杰等[11]采用叠加原理提出钢骨混凝土桥墩斜截面承载力计算公式；张南等[12]进行不同配钢形式的钢骨混凝土桥墩撞击试验，提出撞击力峰值与抗撞强度之间的等效系数。目前对钢骨混凝土桥墩撞击抗剪强度研究并不常见，为了深入了解钢骨混凝土桥墩抗撞性能，本文进行了钢骨混凝土桥墩水平撞击试验，建立钢骨混凝土桥墩撞击抗剪强度计算模型。

1 试验概况

1.1 试验装置及内容

本文的试验模型参考桥梁实际尺寸，按一定比例设计了6根桥墩试验模型(编号分别为D-1～D-6)，进行了车辆水平撞击试验。撞击点位置参考车辆撞击桥墩的作用范围，本文的试验装置如图1a所示。其中，D-1为普通钢筋混凝土桥墩，D-2为内置角钢混凝土桥墩，D-3和D-5为截面相同的内置槽钢混凝土桥墩，D-4和D-6为截面相同内置双圆钢管混凝土桥墩，截面如图1b～1e所示。桥墩试件内部由钢骨和斜撑焊接形成钢骨架，各桥墩模型截面纵向配筋率均为3.87%，D-2，D-3，D-4的横向钢骨等效配钢率分别为0.59%，0.49%，0.76%。模拟桥梁上部结构荷载，墩顶施加水平方向约束，按0.1的轴压比施加竖向力，桥墩模型简化成顶端简支，底端固支的超静定结构，如图1f所示。桥墩模型的钢材性能如表1所示，表中：fy为钢材屈服强度；Es为钢材弹性模量。

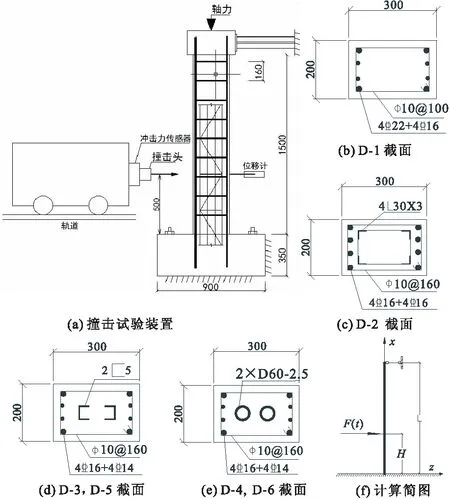
图1 桥墩模型撞击试验示意图/mm

钢材种类101212141622fy/MPa379406486454412472Es/×105 MPa2.02.02.02.02.02.0

1.2 试验结果与分析

1.2.1试验结果

通过改变落锤的高度来获得撞击能量，桥墩模型破坏形态如图2所示。6根桥墩模型在水平撞击荷载下均发生剪切破坏，撞击点至桥墩根部出现了斜裂缝，同时撞击点背面出现水平裂缝。

图2 桥墩模型撞击破坏形态

对比图2中的破坏形态可知，普通钢筋混凝土桥墩模型主要有一条较宽的斜裂缝，裂缝处混凝土发生剥落；内置角钢、内置槽钢以及内置双圆钢管的混凝土桥墩模型均出现多条斜裂缝。说明内置钢骨与箍筋形成骨架，对受剪核心区混凝土提供很好的约束作用，抑制了斜裂缝的发展；同时相比于钢筋混凝土桥墩模型，内置钢骨混凝土桥墩模型的斜裂缝数量较多、宽度较小，表明加入内置的钢骨改善了桥墩剪切破坏时的脆性特征，延性较好。

1.2.2撞击力分析

图3为 D-1～D-6破坏阶段的撞击力时程曲线，撞击力时程曲线可分为峰值段和缓冲段，对结构产生作用的峰值段持续时间约20 ms。

图3 撞击力时程曲线

6根桥墩模型撞击破坏峰值力如表2所示，从表2中可知，相比于D-1(普通钢筋)的撞击破坏峰值力，D-2(内置角钢)提高了24.05%，D-3(内置槽钢)提高了17.52%，D-4(内置双圆钢管)提高了25.51%，D-5(内置槽钢)提高了19.78%，D-6(内置双圆钢管)提高了20.61%。因此可见，由于加入了内置钢骨，显著提高了混凝土桥墩的抗撞击强度，钢骨混凝土桥墩比钢筋混凝土桥墩有较好的抗撞击性能。

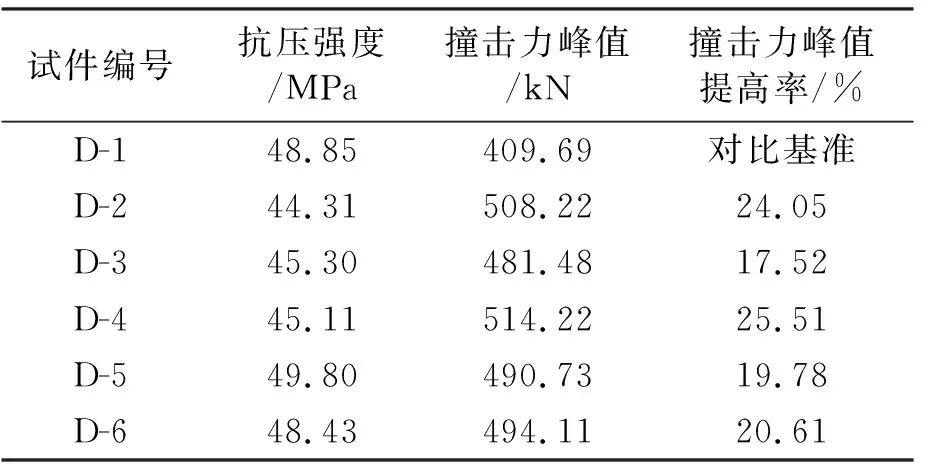
表2 桥墩模型撞击峰值力对比

撞击过程是一个瞬态过程，撞击力峰值出现在撞击过程的某一时刻，桥墩模型的破坏荷载并非撞击力时程曲线的峰值。目前工程设计中将撞击力峰值等效成一个等效静力来进行抗撞设计。张南等[12]定义一个撞击强度等效系数Kd，Kd取1.25，即如式(1)所示：

Fd=Fm,d/Kd

(1)

式中：Fm,d为撞击力峰值；Fd为等效撞击力。

等效撞击力并非桥墩的撞击抗剪承载力，根据图1f中计算简图得到桥墩模型任意截面的动弯矩方程和动剪力方程如式(2)，(3)，将等效撞击力带入式(2)，(3)中计算得出等效剪力Q(x,t)和等效弯矩M(x,t)。

(2)

(3)

2 钢骨混凝土桥墩受剪模型

2.1 材料的动态力学性能

相关文献表明，当混凝土的应变速率增加时，其抗拉(压)强度以及弹性模量均有所提高，但峰值应变和极限应变没有变化；钢材的屈服强度会随着应变率的增加有所提高，但泊松比和弹性模量基本不变。本文材料动态强度的分析采用欧洲规范的率型经验公式[2]。

2.1.1混凝土和钢材动态力学性能

混凝土动态抗压强度按式(4)计算。

(4)

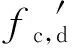
混凝土的动态弹性模量可表示为：

(5)

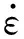
钢材的动态抗拉(压)强度可表示为：

(6)

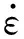
2.1.2平均应变率计算

图4为水平撞击试验测得D-4钢筋应变片和混凝土应变片在不同撞击能量下的应变时程曲线，其中钢筋1号片位于撞击点正背面的纵筋上；混凝土1号片位于撞击点正背面。

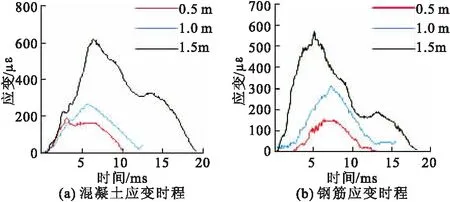
图4 混凝土与钢筋应变时程曲线

定义一个材料动态强度放大系数Ki，通过撞击试验数据得到撞击荷载下材料的动态力学参数，材料动态强度可表示为：

fi,d=Kifi

(7)

式中：fi,d为材料的动态强度；fi为材料的静态强度。

材料在不同撞击能量下应变率是不同的，通过分析计算可知，在不同撞击能量下，材料的动态强度系数误差在5%左右，误差范围较小，故取材料平均应变率对应的动态强度作为撞击破坏下材料的动态强度，各材料的动力放大系数见表3。

表3 材料强度动力放大系数

2.2 撞击抗剪强度计算模型

本文以修正压力场理论为基础，建立钢骨混凝土桥墩的撞击抗剪强度计算模型，如图5所示。图6和表4列示出了修正压力场的基本方程，表中材料强度均为静态强度，运用式(7)替换成材料的动态强度。表中的应变是各材料的平均应变，在撞击荷载作用下，撞击力峰值在某一时刻超过破坏荷载，使得材料的瞬时应变超过破坏荷载所对应的应变，并且这样的变形是不可恢复的塑形变形，因此桥墩在发生撞击破坏时的变形比静力破坏时要大，因此本文计算模型中所考虑的平均应变是等效撞击力所对应的各材料应变的平均值。

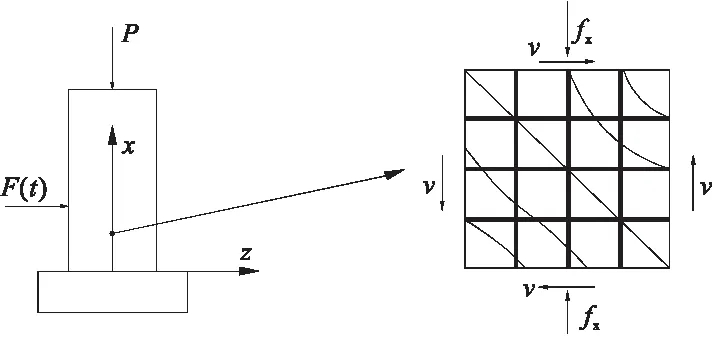
图5 桥墩计算模型

图6 修正压力场理论计算模型

注[8]：fsx，fsz为钢筋纵向和横向的应力；fcx，fcz为混凝土纵向和横向的平均应力；da为骨料粒径；f1为垂直于裂缝方向的平均拉应力；f2为沿裂缝方向的平均压应力；θ为斜压应力角；vas为单元剪应力；εx，εz，γ分别单元纵向平均应变、横向平均应变和平均剪应变；ε1为主拉应变；ε2为主压应变；vci为沿裂缝处的剪应力；w为平均裂缝宽度；sθ为平均裂缝间距

2.2.1变形协调条件

假定桥墩中混凝土和钢材之间符合变形协调条件，即：

εx=εcx=εsx

(8)

εz=εcz=εsz

(9)

γ=γc=γs

(10)

式中：εcx，εcz，γc分为混凝土纵向平均应变、横向平均应变和剪应变；εsx，εsz，γs分为钢材的纵向平均应变、横向平均应变和剪应变。

结合表4中式(e)，(f)，(g)得：

ε1=εx(1+cot2θ)-ε2cot2θ

(11)

2.2.2平衡条件

桥墩受到水平撞击力作用时，纵筋和纵向钢骨承担纵向的拉力，横向钢骨主要承担剪力，则根据平衡条件有：

fx=fcx+ρsxfsx

(12)

fz=fcz+ρszfsz

(13)

v=vc+vas+ρswvsw

(14)

式中：fx，fz，v分别为单元横向应力、纵向应力和剪应力；vc为受压区混凝土剪应力；vsw为横向钢骨剪应力；ρsx，ρsz，ρsw分别为纵向、横向配钢率和横向钢骨等效配钢率。

2.2.3材料应力应变关系

钢筋和混凝土的应力-应变关系采用表4中式(j)，(k)，(m)，(n)，横向钢骨的剪应力-应变关系为：

vsw=Gsw,dγs≤fsw,d

(15)

式中：Gsw,d为钢骨的动态剪切模量；fsw,d为钢骨动态剪切屈服强度。

3 撞击抗剪强度计算方法

桥墩模型受到撞击作用时，剪跨区产生了主斜裂缝，同时由于弯矩的作用产生水平裂缝，因此要考虑受压区混凝土对撞击抗剪强度的贡献。本文的分析同时考虑受压区混凝土对抗剪承载力的贡献、混凝土骨料咬合力以及箍筋和钢骨所承担的剪力。

3.1 受压区混凝土抗剪贡献

受压区撞击抗剪承载力计算模型如图7所示，在钢骨混凝土桥墩中，纵向钢骨和纵筋受拉，根据应变协调条件，可认为纵向钢骨应变与纵筋应变相等，即εwx=εsx。由平衡条件，忽略骨料咬合力的纵向分力，有：

C=εsx(Esv,dAsv+Esw,dAw)

(16)

式中：Esv,d为纵筋的动态弹性模量；Asv为受拉纵筋的截面面积；Esw,d为钢骨的动态弹性模量；Aw为纵向钢骨的截面面积；εsx为纵筋应变。

根据参考文献，受压区合力可表示为[15]：

(17)

得到中和轴高度xn为：

(18)

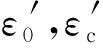
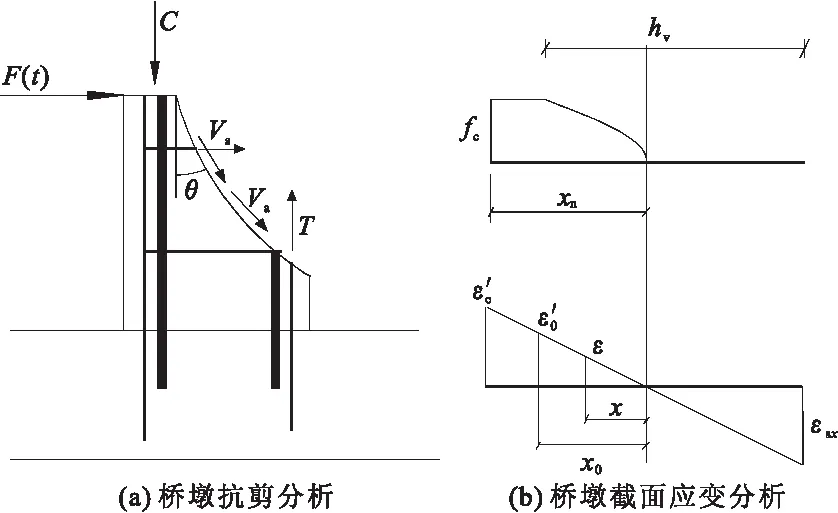
图7 受压区计算模型

钢骨混凝土桥墩受压区混凝土受到压应力fc(ε)和剪应力vc的作用，其破坏符合混凝土双轴受力准则[16]，表达式为：

(19)

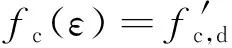
沿中和轴高度积分得到受压区混凝土提供的撞击抗剪承载力为：

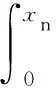
(20)

3.2 撞击抗剪承载力计算

由于桥墩受到撞击力作用，z方向产生的挤压应力很小，故fz=0，联立表4中式(a)和式(13)可得：

vas=f1cotθ+ρszfszcotθ

(21)

将式(21)代入式(14)中得到：

v=vc+f1cotθ+ρszfszcotθ+ρswvsw

(22)

式(22)中第二项为混凝土骨料咬合力，由图8c可知混凝土骨料咬合力包含沿裂缝处的剪应力以及纵筋和纵向钢骨对混凝土的销栓作用，相关文献表明，纵筋和纵向钢骨对混凝土的销栓作用比较小，并且很难确定，因此在文中忽略此影响。钢骨混凝土桥墩剪切破坏时，当箍筋配置适量，混凝土先开裂随后箍筋达到屈服，外围混凝土出现剥落，由于钢骨架的作用，核心混凝土主压应变未达到峰值，裂缝处的剪力vci未达到式表4中式(d)中的最大值，因此可得钢骨混凝土桥墩撞击抗剪承载力为：

(23)

式中：Ayv为箍筋等效截面面积，其中包括斜撑在横向的等效面积；s为箍筋间距；Asw为等效横向钢骨截面面积；fyv,d为箍筋动态抗拉强度。

图8 平均应力与裂缝处局部应力

由图8b中横向平衡可知，桥墩截面中斜压应力使纵筋和纵向钢骨受压，而斜拉应力使纵向钢筋和纵向钢骨受拉，横向不平衡力由箍筋、斜撑以及横向钢骨承担，则有：

(24)

在修正压力场理论中，单元纵向应变εx和斜压应力角θ是十分重要的两个参数，计算过程需要迭代，十分复杂，因此collins提出简化的待定参数εx和θ的表达式如下[6]：

(25)

(26)

式中：sxe为裂缝控制参数，sxe=35sx/(ag+16)，其中sx为相邻纵筋沿截面高度方向的距离；Md，Vd分别为等效剪力和等效弯矩；0.5cotθ可取为1，误差很小；P为轴向力，拉为正，压为负。

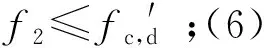
4 模型计算及分析

4.1 计算步骤

由式(26)，(18)，(20)计算得到εsx，xn，Vc,d；再将上述结果与γs代入式(23)得到桥墩撞击抗剪承载力Vd，计算结果见表5，与试验结果较符合。

表5 撞击抗剪承载力计算值与试验值对比

注：Vd,e为试验所得撞击抗剪承载力；Vd,p为计算所得撞击抗剪承载力；η=(Vd,e-Vd,p)/Vd,e

4.2 计算模型对比分析

为了说明本文建立的计算公式是合理的，分别按钢骨组合结构规范、叠加原理、型钢组合结构规范和本文计算方法来计算桥墩撞击抗剪承载力，各材料的强度均采用材性试验的实测数据，并考虑表3中的强度动力放大系数，表6列出计算结果与试验结果的平均误差值。从对比结果看出，各种计算方法的计算结果与试验结果对比的平均误差值分别为23.32%，15.64%，19.37%，13.10%。计算值均比试验结果小，且本文计算方法计算所得结果平均误差值最小。

钢骨规程和型钢规程中的钢骨混凝土柱抗剪承载力计算公式是在考虑混凝土、箍筋和钢骨对抗剪承载力贡献的基础上建立的经验公式，这些经验公式并非要精确预测构件的抗剪承载力，只是为了防止发生剪切破坏；文献[11]中的抗剪计算公式是基于钢骨组合结构规程，运用叠加原理考虑斜筋的贡献。但上述几种计算方法未考虑纵筋率的影响，事实上，适当增加构件的纵筋率，使受压区高度和销栓作用增加，阻止裂缝增长增加混凝土骨料咬合力。本文的计算模型未直接考虑纵筋的销栓作用，但纵筋率增加体现在受压区高度的变化以及混凝土纵向应变εx的减小，使得抗剪强度在适当范围内增加。

εx和θ在本文计算模型中是影响钢骨混凝土桥墩撞击抗剪强度十分重要的因素。钢骨规程中轴压力使得抗剪承载力增加0.07N(N为轴压力)，而本文的计算模型中，当轴压力增大时，结合式(25)，(26)，εx会减小，θ会减小，代入式(23)可知桥墩的撞击抗剪承载力提高；钢骨规程中抗剪承载力是混凝土、箍筋和钢骨承担剪力的线性组合，剪跨比影响线性组合系数，本文模型中，剪跨比影响混凝土斜压应力角θ，当剪跨比较小时，裂缝越接近竖直，即θ变小；当剪跨比较大，裂缝接近水平，θ变大，撞击抗剪承载力Vd发生变化。

表6 不同模型的计算结果对比

5 结 论

(1)通过本文试验结果得出，撞击荷载作用下桥墩发生剪切破坏，加入内置钢骨可以提高桥墩的侧向刚度，抑制桥墩斜裂缝的发展，改善了混凝土桥墩剪切破坏的脆性特征，提高了混凝土桥墩的抗撞击强度，具有较好的抗撞击性能。

(2)钢骨混凝土桥墩撞击抗剪承载力主要由受压区混凝土承担的剪力、混凝土骨料咬合力、箍筋承担的剪力以及横向钢骨承担的剪力四部分组成。本文基于修正压力场理论，考虑受压区混凝土对撞击抗剪承载力的贡献以及应变率效应对材料动态强度的提高，建立撞击抗剪强度计算模型，运用强度动力放大系数Ki来计算材料动态强度；计算表明，受压区混凝土可承受20%～40%的剪力，考虑其对撞击抗剪强度的影响是合理的。

(3)本文模型的计算结果与试验值误差约13.10%，相比较于其他计算方法，与试验值最接近。本文模型用混凝土纵向应变εx和混凝土压应力角θ来考虑轴力，弯矩和剪力对桥墩的耦合作用；同样以上两种参数也体现了轴压力以及剪跨比对撞击抗剪强度的影响。此外，本文模型考虑了纵筋对撞击抗剪强度的影响，纵筋率的适当增加会增加混凝土的骨料咬合力，可以对钢骨混凝土桥墩抗撞设计与分析提供参考。