武器系统作战能力需求满足度评估方法

焦安龙,许俊飞

(1.中国人民解放军91439部队,辽宁 大连 116041;2.海军工程大学,湖北 武汉 430033)

随着海军新型武器系统的快速发展,其作战能力能否满足当前海上作战需求,需对其进行科学的论证。作战能力是表征武器装备完成作战任务的重要指标,武器装备对敌目标进行打击时,对其作战能力有何要求,对这一过程的分析称之为武器系统作战能力需求分析。通过作战能力需求分析可对武器装备提出一系列的性能指标要求,其结果的合理性与科学性对武器装备的发展与建设具有指导性的意义。

目前,对能力需求分析的研究很多,用于能力需求生成的成熟方法却很少,主要针对能力需求生成的框架构建以及生成步骤等,理论比较完善,但缺少定量的分析过程[1-4],本文在这些研究基础上,针对新型武器系统展开作战能力需求生成方法研究,从使命任务出发,研究在这一作战态势下,如何通过定量手段得到武器装备所需的作战能力指标值,重点分析从作战任务到能力指标之间的映射规则,建立符合作战想定的数学模型,从定量角度生成能力需求指标,在此基础上进行能力满足度分析。

1 框架构建

1)对武器系统作战任务分析,需要明确海上武器装备所面临的使命任务,引入元任务,构建其作战任务剖面,进行作战任务分解,最终采用能够实现一定作战目标且相对独立的最小活动单元——元任务序列,描述复杂而宏观的作战任务。

2)武器系统作战能力分析,包括建立作战能力指标体系,对应分析作战任务与作战能力之间的映射匹配关系,根据毁伤目标下的作战任务建立相应的数学模型,明确任务-能力之间的映射关系,生成作战能力指标需求方案[5]。

3)在生成武器系统作战能力需求方案的基础上进行能力需求满足度评估,度量作战能力完成作战任务的程度,以此检验武器系统作战能力需求生成方案的有效性。

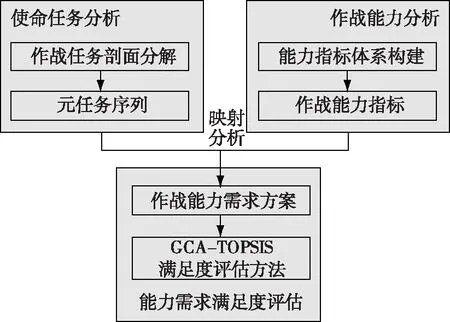
图1 作战能力需求分析框架

2 使命任务分析

欧阳莹之提出的综合微观分析方法[6](Synthetic Micro-analytic Approach, SMA)在对宏观事物进行研究时,可以把整体分解为部分,进行局部的分析,再将局部整合起来,获得宏观的系统认知。

对武器系统进行使命任务分析,目的是分析在未来战场环境下,武器装备所担负的主要作战任务,由于使命任务相对宏观,采用分解的思想,引入元任务概念,对所担负的使命任务进行分解,形成元任务序列来表征使命任务。元任务是作战行动过程中具有原子性事务处理性质的作战任务,这种作战任务是相对固定、相对独立、能够实现一定作战目标的最小任务单元;进行作战任务分解就是将宏观的使命按照特定的原则分解成较低层次、相对明确的元任务清单。

随着武器装备的不断发展,其优越的战技性能,使之在未来战场具有良好的应用前景,可承担防空反导、对海、对陆等多种使命任务,对目标进行打击时,由舰载传感器提供目标信息,本舰作战系统向武器系统发送目标指示,由跟踪传感器自动跟踪目标,跟踪好后将数据传给火控设备,火控设备解算后控制武器进行射击,武器系统控制跟踪传感器获取目标观测信息,进行校射和毁伤评估。经分解后得到的元任务序列如图2所示。

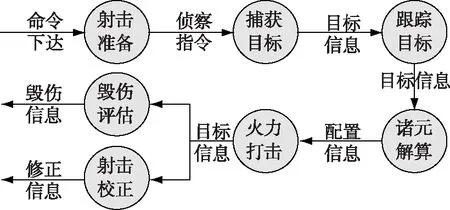
图2 元任务序列图

3 作战能力分析

3.1 能力指标体系的构建

作战能力是武器装备的自身属性,表现为完成具体作战任务所具有的“潜力”。结合传统武器系统,建立新型武器系统的作战能力指标体系,武器系统的作战能力表现在威力、射击精度、反应时间以及射击效能上,采用自上而下的分解方式对每一级的能力指标进行分解,最终形成一个具有递阶结构的能力体系,体系的最底层即是武器装备具体的能力指标[7]。

完成对作战任务与作战能力的逐层分解后,得到武器系统的元任务序列与能力指标体系,这种分解能够帮助作战指挥人员了解使命任务是通过哪些元任务来实现,元任务与能力指标之间具有对应关系,这种对应关系可以明确元任务的执行需要哪些能力作为支撑。武器系统作战能力指标体系及元任务与能力指标间的对应关系如图3所示。

图3 能力指标体系及对应关系

3.2 映射关系分析

得到元任务与能力指标之间的对应关系,对武器系统实现作战能力需求生成便落脚为元任务执行水平到能力指标取值的转换,这种转换即是一种映射[8]。通过作战模拟建立符合作战任务的数学模型,对能力指标的生成过程进行分析,利用军事运筹理论,系统工程理论,作战数模原理等建立数学关系式,生成能力指标的定量需求。采用解析规则描述元任务与能力指标之间的映射规则具有明显的优势,通过建立数学模型模拟作战过程,公式简单明了,便于理清能力指标之间的关系,通过影响因素的变化可分析能力指标的变化趋势,因此通过解析映射关系可实现元任务到能力指标取值的定量映射分析。

武器的速度越高,对目标的毁伤能力越强,随着装备的不断发展,在速度方面得到了很大的提升,如电磁轨道炮、新型火箭弹、鱼水雷等武器装备,设初速为v0,武器装备出口动能E为[9]

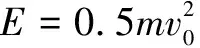
(1)

式中:v0为武器初速;m为弹丸质量。

在作战中要尽可能早地发现并捕获目标,因此最大发现距离与武器系统的有效射程、反应时间、弹丸飞行时间等因素有关,最大发现距离Sd为[10]

Sd=Sr+(tpf+tfr+tsr)×va

(2)

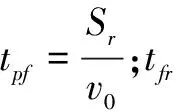
根据战场态势进行作战能力需求生成,若已知目标在一定距离外,可将这段距离近似为最大发现距离,进而反推出武器系统的有效射程。

武器系统对目标的最大跟踪距离St即为

St=Sr+(tpf+tfr)×va

(3)

武器系统的精度指标与射击效能密切相关,根据系统的射击效能指标要求,当系统的两组误差呈最佳匹配关系时,系统精度、目标特性等因素有关的参数可按照下式计算求得[11]

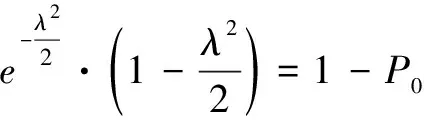
(4)

式中,P0为系统的射击效能指标;λ为综合影响参数,与系统精度、目标特性等因素有关的参数。

火控系统误差σc的计算则与毁伤目标的命中面积,目标的易损性以及武器系统发射的弹丸数有关,因此武器全系统随机误差的均方差σ、系统误差M以及当对目标进行连续射击时,连发散布误差均方差σfs和随动系统误差的均方差σss可按下式进行估算:

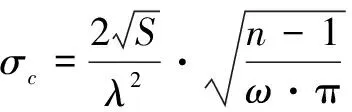
(5)

(6)

(7)

式中，S为目标的命中面积;ω为毁伤目标所需平均命中弹数;n为发射的弹数。σfs为武器系统射击时,弹丸高低散布均方差和方向散布均方差;σss为随动系统高低均方差和方位均方差;Kp为武器系统精度分配因子,0≤Kp≤1。

根据作战任务和所要达到的毁伤效果,武器系统的射速指标np应满足:

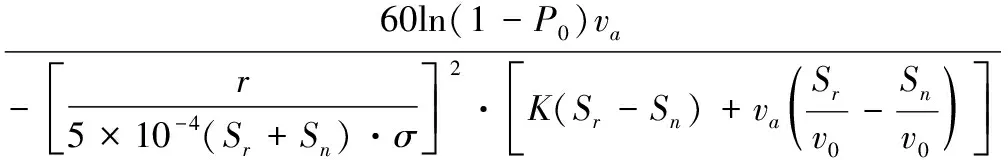
(8)

式中，np为射速,发/min;r为目标域半径;K为目标航路修正系数。

当弹着点对目标圆心的偏差量服从瑞利分布时的单发命中概率p为

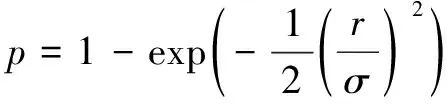
(9)

当每次发射的单发命中概率相同均为p时,对目标的毁伤概率达到P0时所需发射的弹药数为n为

(10)

4 能力需求满足度分析

通过武器系统作战任务与作战能力的映射分析,可以生成能力指标的需求列表。武器系统作战能力的提升离不开其关键技术的支撑,能力建设的目的就是满足作战需要,对武器系统进行能力需求满足度分析,可以确定相关技术是否满足任务能力需求。在灰色关联分析法和理想解法的评估方法的基础上,从贴近度和关联度的角度分析需求满足度,贴近度表示能力指标值与理想值之间的差距,反映了作战能力指标值与理想值之间的关系;关联度表示能力指标无论在理想与现实中都存在一种潜在的关联,即相似性,反映的是能力指标值作为一个整体与理想值之间的关系[12]。

根据能力需求生成过程中建立的能力指标体系,对能力指标进行规范化处理,将能力指标分为效益型与成本型,对其的规范化处理如下。效益型指标的规范化处理函数为

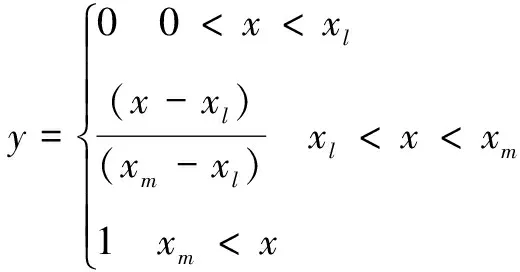
(11)

成本型指标的规范化处理函数为

2.2.4 建立拓扑并进行连通性分析。现已获得单线河流矢量数据，并对该提取结果进行投影变换。建立个人地理数据库和数据集，导入中轴线数据，通过添加拓扑规则完成拓扑新建及拓扑检查。检查无误后新建网络数据集，选取两端点实现提取结果连通性分析。

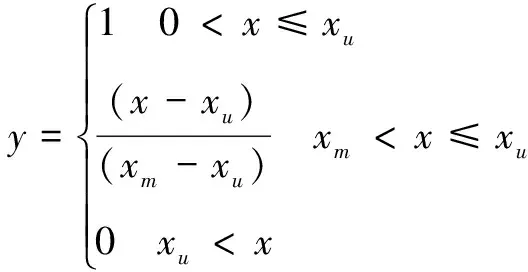
(12)

1)采用层次分析法确定武器系统各能力指标对完成目标任务的不同权重w=(w1,w2,…,wn)。

2)采用改进的TOPSIS求解贴近度,经映射分析后定量得到武器装备完成作战任务的能力指标值,即决策矩阵A=(ai)1×n,结合权重集w生成加权规范矩阵B=(bi)1×n,其中bi=ai×wi;确定加权后的正理想解为B+=(w1,w2,…,wn),负理想解为B-=(0,0,…,0);根据能力指标值到正负理想解的距离d+和d-确定到理想解的相对贴近度C。

(13)

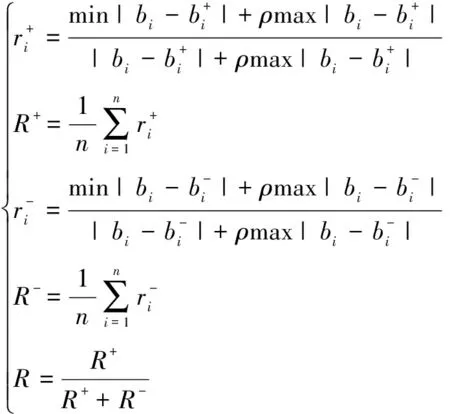
(14)

4)定义能力需求满足程度是贴近度和关联度的结合,S=Cα·Rβ,其中S为能力需求满足程度,α,β∈(0,1),且α+β=1。

5 仿真分析

在武器系统作战能力需求生成中,首先需要判断武器装备对敌方目标的发现距离,假定在距武器装备150 km外有敌方导弹目标以高度为3 km、超声速Ma=2袭来,对于武器装备已知的作战参数如表1所示,根据战场态势分析拦截并毁伤敌方导弹目标所需的作战能力。对于服从正态分布的参数,每一次仿真计算中的取值用符合正态分布的随机数来产生,已知的作战参数如表1、表2所示。

表1 作战参数值

表2 影响参数值

根据武器系统作战过程中的映射关系建模分析,进行作战能指标的需求生成,理想值为对敌目标毁伤效果达到90%,实际值为对敌目标毁伤效果达到60%时对武器系统能力指标的要求,作战能力指标需求值如表3、4所示。

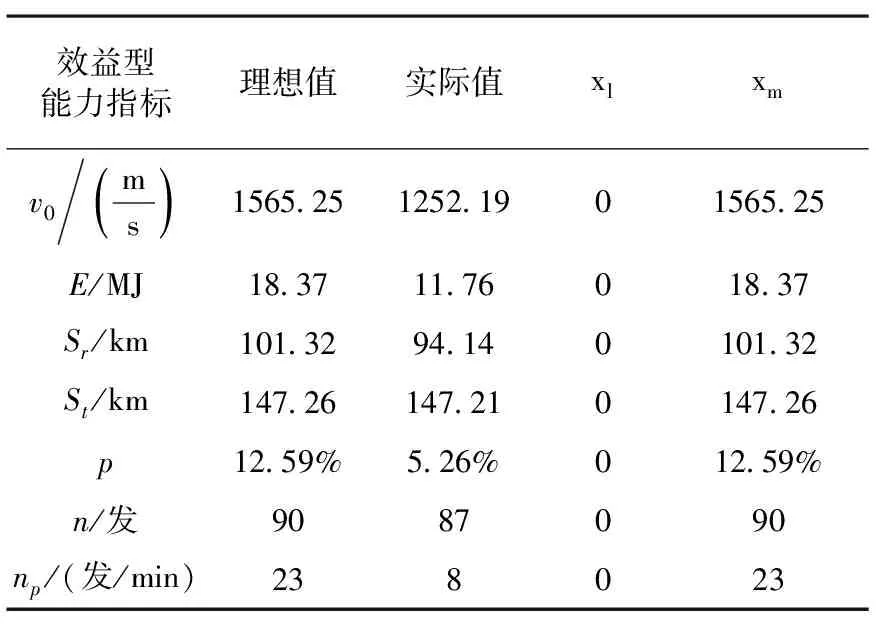
表3 效益型指标值

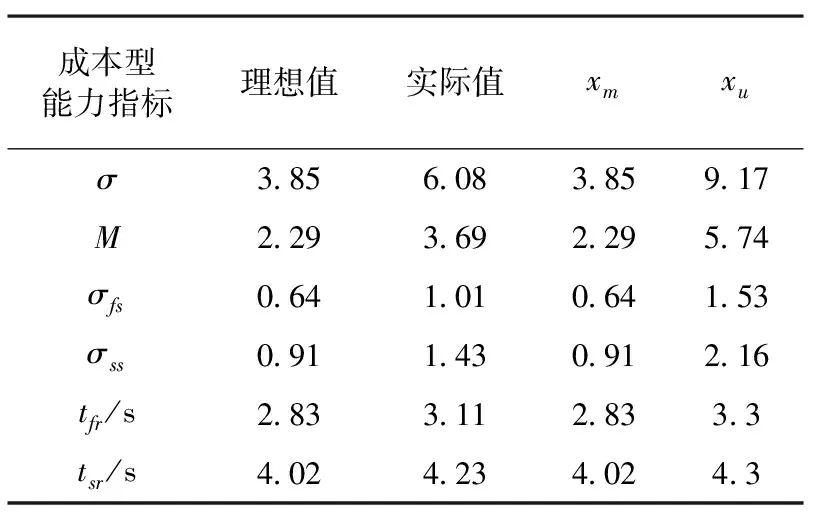
表4 成本型指标值

经映射分析得到在具体作战态势下的武器系统作战能力需求指标值,对指标进行规范化可得决策矩阵A:

A=[0.7999, 0.6402, 0.9291, 0.9997, 0.4178, 0.9667, 0.3478, 0.5808, 0.5942, 0.5843, 0.584, 0.4043, 0.25]。

根据层次分析法得到指标的权重w:

w=[0.2244, 0.1942, 0.0591, 0.0543, 0.0869, 0.0147, 0.0377, 0.0251, 0.0238, 0.0175, 0.0183, 0.1029, 0.1413]。

则加权决策矩阵为:

B=[0.1795, 0.1243, 0.0548, 0.0543, 0.0363, 0.0142, 0.0131, 0.0145, 0.0142, 0.0102, 0.0107, 0.0416, 0.0353]，

B+=[0.2244, 0.1942, 0.0591, 0.0543, 0.0869, 0.0147, 0.0377, 0.0251, 0.0238, 0.0175, 0.0183, 0.1029, 0.1413]，

B-=[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]。

所以由式(14)可得d+=0.0449,d-=0.1795,Cj=0.7999;由式(15)可得这组能力指标对正理想解的灰色关联度为R+=0.7168,对负理想解的灰色关联度为R-=0.8023,所以R=0.4719。因此武器系统完成该作战态势下的能力需求满足度S=Cα·Rβ=C0.5·R0.5=0.5337。

从满足度结果来看,能够较好地满足武器系统对来袭敌导弹目标的拦截需求,表明武器系统完成整个射击任务的作战能力在整个作战能力指标中的重要程度,约占53.37%。按照此方法同理可得：新型武器系统在情报侦察、指挥控制等其他方面作战能力的满足程度,在能力需求的牵引下,充分挖掘武器系统所供与真实作战所需的矛盾程度,依次进行相关能力的建设与发展。由于分析数据源基本来自主观赋值,因此对相关数据采用数学方法进行修正处理,能够较好地控制主观判断带来的差错,使评估结果更加科学可信。

6 结束语

作战能力指标是武器系统需求论证的重要内容,本文提出的基于解析规则下的武器系统作战能力需求生成方法,通过建立武器装备在作战过程中的数学仿真模型,定量生成作战能力指标值,克服了传统定性分析的不足,分析过程清晰直观,生成结果科学可靠,同时采用基于GCA-TOPSIS方法评估了武器系统在毁伤目标条件下的任务满足度,验证了作战能力需求生成指标的可靠性。从总体上讲,该方法通过模型建立、简单可靠,为新型武器装备提升作战能力提供一定的参考。