电磁发射深弹外弹道建模与仿真
2019-03-01陆泽平吴茂林
陆泽平,吴茂林
(海军工程大学,湖北武汉 430000)
现代军事技术不断变革,对于高速、高动能武器的需求不断增加。基于电磁技术发射武器,发射能量控制方便,具有弹丸初速可控、系统反应迅速和射程范围大等优点。电磁发射大口径深弹武器,与火箭深弹相比,可以根据需要方便地控制深弹出管速度,没有燃气冲击,理论上可大幅降低发射时发射装置的振动,减小初始扰动影响,提高射击精度。
最近几年,国内外不少学者对电磁发射武器进行了研究,文献[2]通过分析最大射程角和最大射高,研究了弹形系数、弹丸初速对弹道的影响;文献[3]对电磁发射武器外弹道运动电枢图像及内轨道表面损伤形貌展开分析研究;文献[4]研究了电磁轨道发射装置膛内磁场分布;文献[5]通过仿真给出了电磁轨道炮一定散布范围内的高低概率误差和方向概率误差等。
本文依据建立的电磁发射大口径深弹外弹道模型,针对圆柱平头固定尾翼的弹型,优化设计不同出口速度条件下的外弹道数据,分析出口速度与射程的对应关系;为保证飞行稳定,进一步探究了压心位置、初速误差以及风等因素对弹道参数及飞行稳定性的影响,为初步确定弹体与弹丸结构设计参数提供依据。
1 外弹道模型
深弹在空中飞行的轨迹和姿态,决定了命中目标的准确度,设计合理的飞行弹道是达到最大射程和最佳射击密集度的基础;弹丸的轨迹和姿态除受到气象条件影响外,主要有深弹弹丸的弹形系数和飞离管口瞬间的初始条件决定。
1.1 弹型和坐标选取
基于圆柱平头面固定尾翼的外型,选择同类型深弹的阻力系数-马赫数曲线,并对弹丸的质心运动在如下假设下建立刚体六自由度弹道模型。
1)弹丸是轴对称体;
2)地表为平面,忽略重力加速度随高度的变化(g=9.8 m/s2)方向铅直向下;
3)科氏加速度为零,地球旋转的影响只考虑离心力的部分;
4)气象条件是标准大气模型USSA76;
5)在飞行过程中,弹轴和速度矢量间总存在一个不大的章动角(或攻角)。
根据无控轴对称深弹深弹的特点,选取确定地面坐标系、弹道坐标系和弹轴坐标系三个坐标系。
1.2 六自由度外弹道模型
深弹在空中的运动分为质心运动和围绕中轴线的转动,将质心运动矢量方程向弹道坐标分解,围绕质心运动方程向弹轴坐标分解,质心总动量矩是深弹各质点相对质心动量矩之和,用质心运动规律和质心运动定理确定,转动依靠动量矩定理确定,建立的刚体六自由度深弹外弹道运动轨迹模型如下:
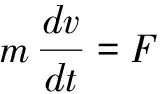
(1)

(2)
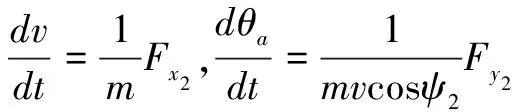
(3)
(4)
(6)

(7)

(8)

(9)

(10)

(11)

(12)
sinδ2=cosψ2sinφ2-sinψ2cosφ2·cos(φa-θa)
(13)
sinδ1=cosφ2sin(φa-θa)/cosδ2
(14)
sinβ=cosψ2sin(φa-θa)/cosδ2
(15)
式中,m为深弹的质量,v为弹速(m/s);θa为速度高低角;ψa为速度方向角;φa为弹轴高低角;φ2为弹轴方位角;δ1为高低攻角;δ2为方向攻角;ωη为绕弹轴坐标系中η的角速度;ωξ为绕弹轴坐标系中ξ的角速度;γ为从弹轴坐标系绕过的角度;x,y,z为地面坐标系坐标;β为弹轴与速度夹角。
2 弹道参数仿真分析
2.1 弹道曲线
深弹射程覆盖范围是通过电磁发射装置调节弹丸初速来实现的,要想获得大的覆盖范围,必须具有较大的速度调节能力。
本文对出口速度分别为50 m/s和200 m/s的弹体进行仿真分析其弹道参数,分别探究低速弹体和高速弹体的飞行情况,并初步确定飞行部分弹丸的参数,包括弹径、长度和弹重。
仿真开始时间为0,当高度z为零时仿真结束,固定射角为45°时,低速和高速时的弹道参数如表1和表2所示。
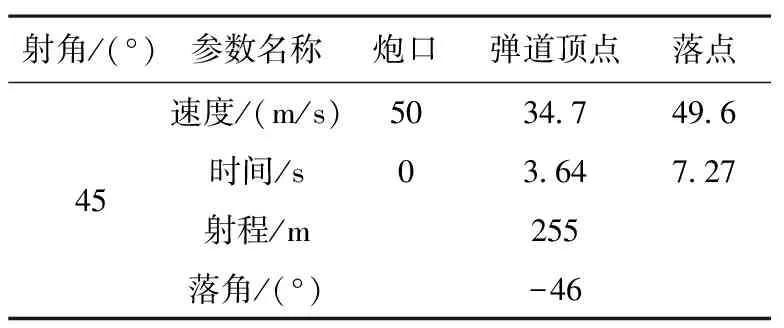
表1 低速仿真结果
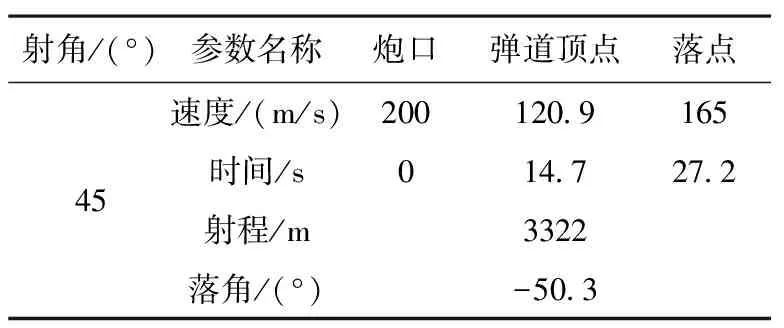
表2 高速仿真结果
2.2 攻角的变化曲线
弹体的运动稳定性和散布情况应重点关注弹轴相对于速度方向的攻角变化规律。攻角较小,意味着弹轴与飞行速度方向基本一致,弹体就可以平稳飞行。若在起始扰动作用后,攻角幅值可以在一个范围内持续收敛,即拥有动态稳定性。攻角幅度收敛越快说明其动态稳定性越好。
考虑到电磁发射出口扰动较小,将初始攻角设为5.7°。弹体初速为50 m/s时,攻角变化如图1所示,其攻角变化周期较长,峰值的整体变化虽有收敛趋势,但第三和第四个峰值依然大于初始攻角。弹体初速为200 m/s时,攻角变化周期短且稳定收敛,如图2所示。
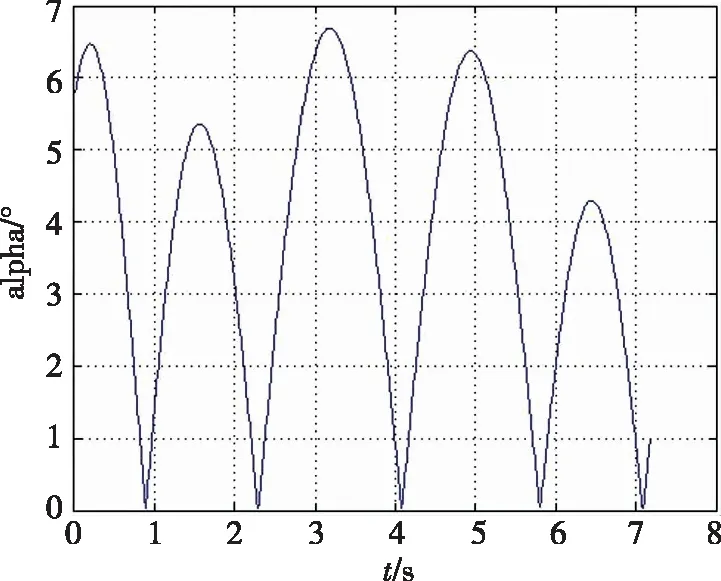
图1 v0=50m/s时攻角变化

图2 v0=200m/s时攻角变化
所以初速越大,攻角收敛性越好,弹体也更稳定。
2.3 最大射程角
在相同的仿真条件下,选用不同的发射角度,分析最大射程时的发射角。
通过初步计算,最大射程角在44°到45°之间.对低速(50 m/s)和高速(200 m/s)分别计算射程,计算结果如表3、4所示。
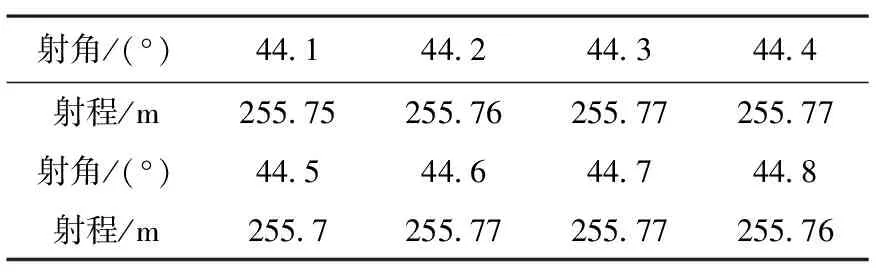
表3 低速(50 m/s)不同射角条件下射程

表4 高速(200 m/s)不同射角条件下射程
由表3得出,低射速出管的弹体,发射角在44.3°到44.7°之间时,射程最大为255.77 m;从表4得出,高射速出管的弹体,射角为43.9°时,射程最大为3365.29 m。
射角在44°到45°之间变化时,射程变化小于1 m射角在最大射程角左右变化时,产生的射程误差相对较小。因此,选择最大射程角不仅保证了射程达到预期,也可以减少误差值。
2.4 初速-射程对应曲线
电磁发射深弹通过控制出口速度调节射程大小,在预定区域打击水下目标,拥有一条出口速度与射程的精确对应曲线尤为重要。
在50 m/s到300 m/s之间,每间隔1 m/s进行一次仿真,测量并记录射程,绘制初速-射程对应曲线图如图3所示。

图3 初速-射程
从图中我们可以得出,当目标射程为500 m时,出口速度为75 m/s;当目标射程为5 000 m时,初速为275 m/s,并且在低射程和高射程可以近似为线性关系。
3 弹体稳定性仿真分析
3.1 初速误差对射程影响
从出口速度与射程对应关系可以看出,在初速为150 m/s的时候,曲线斜率最大,当初速改变时,射程的相应变化量最大。现考察初速变化5%,不同速度状态下引起的射程误差,如表5所示。

表5 初速误差影响
从表5中可以看出,初速变化5%,速度越高引起的射程误差越大,当速度大于250 m/s时,射程误差将大于300 m。要想实现精确打击,必须对初速进行精确控制。
3.2 风对弹道影响
风通过改变弹体相对空气速度的大小和方向来改变空气动力,进而影响弹丸的运动。实际风速、风向随高度和位置变化,为便于修正,我们用求弹道平均值的方法,求得不变的风代替,称之为弹道风。为了研究方便,将风在弹体速度方向和垂直速度方向上分解,得到纵风ωx和横风ωz,纵风主要影响射程,横风主要影响方向。
本文先对纵风和横风对高速弹的修正进行研究。考察初速为200 m/s的弹体,受纵风影响下的射程变化,如表6、7所示。

表6 纵风对高速弹的影响

表7 横风对高速弹的影响
从表6、7可以看出,无论是横风纵风,对于射击精度影响都很大。当风速达到20 m/s时,射程偏差达到百米。所以在大风条件进行射击作业时,要有方向角的修正。
我们继续考察纵风和横风对低速弹的影响。当初速为50 m/s时,风速因素的加入增大了攻角的变化幅度,也影响了其收敛性,如图4所示。
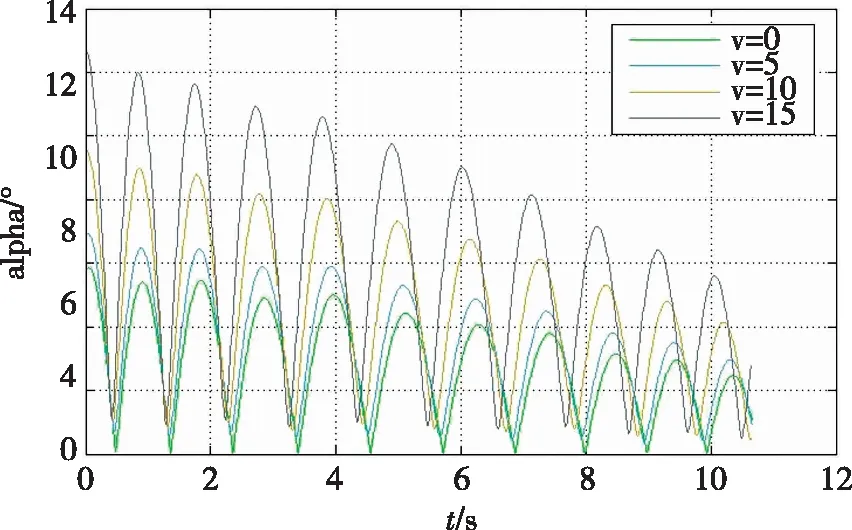
图4 不同风速下攻角变化
风速对出口速度很低的弹体飞行轨道影响很大。为保持水平偏移,可以通过底部排气、底凹等方法弥补。这些方法不仅可以增加射程,也有利于减少风偏。
3.3 压心相对位置对稳定性的影响
压心相对位置(X-C.P.)指空气对弹体表面的作用点与质心在中轴上的距离。正值表示作用点在质心靠近弹头的方向,负值表示作用点在质心远离弹头的方向。这个数值在弹的外形设计中确定,影响着弹体飞行时的稳定性。
我们通过设置不同的弹体外形,分析深弹稳定性变化,获得最佳压心相对位置值。
设模拟深弹出口速度为150 m/s,风速为0,其他仿真条件不变。图5-7反应攻角变化情况。
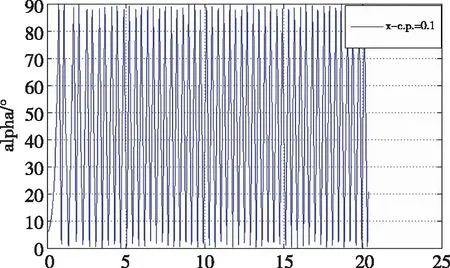
图5 X-C.P.=0.1
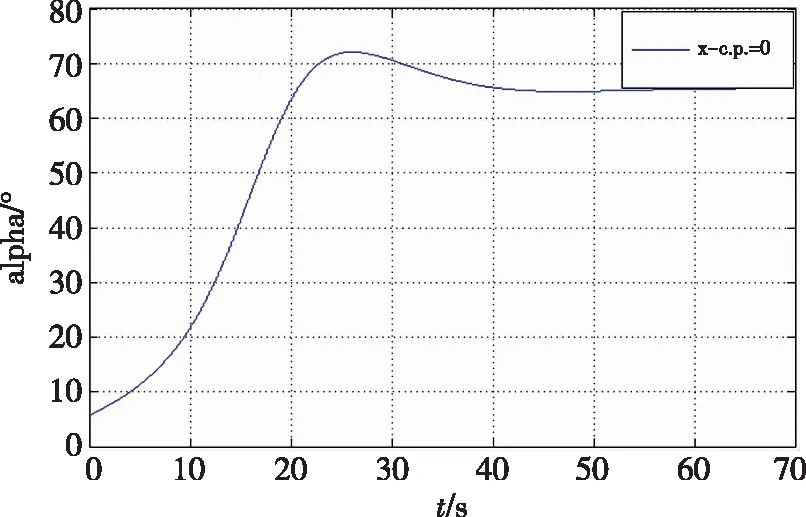
图6 X-C.P.=0
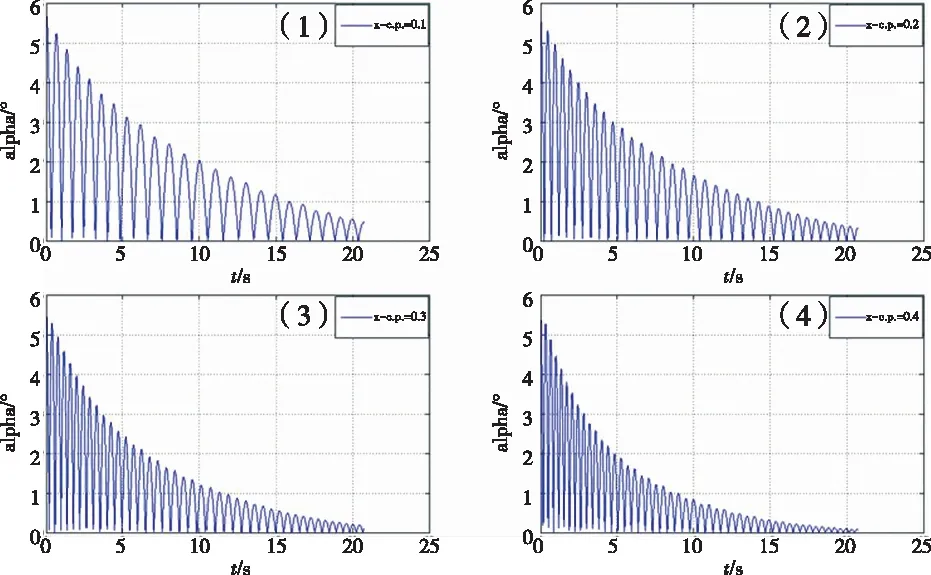
图7 (1)X-C.P.=-0.1;(2)X-C.P.=-0.2;(3)X-C.P.=-0.3;(4)X-C.P.=-0.4
对比不同压心相对位置的攻角变化可以看出, X-C.P.为正值或0时,弹体无法保持稳定性;
当X-C.P.为负值,数值越小,深弹的飞行稳定性调节越快。
X-C.P.数值是由气动外形跟重心决定的,而深弹的整体长度一定,所以这个数值受外形约束。在外形气动设计部分,适当减小X-C.P.的数值,将有利于深弹的飞行稳定性。当深弹的阻心与质心的距离与全长的比值为 10 % ~ 15 %,就能保证其具有良好的静态稳定性。
4 结束语
本文针对电磁发射的大口径弹丸,建立了其六自由度运动方程和外弹道模型,通过四阶龙格-库塔法解算弹道方程,进行外弹道设计仿真,确定了最大射程角,得到初速与射程对应曲线,利用攻角的变化图像,分析了初速误差、风速和压心相对位置对于深弹发射稳定性的影响。
仿真结果表明,设计的电磁发射大口径深弹能满足其射程要求,无论低速段还是高速段都可以保持良好的稳定性;风和初速误差造成的偏移不容忽视。特别是小射程低速发射时,风对于深弹在空中的姿态影响比较大;在外形气动设计部分,适当较小X-C.P.的数值,将有利于深弹的飞行稳定性。当深弹的阻心与质心的距离与全长的比值为 10 % ~ 15 %,能保证其具有良好的静态稳定性。本文对外弹道的仿真与分析为进一步优化设计奠定了基础。
