Solution of the finite slab criticality problem using an alternative phase function with the second kind of Chebyshev polynomials

Hakan Öztürk ·Ökkeş Ege

Abstract The critical size of a finite homogenous slab is investigated for one-speed neutrons using the alternative phase function(AG,Anlı-Güngo¨r)in place of the scattering function of the transport equation.First of all,the neutron angular flux expanded in terms of the Chebyshev polynomials of second kind(UNapproximation)together with the AG phase function is applied to the transport equation to obtain a criticality condition for the system.Then,using various values of the scattering parameters,the numerical results for the critical half-thickness of the slab are calculated and they are tabulated in the tables together with the ones obtained from the conventional spherical harmonic(PN)method for comparison.They can be said to be in good accordance with each other.

Keywords Criticality problem ·UNmethod·Neutron transport equation·Alternative phase function

1 Introduction

The particle transport equation,which was first developed by Boltzmann for the kinetic theory of gases,is based on the conservation of the neutrons in a reactor system.The radiative transfer of stellar and planetary atmosphere and light scattering phenomenon are also related to the transport concept.Therefore,the description of the behavior of the neutrons in a reactor has a great importance for the first calculation and thus the construction and the operation of the reactor uneventfully.The number of fission neutrons is wanted to be constant in all types of reactors in order to obtain constant power and to control it safely.This situation of the reactor is de fined as to be critical,and the criticality of a fission system is one of the most important problems in neutron transport theory.Therefore,the critical size of a reactor can be said to be decided after the investigation of the criticality problem related to the system under consideration.

As well known,the transport equation is an integrodifferential equation,and thus,it is not easy to solve it analytically.The discrete ordinates(SN)and polynomial expansion-based techniques are accepted to be the most common and powerful ones among the methods developed for the solution of the transport equation[1-4].In about all methods,either the derivative of the neutron angular flux or the neutron scattering function presented in the integral part of the transport equation is treated by some approximations to simplify the solution of the equation.In some instances,using an approximated scattering function in the transport equation can be suf ficient depending on the scope of the problem under consideration.However,these approximations can take the problems,and thus,the solutions are more or less away from the real situations.Since the scattering cross sections vary with the scattering angle incredibly,various dif ficulties occur when the scattering function is represented in terms of any polynomials.Therefore,instead of using approximate expressions,if an exact scattering model is used in place of the scattering function,one could obtain more realistic results representing the system better[1,2].

Henyey and Greenstein[5]had first developed an exact scattering function called the Henyey-Greenstein(HG)formula to verify the existence of the diffuse interstellar radiation.However,they did not explain physically in their paper why they used such a function in the radiative transport equation.Later in the following studies such as biomedical applications,signi ficant discrepancies have been reported about using the Henyey-Greenstein formula[5-8].

In this paper,an alternative scattering function(Anlı-Güngo¨r,AG)which was applied successfully to the criticality problem in neutron transport theory using Legendre and the Chebyshev polynomials of first kind is preferred[9-11].However,instead of using the first kind of Chebyshev polynomials,the second kind of Chebyshev polynomials approximation(UNmethod)is preferred to serve as an alternative solution method to the literature.This method has been successfully applied to the solutions of the problems of the transport equation in nearly a decade[13,15].Therefore,this study can be thought of as the extension of the study previously carried out by Öztürk[11].In the solution algorithm,the neutron angular flux is first expanded in terms of the Chebyshev polynomials of second kind;then,the AG phase function is inserted into the transport equation in place of the scattering function.At the end,applying the UNmethod to the resultant equation following the moment equations,a general expression for the criticality condition is obtained for one-speed neutrons.Then,the critical half-thicknesses of the slab are calculated using various scattering and collision parameters in the criticality condition.The numerical results are obtained with an increasing order of N=1-9,and they are listed in Tables 1,2,3 and 4.Finally,a comparison table including the results obtained from the present method and the results obtained from the conventional PNmethod is given.

2 UNmethod with AG phase function

The stationary transport equation for one energy group neutrons in a source free medium can be written as,

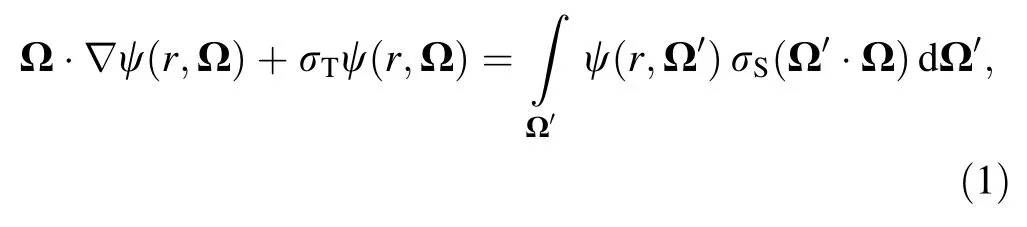
where Ω′and Ω are the unit vectors along the neutron velocity before and after a scattering collision,respectively.c= σS/σTis the cross-sectional parameter known as the number of secondary neutrons per collision and σTis the total macroscopic cross section.ψ(r,Ω)is the neutron angular flux at position r traveling in direction Ω,and σS（Ω ·Ω′）is the scattering function[1-3].

Up to now,an appropriate scattering function representing the probabilities of the neutron interactions is foundto be enough for the solutions of the problems in neutron transport theory because of its mathematical applicability.Although using an approximate scattering function isusually accepted to be successful in many of the studies,the direct form of a scattering function like Henyey-Greenstein could be fascinating both in solution algorithm and in calculation of numerical results.On the other hand,the Henyey-Greenstein phase function is reported to be unsuccessful in some of the studies about radiative transfer[5-7].Therefore,Anlı et al.[9,12]constituted a new scattering kernel,i.e.,an AG phase function similar to Henyey-Greenstein formula and they first applied it to calculate the eigenvalue spectrum in the one-dimensional slab geometry transport equation.In some recent studies,the AG phase function has been applied to diffusion equation and criticality problems in the transport theory using Legendre polynomials(PNmethod)and Chebyshev polynomials of first kinds(TNmethod)[10,11].

Table 1 Numerical results for the critical half-thickness as calculated by increasing orders of UNapproximation for c=1.01 and selected values of t

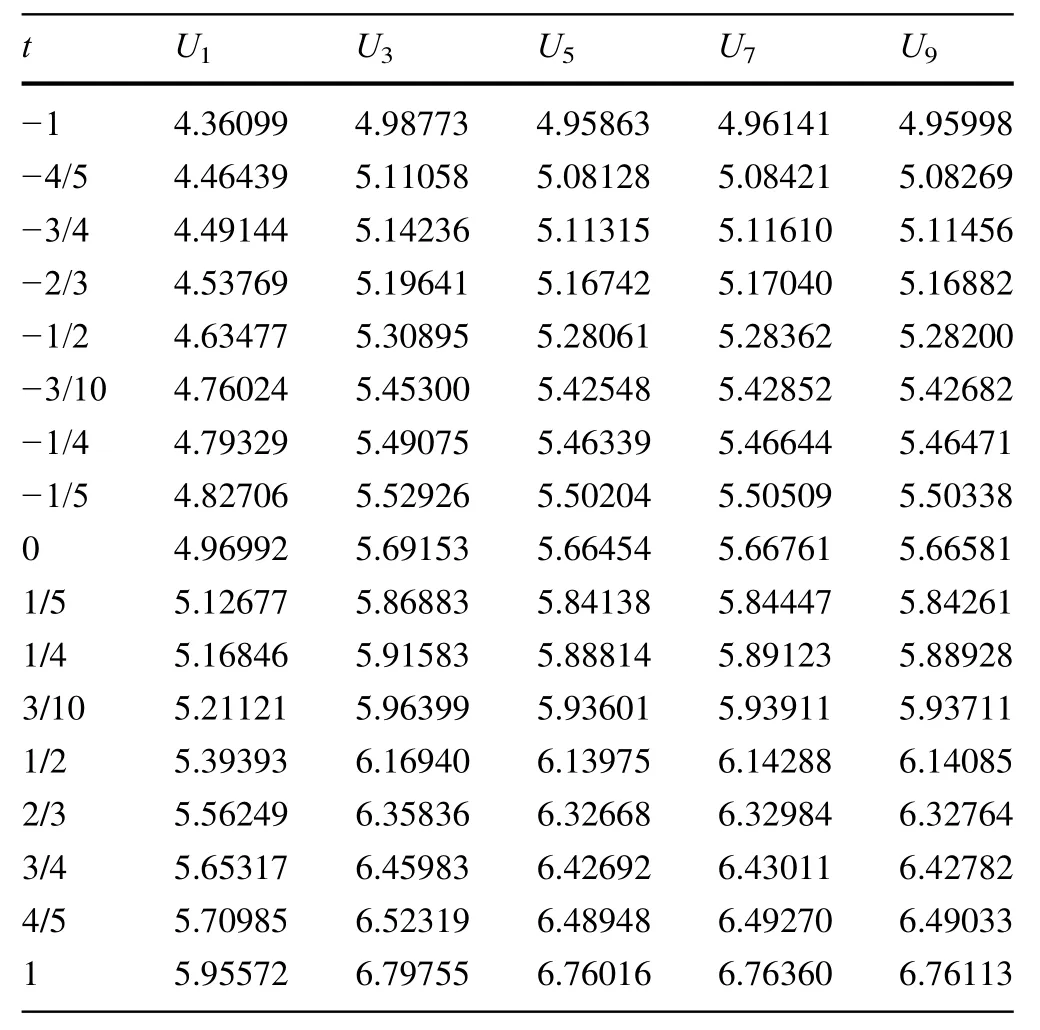
Table 2 Numerical results for the critical half-thickness as calculated by increasing orders of UNapproximation for c=1.02 and selected values of t

Table 3 Numerical results for the critical half-thickness as calculated by increasing orders of UNapproximation for c=1.20 and selected values of t

Table 4 Numerical results for the critical half-thickness as calculated by increasing orders of UNapproximation for c=2.00 and selected values of t

In this work,other than the previous studies about criticality calculations with de fined scattering functions,the Chebyshev polynomials of second kind are preferred for use in the series expansion of the neutron angular flux.The AG phase function is used as the scattering function in the transport equation,and the critical half-thicknesses of the slab for one-speed neutrons are calculated for various values of the scattering parameters.Here,the detailed information about the PNmethod with the AG phase function does not needed to be given since it was mentioned in the previous work by the author[10,11].

The AG phase function,which is first used by Anlı et al.[9]in the determination of the eigenvalue spectrum,is then expressed as the scattering function,σS（Ω ·Ω′）,in neutron transport equation,i.e.,Eq.(1),

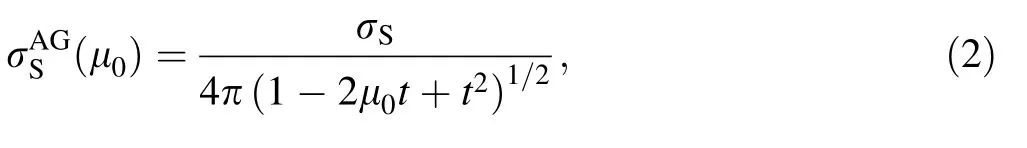
where σSis any nonnegative coef ficient,t is the parameter representing all kinds of scattering(forward,backward and anisotropic)and it is de fined in the range of-1≤t≤1,and μ0= Ω ·Ω′is the cosine of the scattering angle[5,9],

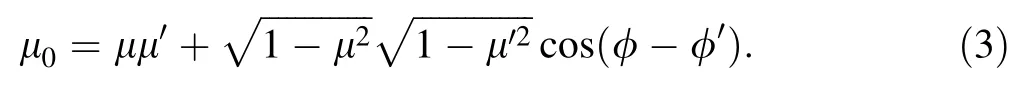
The neutron angular flux is used as in Ref.[13],

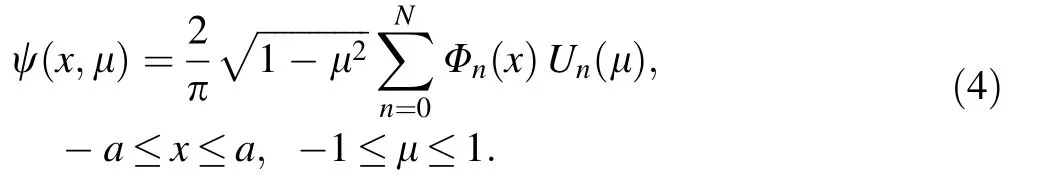
When Eq.(2)is inserted on the right-hand side of Eq.(1),the one-dimensional steady-state transport equation can be written as,

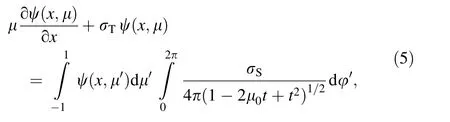
with the free space boundary and symmetry conditions:

The slab is assumed to be homogeneous expanding from x=−a to x=a.The integrand on the right-hand side of Eq.(5)over dφ′can be obtained using the addition theorem of the Legendre polynomials[9],

Then,Eq.(5)can be rearranged using Eq.(7),

A dimensionless space variable,such that σTx/ν→ x is de fined in order to simplify the derivation of the equations and ν,is the eigenvalue.

In the application procedure of the method, first the neutron angular flux,ψ（x，μ）,given in Eq.(4)is replaced in Eq.(8),and then,the resultant equation is integrated over μ ∈ (−1,1)after multiplying it by Um(μ).The orthogonality and the recurrence relations of the Chebyshev polynomials of second kind are used during this procedure[13-15],

By following the steps mentioned above,a general expression for the UNmoments of the angular flux could not be reached in this study.However,individual expressions for n=0,1,2,…,9 are obtained and they are

where Φ−1(x)=0.A well-known solution[1],

is customarily used in Eqs.(11)in order to obtain analytic expressions of all An(ν)'s as follows,

where A−1(ν,t)=0 and A0(ν,t)=1.Equations(13)can also be written in a matrix form for an alternative solution algorithm,

where M(ν,t)is(N+1)× (N+1)coef ficient matrix and A(ν,t)=[A0,A1,…,AN]T.It is possible to obtain non-trivial solutions for the discrete eigenvalues by equating the determinant of the coef ficient matrix to zero,i.e.,det[M(ν,t)]=0.

As well known in the PNapproximation,the contribution of the(N+1)th term to the neutron flux could be accepted as negligible.In addition,the Legendre and Chebyshev polynomials are the members of the Jacobi polynomials.Then by following the same procedure derived for the PNapproximation,the discrete and continuumν eigenvalues can be obtained by setting AN+1(ν,t)=0 for various values of c and t.Brief information about the pro files of the eigenvalues can be given as follows:All roots of AN+1(ν)=0 are identical with the roots of UN+1(ν)=0 in the case of c=0 and all values of t.When c=1,one pair of the roots is±∞i and the others are real lying in the interval[−1,1].When 0＜c＜1,all roots are real and one pair of them is usually greater than 1.Finally when c＞1,one pair of the roots is purely imaginary and the others are real[9,19].As an example for U1approximation,two linear algebraic equations,i.e.,Equation(13a)for n=0 and Eq.(13b)for n=1,are obtained and an analytic expression for the eigenvalues can easily be derived by setting A2(ν,t)=0 in Eqs.(13a)and(13b),

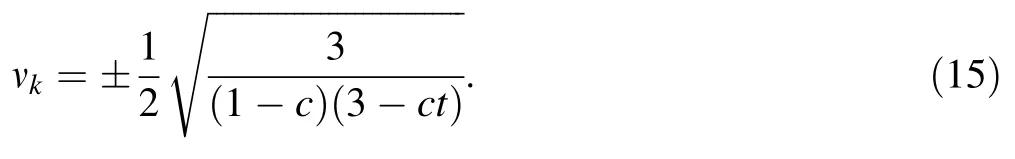
In other words,the same eigenvalues can be obtained using Eq.(14)by deriving a 2×2 matrix equation and then equating the determinant of the coef ficient matrix to zero.

Therefore,the general solution of the flux moments for odd numbers of N can be written with so computed discrete eigenvalues νkfor k=1,…,N+1,

where An(−ν,t)=(−1)nAn(ν,t)and αk's are the coef ficients which can be determined from the physical boundary conditions of the system.The general solution Eq.(16)is constituted as the summation of all eigenvectors corresponding to each eigenvalues.

3 Boundary conditions and the critical system

The study of calculation of the eigenvalues of the problem representing the system under consideration can be said to be equivalent to find the critical size of that system.The values of the number of secondary neutrons per collision are very important to operate the reactor safely and decide whether it is critical or not.In a reactor,for each absorption collision the reactor cannot be said to be critical when fewer neutrons are emitted than absorbed(c＜1).However,a reactor may be subcritical or critical for a slab of finite thickness with c＞1[3].

The angular neutron flux is continuous across material region boundaries except for the direction μ=0 in slab geometries.Any finite sum of the Legendre polynomials is continuous over the range−1≤μ≤1 and,therefore,continuous at μ=0.Then,the PNapproximation in slab geometries is a rather poor representation of the angular flux near material boundaries.Although the Mark and Marshak boundary conditions are the most commonly used ones for the criticality problems,the Marshak boundary condition which is based on the condition of zero incoming current at the vacuum boundary is somewhat more accurate than the Mark condition,at least for small N[3,16].

Because of the reasons mentioned above,for the criticality of the slab,the Marshak boundary condition for UNapproximation of odd order can be written as,

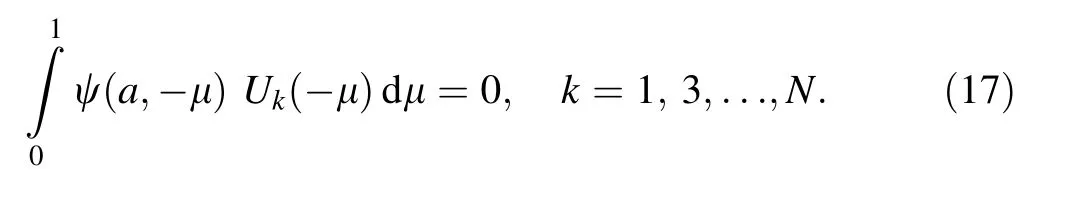
In the application procedure of the boundary condition,fi rst the neutron flux in Eq.(16)is replaced in Eq.(4),and then,the resulting equation is inserted into Eq.(17)with the parity relation of the Chebyshev polynomials of second kind Uk(−μ)=(−1)kUk(μ),

where In,kis

and

Equation(18)is referred to as the criticality condition and it can also be written in a matrix form,

where βkis the column vector comprising elements ofis the coef ficient matrix with(N+1)/2×(N+1)/2 elements.Equation(18)or(21)can be solved for a non-trivial solution when the coef ficients βk's are nonzero or the determinant of the coef ficient matrix is zero,i.e.,det=0.Since the eigenvalues were already calculated from Eq.(15),as final application by letting N=1 in Eq.(18)or Eq.(21),an analytic solutionfor the critical half-thickness of the slab can easily be obtained for U1approximation,

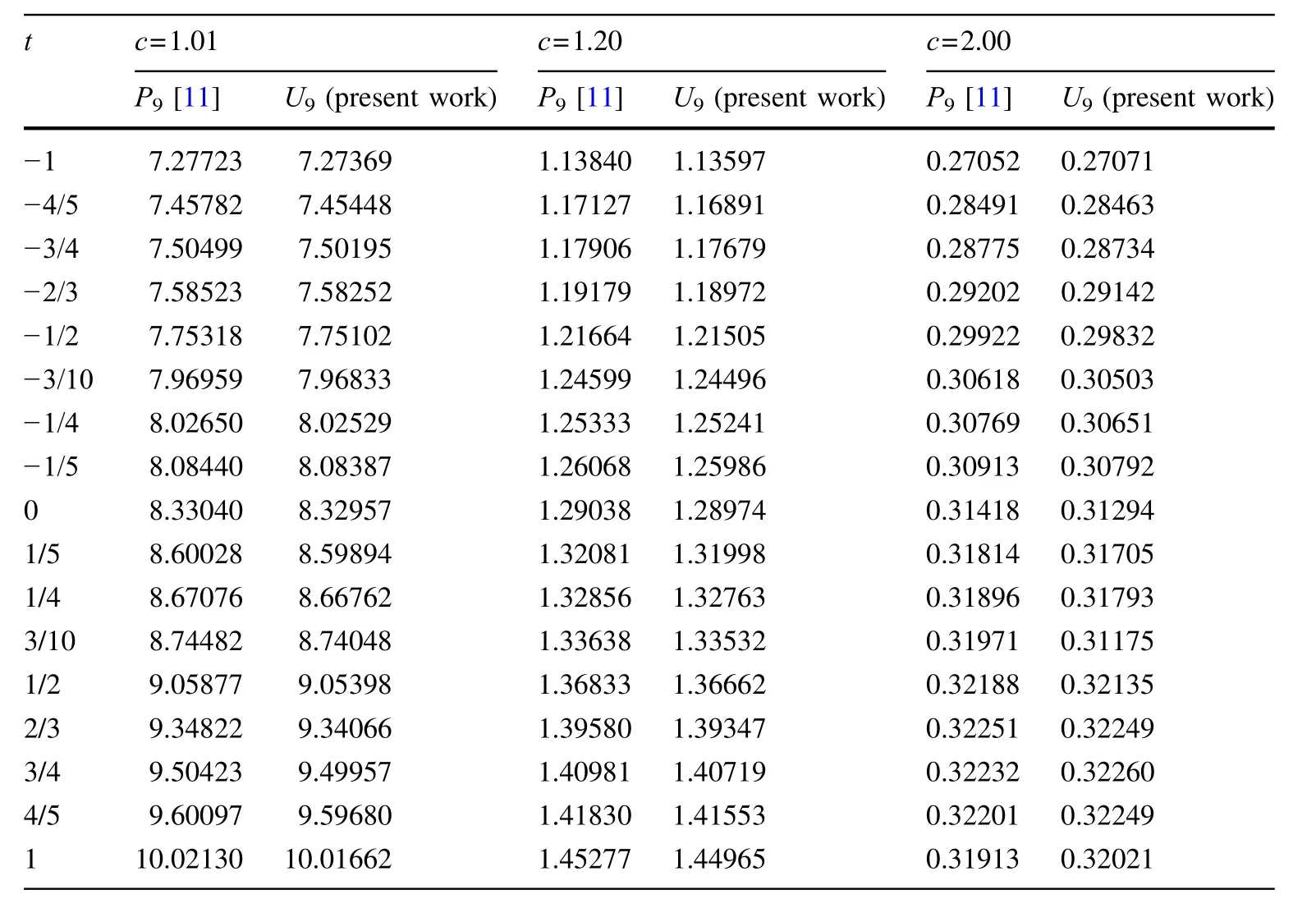
Table 5 Critical halfthicknesses for c=1.01,1.20 and 2.00 and selected values of t as compared by P9and U9 approximations

4 Numerical results

An application of the Chebyshev polynomials expansion(UNapproximation)is done for the critical slab problem for one-speed neutrons in a uniform homogeneous medium.In the method,the Chebyshev polynomials of second kind are used in the angular part of the neutron flux as it has been successfully applied before[13,15].Contrary to previous approximation scattering functions,in order to get closer to accurate solution of the transport equation,the AG phase function is used.Various values of c and t are used in Eq.(13)or(14)to compute the discrete eigenvalues by setting AN+1(ν)=0.An analytic expression of the eigenvalues for U1approximation is obtained and it is given in Eq.(15).Various orders of the UNapproximation with the AG phase function are applied to Eq.(18)or(21),and the numerical results for the critical half-thickness of the slab are tabulated in Tables 1,2,3 and 4.A final table,i.e.,Table 5,has been needed to compare the results obtained from the present method with the ones already obtained from the conventional PNmethod in a previous study[11].The Marshak boundary condition is used during the application of the criticality condition to the problem since it is accepted as to be more valid than the Mark for small N[3,16].All calculations are carried out by means of the Maple software,and the total macroscopic cross section is taken as to be its normalized value,σT=1 cm−1.

In Tables 1,2,3 and 4,the critical half-thicknesses of the slab are listed for c=1.01,1.02,1.20 and 2.00 and t is selected with increasing order from−1 to 1.One can easily test that the t=0 case corresponds to isotropic scattering[9,13,15].In other words,by replacing the case of t=0 in Eqs.(15-18)one would obtain the equations necessary for calculating the eigenvalues and the critical half-thicknesses using the UNmethod in slab geometry for isotropic scattering[13,15].

It can be seen from the tables that in many cases,the critical half-thickness of the slab increases,while t is increasing and c is decreasing.It was reported that the critical thickness of the slab can behave non-monotonic when neutrons tend to propagate in the forward direction.This is observed as first an increasing trend and then a decreasing trend with increasing forward anisotropy parameter according to the choice of the c.This behavior of the critical thickness is referred to as non-monotonic and it is observed in this study for t approaching to 1 and c=2,especially in the case of higher-order approximations with N＞5.That means the same non-monotonic behavior of the critical thickness as reported before[17,18]appears when the neutrons scatter in the forward peaked directions.This circumstance is given in Tables 4 and 5 by examining the values with t＞¼.However,since the criticality calculations are important especially for c near to 1,this anomaly for the AG phase function can be thought as negligible.It can be seen from these tables that this non-monotonic behavior has occurred when c=2.00(away from 1)and higher-order approximation is used(N=9)which is pointed to as the advantage of the Marshak boundary condition against the Mark[3].More discrepancies about the behavior of the critical thickness are reported as to be seen when using Henyey-Greenstein phase function[11].

5 Conclusion

In this paper,the critical thickness of one-speed neutrons in a finite homogeneous slab is studied using UNapproximation which is applied successfully in preceding studies[13,15].As a second important application of this study,the AG phase function is chosen as the scattering kernel of the transport equation.The critical half-thicknesses of the slab are calculated numerically using increasing orders of the UNapproximation up to N=9 for both positive and negative values of the parameter t.While the positive values of t represent the forward peaked scattering of the neutrons,the negative values of it represent the backward peaked scattering of the neutrons.These are physically possible situations presented in a reactor.When a neutron interacts with a particle having a mass approximately equal to the mass of the interacting neutron,such as a hydrogen nucleus in a moderator,this interaction has a probability to end with a forward scattering.In a similar way,when a neutron interacts with a particle having a mass of greater than the mass of the interacting neutron,such as an oxygen nucleus in a moderator,a nucleus in reactor material or a daughter nucleus emitted from a fission reaction,this interaction has a probability to end with a backward scattering[9].Therefore,this study can be evaluated as the calculation of the critical halfthickness of the slab for forward and backward scattering since both the positive and negative values of t are given in Tables 1,2,3,4 and 5.

In summary,one can easily assert from the derivation of the equations and the results already obtained here that the AG phase function is seen to be convenient for the solution of the problems in transport theory.Furthermore,the AG phase function with its easily applicable derivation can also be suf ficient for other problems containing a phase function in particle or photon transport and in science and engineering.