基于Retinex算法的亮度分层图像增强算法

李忠海 宋笑宇 陈灿灿 王崇瑶

（沈阳航空航天大学自动化学院，沈阳，110136）

引 言

在天气、光线等不良条件下，采集到的彩色图像亮度和对比度都比较低，为了增强低照度彩色图像的整体亮度，使图像中物体的细节信息更加清晰，并使其具有良好的视觉效果，研究高质量的图像增强算法受到了国内外很多学者的关注，成为图像处理领域的热点问题。

Retinex理论由Land首次提出，又称为色彩恒常性理论，在图像增强应用中较为广泛[1]。近年来在Retinex算法理论的基础上，国内外学者提出了很多改进的Retinex算法。但是大量实验结果表明，Ret⁃inex理论依然存在“光晕伪影”、图像过增强和算法运算效率低等缺陷[2]。

低照度彩色图像增强的关键是解决在不同照明条件下的图像增强问题。Jang等提出了在光照和物体对比度边缘条件下的自适应权重多尺度Retinex算法，该算法能够获得颜色恒常性和良好的图像动态范围，但增强后的图像会出现过增强现象[3]。Kwon等提出了基于亮度函数的亮度自适应转换图像增强算法，该算法使用构造的亮度函数对图像进行增强，能够使增强后的图像具有良好的对比度和饱和度，但对于亮度较低的低照度图像，增强效果不明显[4]。Lu等提出了使用加权引导三角滤波和人造光校正的水下图像增强算法，使用加权引导三角滤波可以有效保持边缘、减少程序运行时间，但增强后的图像含有大量的噪声[5]。Park等提出了一种基于Retinex模型的微光图像复原方法，该方法具有更好的恢复效果，且没有噪声放大、边缘晕环效应等非自然干扰[6]。常戬等提出了一种基于图像融合技术的Retinex图像增强算法，该算法能有效去除光晕现象、改善图像泛灰的不足[7]。

为了进一步使Retinex算法具有更优的图像增强效果，能更好地保留图像中物体细节信息，本文针对目前Retinex算法存在的不足，提出了一种基于引导滤波的亮度分层Retinex图像增强算法，并在MATLAB实验平台对算法进行了实验验证。

1 Retinex基本理论

在Retinex算法模型中，为了消除入射分量的影响从而得到物体的反射分量，同时为了简化模型的计算使其方便求解，通常对Retinex模型进行对数转换。基于中心环绕的Retinex方法[8]，实际上就是用低通滤波器估计入射图像分量，然后从原图像中去除入射分量进而求得物体的反射分量。

单尺度Retinex(Single scale Retinex,SSR)算法理论公式如下

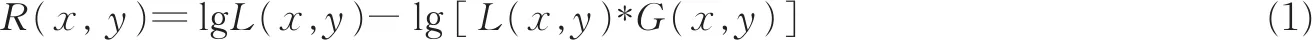
式中：*代表卷积运算；G(x,y)为低通滤波函数，用来估计入射图像分量。

多尺度Retinex(Multi scale Retinex,MSR)理论数学模型为

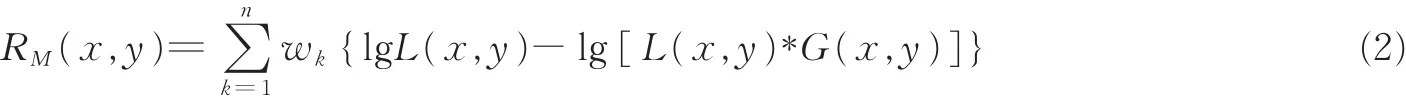
式中：RM(x,y)为反射分量；n为尺度数目；wk表示第k个尺度所对应的权重，并且要满足SSR算法的运算结果进行线性加权求平均值就是MSR算法，且w1=w2=w3=1/3。

2 本文算法

2.1 算法流程

本文算法的整体流程为：将待增强的彩色图像在HSI空间采用引导滤波对亮度图像进行滤波操作，并且提取亮度图像的细节层图像，然后使用亮度图像减细节层图像，最后得到基本层图像。采用一种全新的方法将增强后的细节层图像和基本层图像进行重构得到增强后的亮度图像，在RGB色彩空间对图像进行颜色恢复得到最终的增强图像[9]。算法流程如图1所示。

2.2 亮度图像分层处理

图像引导滤波是一种线性滤波，是由引导图像I，和输入图像p以及输出图像q组成。引导图像I与滤波输出满足局部线性的假设，局部线性模型为[10]

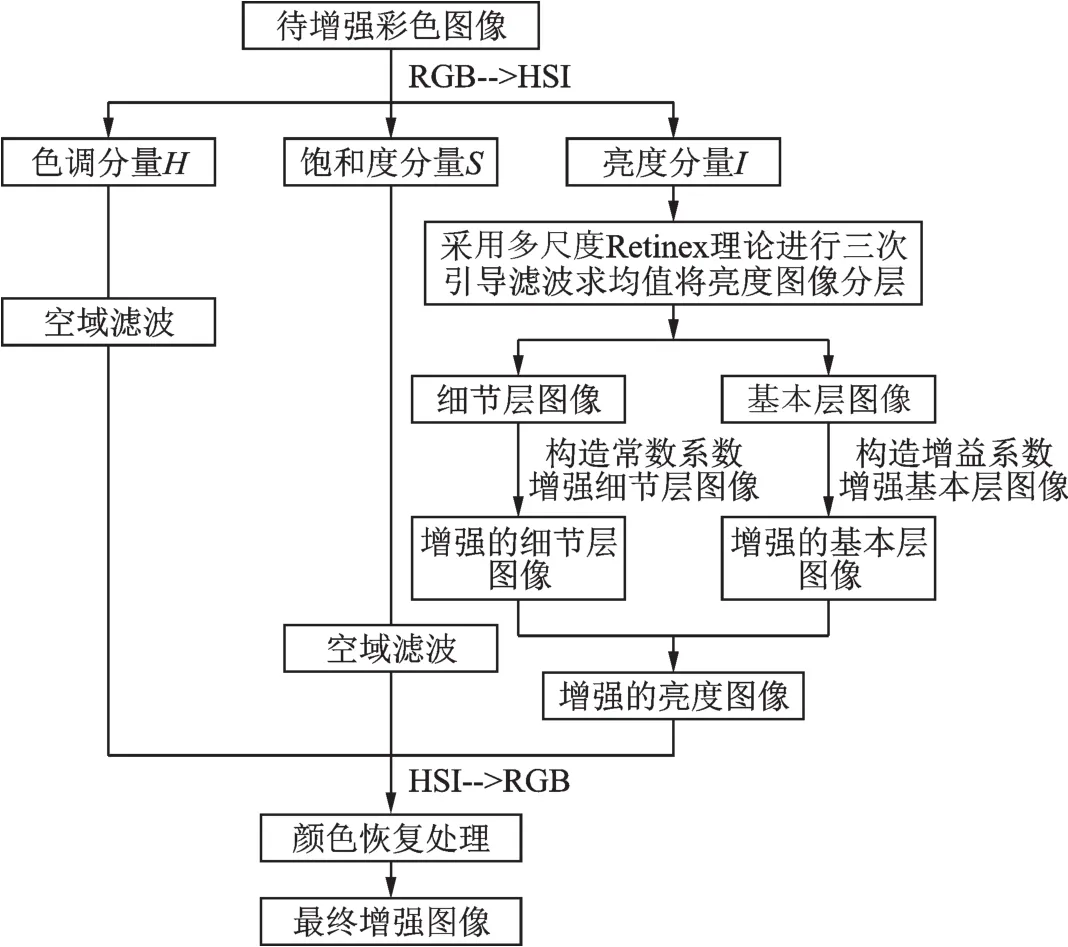
图1 本文算法流程Fig.1 Flowchart of the proposed algorithm

式中：在局部窗wk中，ak，bk为线性系数；i为像素索引；wk为大小为r的局部方形窗口。

ak，bk的表达式为

式中：ε为正则因子，它可以避免ak过大，μk和σk2为位于wk局部窗内I的均值和方差；Nwk为wk窗口中像素数量；-pk为位于wk局部窗口中p的均值。

本文中令引导图像I和输入图像p相同，则式(4)可改写为

式(5)可改写为

从式(6，7)中可以看出ε的取值可以影响ak，bk的大小。为了获得引导滤波函数，对qi在整幅图像上求均值为

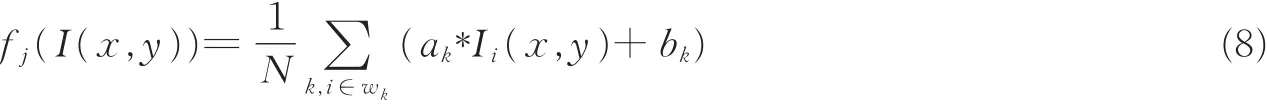
式中：N为图像总的像素数；j为引导滤波的次数。

MSR算法模型对大、中、小3种不同尺度下SSR的运算结果进行综合，从而能够充分地融合不同尺度的优点，使得多尺度Retinex算法的反射分量能够包含更多的图像细节并且能较好地反映动态范围压缩能力。本文借鉴多尺度Retinex算法理论，根据引导滤波中尺度参数取大、中、小3个不同数值进行3次引导滤波求均值来提取亮度图像的细节图像。

图像细节增强的能力是由滤波窗口r和参数ε这两个参数的取值决定。在利用引导滤波核函数对亮度图像进行滤波时，可以根据图像大小来确定滤波窗口r，一般设置大、中、小3个尺度，若预滤波图像的尺寸为m×n，根据实验结果，总结得出r的取值范围由图像自身尺寸大小决定，小尺度r的取值范围为[1,rmin]，中尺度r的取值范围为[rmin,rmid]，大尺度r的取值范围为[rmid,rmax]，[]表示向下取整。其中rmin，rmid，rmax表示为

本文称引导滤波中ε为平滑增益参数，也为引导滤波的尺度参数。由于该增益为全局参数，而且需要事先人为设定[11]。在使用引导滤波算法对亮度图像进行滤波处理时，会因ε的取值不同而对细节图像造成较大影响，导致细节图像的巨大差异。当ε较小时，细节图像会显现的非常平滑，细节表现的不突出；当ε较大时，图像细节表现过于明显。因此本文在求取亮度图像的细节图像时借鉴多尺度Retinex算法理论，ε会取大、中、小3个尺度。

采用式(8)构造的引导滤波函数对亮度图像进行滤波处理，以获得亮度图像的细节图像，细节图像的表达式为

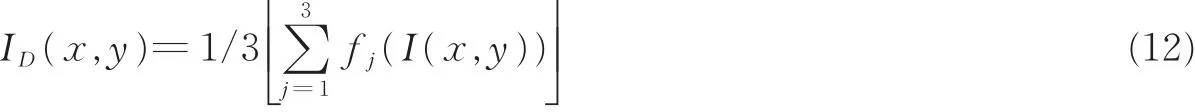
式中：I(x,y)代表亮度图像；ID(x,y)代表细节图像，它是由亮度图像经过3次不同程度的引导滤波后求均值得到的。

当细节图像从亮度图像分出来以后，用亮度图像减去细节图像就可以得到基本图像，基本图像的表达式为

式中IB(x,y)代表基本图像，它是由亮度图像减掉细节图像得到的。

图像的细节是高频信号，它仅仅包含了亮度图像的微弱能量，亮度图像的大部分能量依然存在于基本图像中，因此为了提高图像亮度就要从基本图像着手进行处理。

在本文中，用参数Δφ来表示基本图像的灰度差值，其表达式为

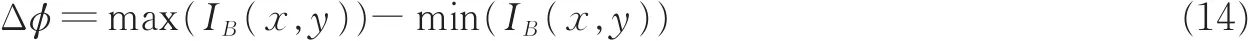
参数Δφ不仅代表基本图像的最大灰度值max(IB(x,y))和最小灰度值min(IB(x,y))之间的差值，也代表待增强图像的最大灰度差值，它是待增强图像动态范围的最基本的特征。

接下来用Δφ参数进行增益系数的计算：用Δφ值构造一个新的λg值来调整基本图像的能量，λg的表达式为

对于每一个计算出的Δφ值，λg都会有特定的增益值，参数ηc是一个预设值，它的设定是为了改变λg值。通常ηc的取值范围为[5,300]，它取决于Δφ的选择和视觉观察。

2.3 亮度图像重构

在基本图像的灰度等级重新排列和细节图像的细节增强以后，把经过调整的两个图像再组合成一个新的亮度图像，两个调整的图像进行结合的表达式为

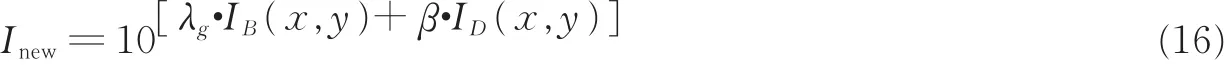
式中：Inew代表增强后的亮度图像；β代表增益系数，它能够控制细节图像的细节波动，对于测试图像，通过代入不同的增益系数发现β设定为14时效果较好。

2.4 颜色恢复

将增强后的图像由HSI色彩空间转换到RGB色彩空间，为防止增强后的图像颜色失真，需要对增强后的图像进行颜色恢复处理，表达式为

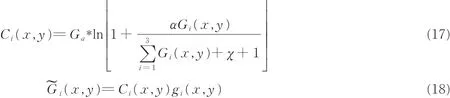
式中：原图像的R，G，B三个色彩分量分别用g1，g2，g3来表示；Ga为增益参数；α调节彩色图像的亮度程度；χ调节图像增强后3种颜色之间的比重；Gi(x,y)(i=1,2,3)分别表示原图像的3个色彩分量；(x,y)为颜色恢复后的3个颜色通道。将这3个颜色通道进行合成可得到本文算法的最终结果。

3 实验与分析

本文实验中选择MSR算法和带彩色恢复的MSR算法(MSR with color restoration,MSRCR)算法在Matlab实验平台(CPU Intel(R)Core(TM)i5-2320 3.0 GHz)上对多幅低照度彩色图像的增强效果进行了对比，验证了本文算法的可实施性和有效性；并且通过主观视觉效果和客观质量评价两个方面对增强图片的效果进行对比和分析。MSR算法，MSRCR算法和本文算法的参数设置如下：（1）MSR算法[12]中 3个高斯尺度参数 σ1=15，σ2=80，σ3=250；（2）MSRCR算法[13]中尺度参数与 MSR算法相同，颜色恢复函数参数，α=6.5，β=0.2，Ga=1.5；（3）本文算法参数如下(引导滤波参数取值)：根据式(9—11)确定窗口半径 r1，r2，r3的取值，平滑参数取值[14]为 ε1=0.000 012，ε2=0.01，ε3=182。3 种算法各采用两种不用的颜色恢复函数参数取值。

3.1 主观视觉评价

图2，3分别给出了两幅代表性的低照度彩色图像分别在3种增强算法下的处理效果。图2中：ηc=20，β=15，α=5.5，χ=0.15，Ga=1.3；图3中：ηc=230，β=15，α=4，χ=0.2，Ga=1.55。

由图2，3对比可以看到：（1）MSR算法虽然可以将黑影覆盖的图像显示出来，但是图像噪声大；图2（b）中下方，远处山峦和近处的树枝没有得到有效的区分；图3（b）中可以看到图像色彩严重失真，右上角图像较暗，已经无法对图像进行正确的处理，出现了类似白色马赛克的图形；同时整体图像处理效果偏灰色，存在光晕伪影现象，图像的层次感不明显，效果较差。（2）MSRCR算法带有颜色恢复处理，图像没有出现颜色失真的情况，但是相较于本文算法还存在一定的差距，如从图2（c）中虽然亮度有所提高，但远处山峦和近处树枝之间的层次仍不明显；图3（c）中白色车辆以及周围环境的明亮处不自然，图像的还原程度不够。（3）利用本文算法的图2(d)中远处山峦和近处的树枝层次比较明显，山峦、凉亭与天空分界清晰；图3（d）中图片亮度明显提高，颜色自然，图像清晰。

由上述实验结果可以看出，本文算法适合处理在天气、光线等较差条件下，亮度和对比度都比较低的彩色图像。

图2 3种增强算法下图片1的效果对比Fig.2 Comparison of three enhancement algorithms for image 1

图3 3种增强算法下图片2的效果对比Fig.3 Comparison of three enhancement algorithms for image 2

3.2 客观质量评价

在图像客观质量评价中，分别针对两组图像给出了原图、MSR算法、MSRCR算法以及本文算法增强后图像的灰度直方图，如图4,5所示，图中横坐标表示图像中各个像素点的灰度级别，纵坐标表示各个灰度级别的像素在图像中出现的频数。

通过对比图4,5可以得到图像的亮度和对比度特征。图4(a)和图5(a)中，灰度直方图大部分出现在偏左位置，说明图像整体偏暗。图4(b)和图5(b)中，灰度直方图只有中间一小段非零值，说明经过MSR算法增强处理后，图像的对比度较低。图4(c)和图5(c)中，灰度直方图大部分依然存在于左边位置，中间有少部分，说明和原图相比，MSRCR算法增强后图像效果不明显。图4(d)和图5(d)中，灰度直方图的非零值几乎遍布整个灰度直方图，说明经过本文算法增强后的图像对比度较高，亮度增强明显。

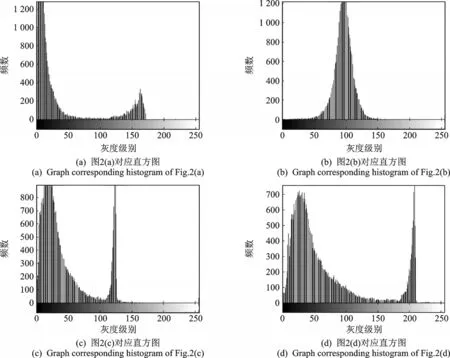
图4 图2(a)—(d)对应的灰度直方图Fig.4 Gray histogram of Figs.2(a)—(d)images

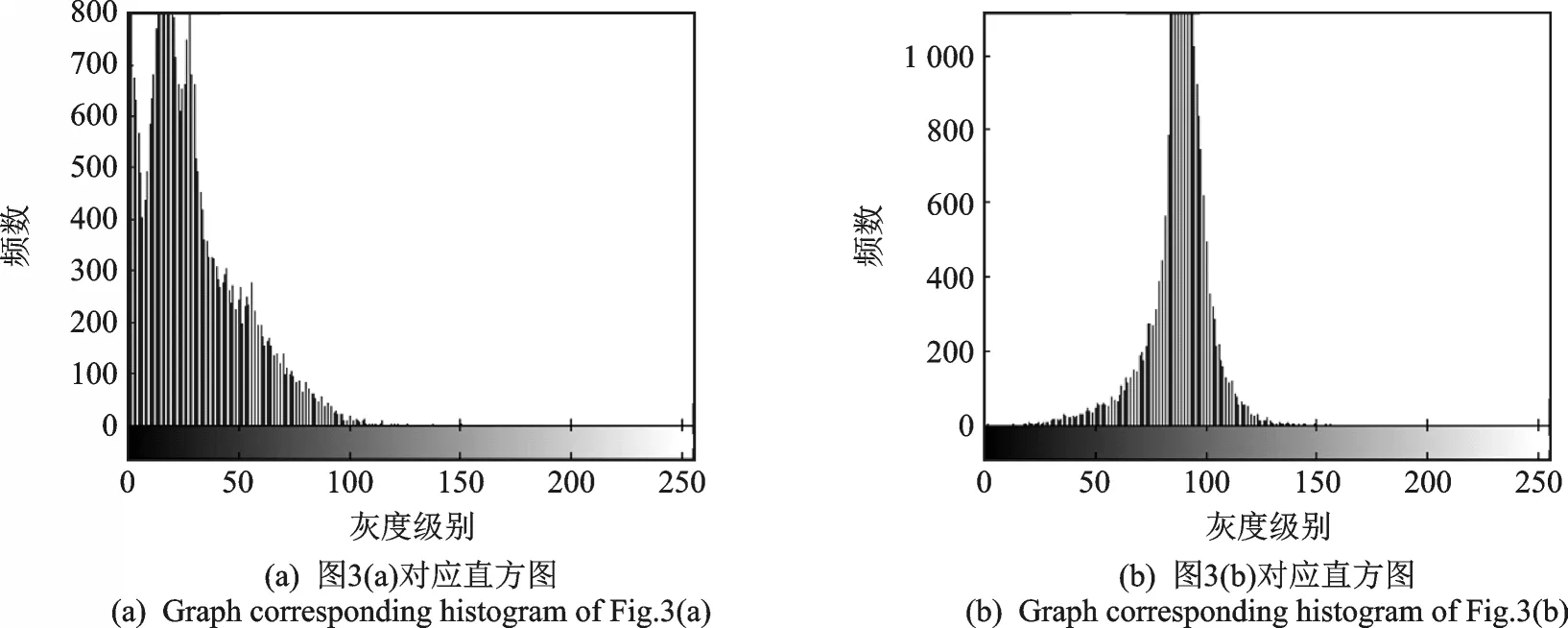
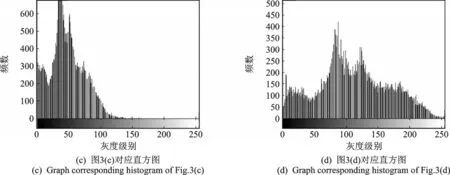
图5 图3(a)—(d)对应的灰度直方图Fig.5 Gray histogram of Figs.3(a)—(d)images

本文采用图像的均值、标准差、灰度熵和彩色熵对图2,3质量进行定量评价[15]：均值表示图像整体亮度的变化，均值的大小表示图像亮度明暗程度；标准差代表图像的对比度；信息熵衡量图像的信息量；彩色熵用于衡量图像的颜色增强程度。结果如表1,2所示。

从表1和表2中可以看出，MSR算法对图像进行增强时，由于出现颜色失真现象，所以均值增加过大，也即平均亮度增强过大，图像对比度较小。而对于MSRCR算法来说，增强后的图像均值较小，即图像的平均亮度增强不明显。本文算法对图像的平均亮度能够进行适当的增强，对比度也有了很大的提高，图像细节表现更明显，颜色增强程度明显提高。

4 结束语

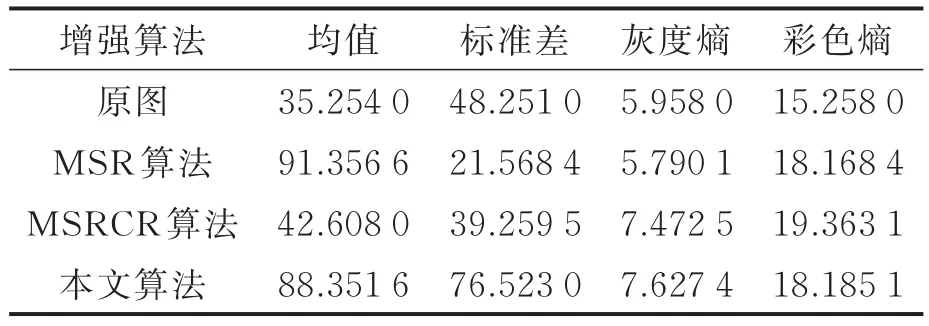
表1 图2定量评价指标Tab.1 Quantitative evaluation index of images in Fig.2

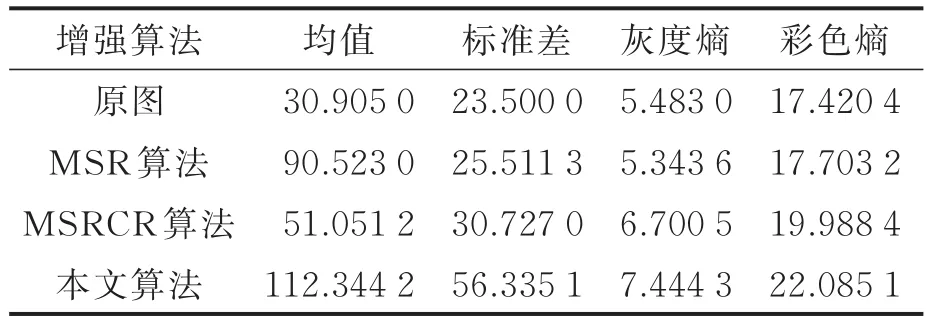
表2 图3定量评价指标Tab.2 Quantitative evaluation index of images in Fig.3

本文在引导滤波的基础上创新性地提出了一种Retinex理论的低照度彩色图像增强算法。该算法将原图像的亮度图像分为两层,分别为细节图像和基本图像。通过使用构造的增益系数对这两层图像进行增强，然后将增强后的两层图像进行重构得到新的亮度图像，最后进行色彩恢复生成新的彩色增强图像。主观视觉效果和客观质量评价结果表明,本文算法可以有效地克服由于光照不均导致的图像色彩失真现象，图像亮度和整体识别度显著提高，尤其对图像亮度较低的区域有较好的增强效果，图像细节丰富、对比度强，提高了对无人机获取的低照度图像的分析效果。