多尺度并行坐标插值实时图像克隆算法

沈晔湖 蒋全胜 汪帮富 朱其新

（苏州科技大学机械工程学院，苏州，215009）

引 言

作为一种图像编辑技术，图像克隆能够将源图像中的克隆区域嵌入目标图像的指定位置，并且实现该区域与目标图像背景的自然融合，使用户在观察目标图像时不会产生明显的突兀感。

对人类视觉系统的研究表明：人类视觉系统对场景局部亮度差异的敏感度要远高于亮度的绝对值本身[1]。基于该理论，传统的图像克隆技术在保持克隆区域内部颜色梯度分布的前提下保证克隆区域的边缘与目标图像对应位置颜色的相似性，这一般通过求解泊松方程来实现。Perez等[2]证明求解泊松方程等价于求解包含狄利克雷边界条件的拉普拉斯方程，该边界条件设置为克隆区域边界在源图像和目标图像处的色彩差异。上述问题最终可通过求解大规模稀疏线性系统来得到。Adobe公司从Photo⁃shop 7开始支持类似于图像克隆效果的修复笔刷工具。该笔刷工具通过求解四阶偏微分方程的手段保证克隆区域内部梯度值的连续性[3]。Agarwala等[4]提出将多张图像中的内容融合的算法，采用Graph-cut优化技术选择不同图像中的最优融合边界，图像融合仍通过求解泊松方程来实现。Jia等[5]发现泊松图像编辑的效果依赖于克隆图像区域的边界，因此提出了采用最短闭合路径算法来提取最优的克隆区域边界。

求解泊松方程的运算复杂度和内存消耗均较高。为了克服上述缺陷，Agarwala[6]利用自适应四叉树细分技术构建了约简的线性系统进行求解，该方法仅可以用于加速特定问题如图像拼接领域泊松方程的求解。McCann和Pollard[7]提出了基于GPU的多重网格泊松求解器，可以实现快速的图像克隆，然而该算法的具体实现难度较大且运行时对显存的需求较高，作者在文中指出当算法对内存的需求超过显存容量时，算法性能会大幅度下降。

除了上述复杂的求解泊松方程的方案，Farbman等[8]发现泊松图像克隆的本质是构建一个调和插值从而将区域边界的不一致性扩散到区域内部。他们利用均值坐标技术直接通过图像插值产生平滑的内部区域，从而避免了求解泊松方程。由于该方法利用了图像插值技术，所以算法实现非常容易。但是该方法插值系数的构造计算量较大，导致其运算复杂度很高。为此，作者提出了通过自适应网格等预处理方法，从而在一定程度上降低了图像插值阶段的运算复杂度。但预处理手段的引入导致图像克隆整体过程无法实现实时运算，而且预处理步骤较复杂，使得该算法实现的难度大幅上升。

近年来，图像克隆研究主要集中在改善图像克隆视觉效果方面。如Tanaka等[9]通过一种改进的泊松方程实现了在克隆和背景区域颜色差异较大情况下的平缓过渡；李贝等[10]在均值坐标技术基础上提出了利用局部亲和力传播算法改善图像克隆中的颜色不协调问题；黄美玉等[11]通过构建光照一致的数据约束和马尔科夫随机场函数进行求解的方式解决了源图像和目标图像光照环境不一致的问题；文献[12]通过引入颜色不变量模型得到图像光照判断参数，进而对克隆选区进行自适应的颜色匹配。上述算法运算复杂度均较高，处理100万像素的图像克隆区域的时间均在秒级。

鉴于目前较少有针对图像克隆算法的简易实时化研究，本文基于文献[8]，提出了一种改进的均值坐标权重系数的计算策略，大幅降低权重系数的计算复杂度，避免了实现较复杂的预处理步骤。此外结合多尺度图像处理技术以及并行加速技术进一步实现加速，从而在当前主流GPU上实现了对100万像素图像区域的实时克隆。定性和定量实验结果均表明本文提出的方法得到的结果与文献[8]十分接近。

1 均值坐标图像克隆

1.1 均值坐标简介

为保证本文的可读性，首先简要介绍2D均值坐标的基本概念，详细内容参见文献[13]。

如图1所示，对于2D图像内的一个区域P，定义该区域的边缘为∂P，包含m个像素：p0,p1,…,pm-1,pi∈R2。为不失一般性，定义：pm=p0。从而区域P内的像素x相对于∂P的均值坐标可定义为

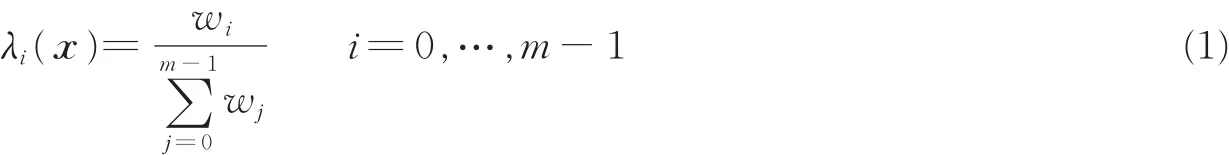
图1 图像均值坐标的定义Fig.1 Definition of mean-value coordinates

式中

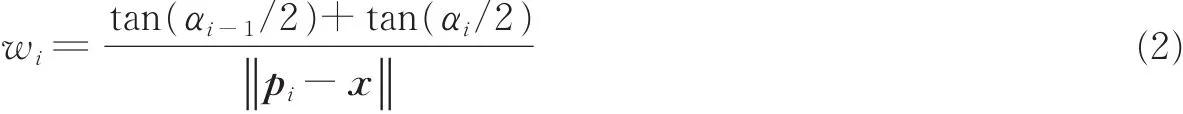
式中||·||表示L2范数。

1.2 均值坐标图像克隆算法流程

实现图像克隆算法的基本流程如下[8]

步骤1 计算均值坐标。对于区域P内的每一个像素x，根据式（1，2）计算其相对于∂P的均值坐标并保存。

步骤2 计算区域边缘处的前背景色彩差。对于∂P中的每一个像素pi，通过式(3)计算前背景色彩差并保存。

式中：It(pi)和Is(pi)分别为pi处目标图像和源图像的RGB值组成的矢量。

步骤3 对于每一个区域P内的像素x，计算其均值坐标插值结果。首先利用下式计算颜色校正矢量

像素x的最终颜色值的计算方法为

2 本文方法

图2给出了本文算法的总体流程图。对于1.2节的算法，其运算复杂度最高的部分是步骤1。假设区域P内的像素个数为n，其边缘∂P包含m个像素，通常n≫m。步骤1中调用式（2）计算次数的数量级为O(nm)。但是式（2）中需要计算两个角的正切值，而且两个角度本身还需通过余弦定理计算得到，因此复杂度较高，造成算法无法实现实时处理。为此，文献[8]提出利用预处理算法减少n和m，从而降低式（1）的运算复杂度以及调用式（2）的次数。但是为了减少n和m引入的预处理算法本身复杂度不低，文献[8]中报告对于100万像素的克隆区域的预处理时间在1 s以上，因此导致图像克隆算法整体无法实现实时处理。

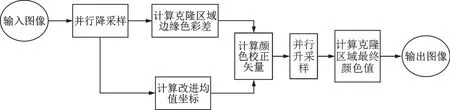
图2 算法总体流程图Fig.2 Flowchart of the proposed algorithm

2.1 改进的均值坐标

与文献[8]不同，本文提出的算法通过合理的近似技术直接简化式（2）的计算，以降低整体的运算复杂度。

根据麦克劳林公式，当x接近0时对tan(x)进行级数展开并取一阶近似可得到

将式（6）代入式（2）可得

为不失一般性，假设∂P是由4-连通的像素组成，因此对于∂P上的任意两个相邻像素pi和pi-1，它们之间的距离恒为1。可以验证当区域P内的像素x与像素pi和pi-1之间距离在5个像素以上时，角度αi接近0，上述近似的误差约为0.33%。因此对于区域P内的绝大多数像素x，式（7）是对式（2）的较优近似。

式（7）仍需要计算两个角度 αi-1和 αi，为了进一步简化式（7）的计算，本文提出了如下算法。如图3所示，顶点 pi-1,pi和 x组成三角形，αi-1=∠pixpi-1，虚线xq为αi-1的角平分线，它与边pi-1pi的交点为p‘。圆弧piq是以x为圆心，||pi-x||为半径的圆弧段。根据圆弧的定义，有

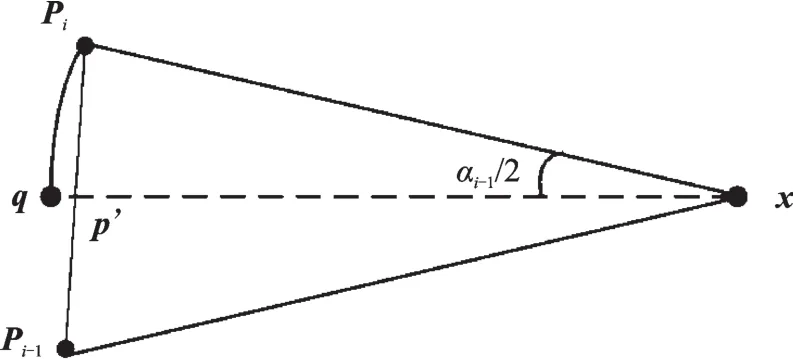
图3 均值坐标的简化计算Fig.3 Simplified calculations of mean-value coor⁃dinates

式中：||piq||a为圆弧piq的长度。如前所述，||pi-pi-1||=1并且αi-1/2接近于0，因此可以将||piq||a近似为||pi-pi-1||的一半也即0.5，从而式（8）可以近似为（请参考附录A关于该近似的可行性验证）

类似地可以得到

将式（9，10）代入式（7）可得

比较式（11）和式（2）可知式（11）只需计算pi和x的距离平方，无需计算任何角度，因此比式（2）节约了2次角度计算、2次正切计算和1次开方计算，从而实现了大幅度的简化。

由于最终的克隆区域颜色校正结果可根据式（4）均值坐标相对权重的线性组合来得到，而通常情况下边缘∂P包含的像素个数m在103数量级，因此通过式（11）计算得到的少量权重误差通过上述线性组合的平均效应后不会对最终的校正结果产生大的影响。这将在实验结果部分作详细验证。

2.2 多尺度并行加速

根据式（5），克隆区域内像素的最终颜色值取决于颜色校正矢量r(x)。r(x)是克隆区域边缘像素处颜色差的线性组合。根据式（1，4，11），在克隆区域内部r(x)是平缓变化的，受文献[14]的启发，本文提出采用多尺度并行的手段进一步加速计算。首先将源图像和目标图像降采样[15]；其次对降采样的克隆区域用并行加速手段计算每个像素的颜色校正矢量r(x)；然后将克隆区域对应的颜色校正矢量r(x)进行升采样[15]，使得分辨率达到初始状态；最后利用r(x)计算克隆区域内像素x的最终颜色值。其具体步骤如下：

步骤1 利用并行双线性插值算法[16]对It和Is进行降采样，降采样的尺度为s，本文中s=1/2，得到降采样后的图像。

步骤2 利用并行加速手段计算降采样图像对应的颜色校正矢量rd(x)。该步骤又可分为如下两步：

(1)根据式（3）计算克隆区域边缘处前背景色彩差并保存；

(2)通过GPU并行加速技术[17]计算降采样的克隆区域Pd内部每个像素x对应的颜色校正矢量rd(x)，具体算法如本节后面描述。

步骤3 利用并行双线性插值算法[16]对rd(x)进行升采样，升采样的尺度为1/s，得到初始分辨率下的颜色校正矢量r(x)。

步骤4 计算克隆区域内每个像素x的最终颜色值。

对于步骤2的第2步，可将每个线程设置为利用式（5）计算每个像素x对应的颜色校正矢量rd(x)，算法步骤如下：

输入：区域的边缘像素集合∂Pd，区域内部像素集合Pdin，区域边缘前背景色彩差集合diffd。

输出：颜色校正矢量rd(x)。

（1）计算线程ID号i；

（2）提取第i个区域内部像素x=Pdin(i)；

（3）对于∂Pd中的每个像素pj，利用式（11）计算wj并保存；

（4）根据式（1）计算x对应的均值坐标并保存；

（5）根据式（4）计算颜色校正矢量rd(x)。

综合上述算法描述，其伪代码如下。

输入：源图像Is、目标图像It、克隆区域内部像素掩模图像Pin

输出：克隆图像Ic

Isd=downsample(Is,s) #利用文献[16]算法对Is进行并行降采样，降采样的尺度为s

Itd=downsample(It,s) #利用文献[16]算法对It进行并行降采样，降采样的尺度为s

Pind=downsample(Pin,s) #利用文献[16]算法对Pin进行并行降采样，降采样的尺度为s

for i=1 to md

diffi=Itd(pi)-Itd(pi) #根据式（3）计算降采样后克隆区域边缘处前背景色彩差并保存

end for

parallel for i=1 to nd#对每个像素并行处理

x=Pdin(i) #提取第i个克隆区域内部像素

sum_w=0

for j=1 to md

sum_w=sum_w+wj

end for

rd(x)=0 #初始化为零向量

for j=1 to md

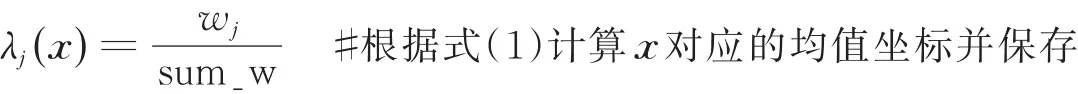
rd(x)=rd(x)+λj(x)⋅diffj#根据式（4）计算颜色校正矢量rd(x)

end for

end parallel for

r=upsample(rd,1/s) #利用文献[16]算法对rd进行并行升采样，升采样的尺度为1/s。

parallel for i=1 to n #对每个像素并行处理。

x=Pin(i) #提取第i个克隆区域内部像素。

Ic(x)=Is(x)+r(x) #利用式（5）计算克隆图像Ic内部像素的颜色值。

end parallel for

3 实验结果

3.1 定性分析

本文构建了一个包含20组测试图像的数据集，每组测试图像包含源图像、目标图像、手工标记的源图像中需要克隆的区域和手工标记的目标图像克隆放置区域。

图4 第1组测试图像实验结果Fig.4 Results of test example 1

图5 第2组测试图像实验结果Fig.5 Results of test example 2

图6 第3组测试图像实验结果Fig.6 Results of test example 3

图4 —7展示了4组测试图像的例子，比较图4—6中的（d），（e）以及（f）可知本文提出的算法和文献[12]以及文献[8]中的算法结果差别细微，肉眼几乎难以察觉。这也从定性角度验证了本文改进均值坐标方法的可行性。

图7展示了“变脸”特效，美国总统特朗普和俄罗斯总统普京的脸部区域互换后的效果自然，验证了本文算法可以实现逼真的视觉特效。

图7 “变脸”特效Fig.7 “Face/off“effect

3.2 客观评价

本节以文献[8]合成的克隆区域图像为基准，将本文提出算法合成的克隆区域图像与其进行比较，计算颜色误差。图8分别显示了第1组和第3组测试图像中的克隆区域颜色误差分布图像。在计算下述图像中每个像素的误差值时采用如下方式：用本文提出算法和文献[8]合成算法计算每个像素处的颜色误差，该颜色误差的取值为R,G,B三个分量中误差绝对值的最大值（每个像素三通道亮度级范围是0～255）。本文还统计了20组测试图像中克隆区域的平均颜色误差值分布统计直方图，结果如图9所示。

从图8,9可以看到，克隆区域内大部分像素和文献[8]算法的颜色误差在2个亮度级以内，误差在4个亮度级以上的像素占比在0.9%以内。同时还计算了本文算法合成结果相对于文献[8]合成算法在克隆区域内的峰值信噪比(Peak signal to noise ratio,PSNR)值[18]，结果如表1所示。从表1中的统计结果可知，本文方法克隆结果和文献[8]克隆结果极为相似，这也从定量角度印证了3.1节中的定性分析结果。

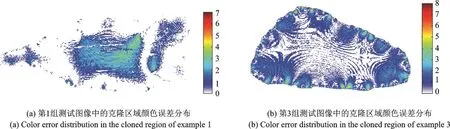
图8 克隆区域内部的颜色误差分布图像Fig.8 Color error distribution images in the cloned region

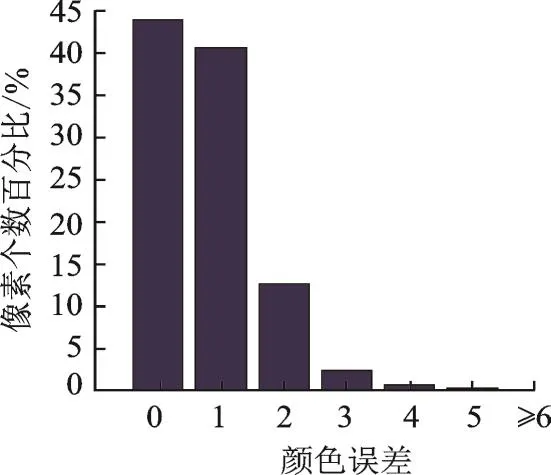
图9 克隆区域内部平均颜色误差值分布统计直方图Fig.9 Color error distribution histogram in the cloned region

表1 20幅测试图像中克隆区域的PSNR值Tab.1 PSNR in cloned regions of twenty test images d B

3.3 主观评价

为了对比文献[8]中算法与本文算法的主观视觉效果，选取了20名被试者对20组测试图像分别用两种算法得到的结果进行评分，评分范围是1～10分。20名被试者男女各半，年龄范围是19～40周岁，涵盖了本科生、研究生以及学校教师，并且都与本文项目无关。

实验中每次在计算机屏幕上左右分别显示一组测试图在文献[8]中算法与本文算法的结果。为了消除被试者打分的倾向性，在每组测试结果显示过程中随机设定两种算法结果的左右显示位置。被试者分别对左图和右图的主观结果进行打分。

实验结果表明14人对20幅测试图像中两种算法的结果打分完全相同，也就是说有14人主观评价认为两种方法克隆图像的效果完全一致，另外6人的结果如表2所示。

由表2可知，6人中对两种算法结果的评价分最大只相差1分，且两种方法在20幅测试图像中的平均得分非常接近，这也从一个侧面表明文献[8]中算法与本文算法的结果非常类似。

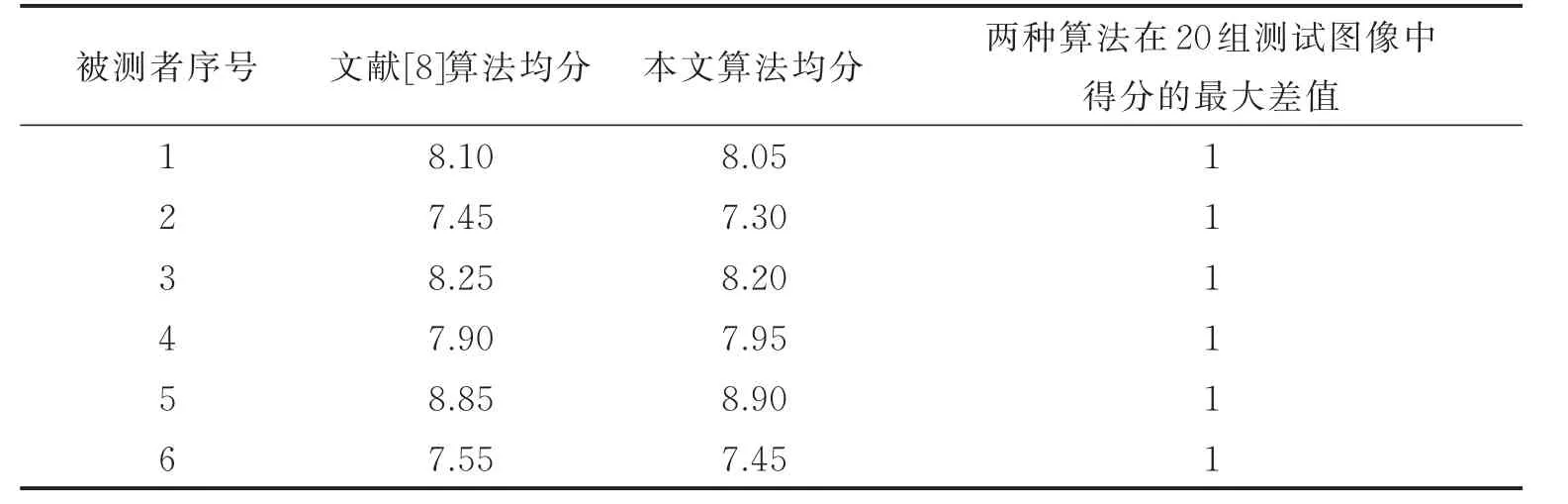
表2 20幅测试图像中两种算法主观评分结果比较Tab.2 Comparisons of subjective scorins of two algorithms for twenty test images

3.4 降采样尺度s的设定

在2.2节中，本文算法需要确定一个超参数降采样尺度s，为此本节实验选择了不同的 s值，分别为 1，1/2，1/4，1/8和1/16，对每组测试图像分别获得5张不同的克隆图像结果。与3.2节类似，计算并比较了20组测试图像在不同s值下的平均PSNR均值，结果如图10所示。

由图10可知当s取1/2时，PSNR均值仍在45 d B以上，这与不进行降采样（即s=1）的结果接近。但当s取1/4及以上时，PSNR均值有大幅衰减，已经影响到主观的评价结果。综合考虑图像克隆效果与运算复杂度，本文中所有实验均取s=1/2。

3.5 执行时间分析

实验平台配置为Intel 3.4 GHz i7-4770 CPU，显卡为NVidia Geforce GTX 960，内存为8 GB。本节中比较了文献[12]、文献[8]方法和本文提出算法的执行时间。由于文献[8,12]并未开源其代码，因此本文实现了其算法。所有算法均用C++实现，其中GPU并行加速部分代码利用CUDA实现。

图11展示了平均的单次式（2）执行时间和本文简化后的单次式（11）在CPU上执行时间的对比。由图11可见，本文简化后的式（11）执行时间约为3.5 ns，从而达到了约30倍的速度提升，证明了本文算法对于简化均值坐标权重计算的有效性。

表3展示了不同图像克隆区域尺寸下本文算法运行时间和文献[8]以及文献[12]算法之间的比较。表中第3列和第4列分别为文献[12]和文献[8]算法实现图像克隆完整流程所需的时间，其中括号内的数字为整个流程中预处理算法的耗时，本文算法提出的算法无需任何预处理步骤。由表3可见本文方法实现了对100万像素的图像区域的实时克隆，即使当克隆区域增大至400万像素的高分辨率时仍能达到5帧/s左右的速度。

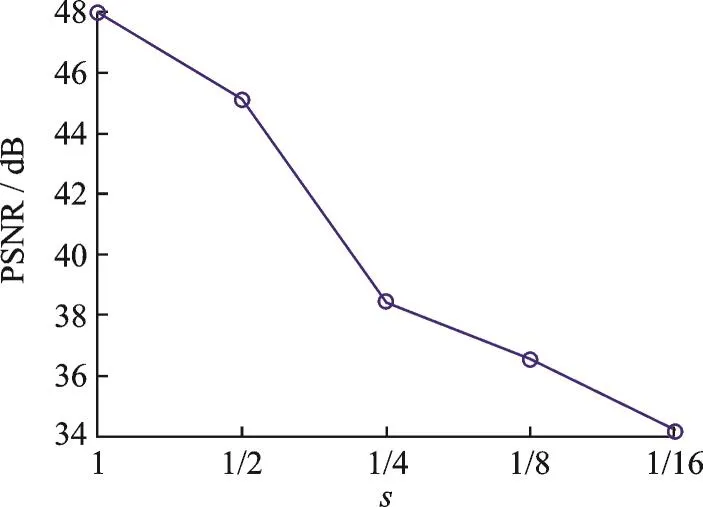
图10 不同s值时的PSNR均值比较Fig.10 Comparison of average PSNR un⁃der different values of s

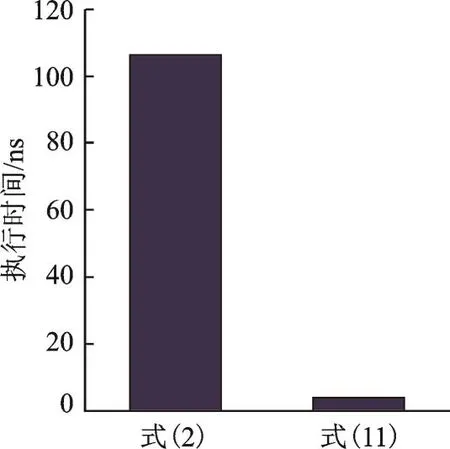
图11 式（2）和式（11）计算执行时间对比Fig.11 Comparisons of execution time for Eq.（2）and Eq.（11）

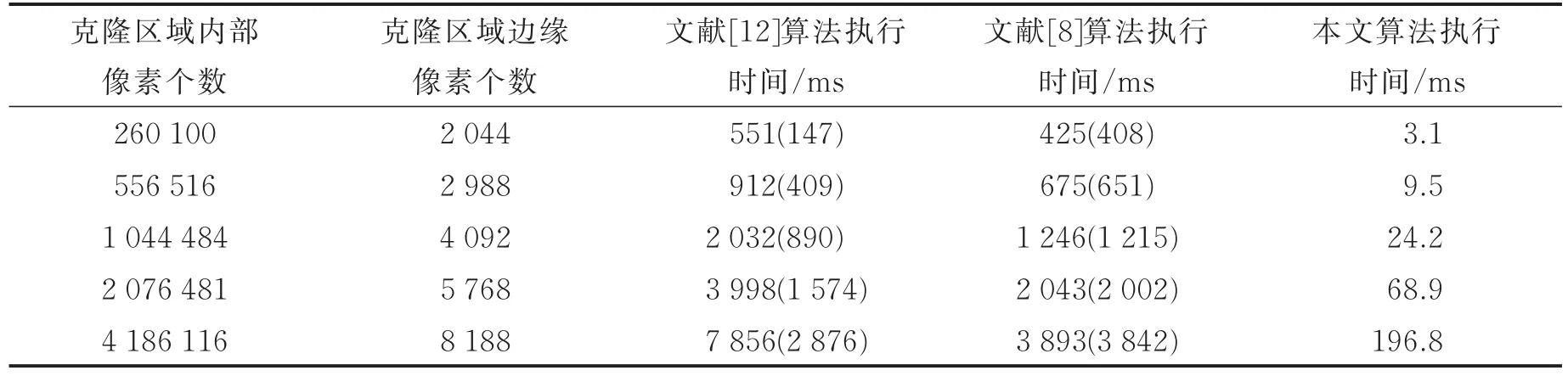
表3 不同算法的运算执行时间结果比较Tab.3 Compar ison of execution time for differ ent algorithms

4 结束语

本文分析了传统基于均值坐标的图像克隆算法的运算瓶颈，通过提出一种简化的均值坐标计算方案在无需任何预处理步骤的前提下大幅降低了均值坐标的运算复杂度，并进一步利用多尺度GPU并行加速方案实现了对100万像素图像区域的实时克隆。客观和主观实验结果表明本文算法在克隆结果与文献[8]中方法结果差别细微的前提下可以大幅提升高分辨率图像的克隆效率。

附录A 式（8）近似可行性的验证

由于pi和pi-1为两个相邻像素，不失一般性，假设在图3中三角形两边长相等,即||pi-x||=||pi-1-x||=a。又由于||pi-pi-1||=1，根据余弦定理可得

因此，对式（8）用式（9）进行近似的相对误差为

图A 1显示了相对误差值e和三角形边长a之间的关系。

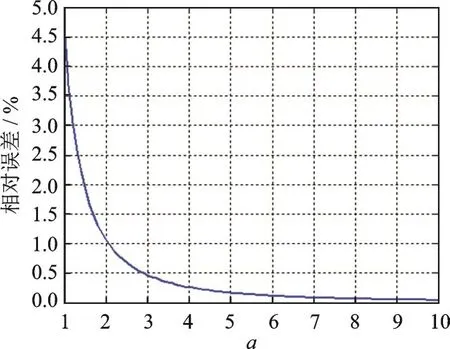
图A 1 相对误差值e和三角形边长a之间的关系
Fig.A 1 Relation between relative errors e with the triangle edge length a

由图A 1可知，当区域P内的像素x与像素pi和pi-1之间距离在3个像素以上时，上述近似的误差已经低于0.5%,由此验证了式（9）近似式（8）的可行性。