一种基于有界变分的树叶锯齿特征提取算法研究
2019-02-27李德志成孝刚吕泓君李海波
李德志 成孝刚 汪 涛 吕泓君 李海波
(南京邮电大学通信与信息工程学院,南京,210003)
引 言
植物的叶片形态各异,有扇形、椭圆形、掌形、披针形等,提取树叶表面形态特征,尤其是锯齿特征,有助于构建树叶表面特征与其基因之间的关系,对于植物育种、抗病虫具有重大意义。
目前已有诸多方法提取植物叶片边缘轮廓和锯齿的特征。国外对于植物叶片提取特征的研究起步较早,提取的参量也相对全面[1]。Belongie等人[2]在2007年提出了形状上下文描述方法,利用直方图对目标图像的形状特征进行描述,很好地反映了轮廓线上采样点的分布。Mouine等人[3]在2013年提出三角形面积法、三角形边长表示法、三角形角度法以及三角形边长角度法进行曲率尺度空间的描述。Wang等人[4]采用拱形高度即轮廓线上一点到其对应的弦的垂直距离来作为特征描述。国内,王晓洁等人[5]设计了基于凸包的植物叶锯齿与叶裂位置识别方法,并且对多种植物叶图像进行了测试。董本志等人[6]采用基于Freeman的拐角点检测方法排除大部分伪拐点,并结合基于链码差的边界凹凸性判别方法进一步排除伪拐点,同时标注出叶片的顶点。尽管上述方法对植物叶片锯齿边缘特征的识别有了改善,但是仍然存在识别锯齿个数准确度较低、提取的特征参数不够多、对大数据量叶片泛化能力差、无法批量提取锯齿特征等局限性。
针对上述问题,本文采用了基于有界变分的方法检测叶片的锯齿数量等各种参量,引入有界变分思想,对锯齿深度进行分析,算法流程如图1所示。利用海量数据进行算法训练,验证了算法的有效性。
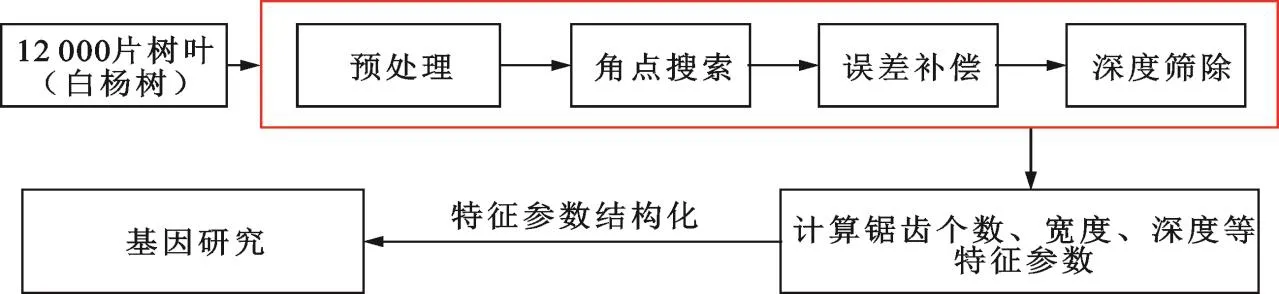
图1 树叶锯齿特征提取研究流程Fig.1 Research process of feature extraction of leaf serration
1 基于有界变分的算法
1.1 理论基础
本文算法所处理的数据为树叶扫描图像,拟采用有界变分构建树叶锯齿特征提取方法。Rudin等人先后构建并完善了关于图像处理的变分模型[7-9],该模型首先假设噪声为高斯白噪声,且均值方差为零。具体图像的变分模型可表述成[10]

式中|Ω|表示图像区域Ω的面积。按照有限差商来解释ux,则有

可以看出,BV(u)具有如下性质:若 u ∈ BV([x1,x2]),且在[x1,x2]内单调,u(x1)=u1,u(x2)=u2,则无论函数u的具体形式如何,只要u在边界点x1,x2内可导,总有[10]

1.2 基于有界变分的锯齿特征提取算法
式(3)的本质是求变差。在此基础上,本文所提出的树叶锯齿特征提取算法包含图像预处理(轮廓坐标提取)、搜索锯齿顶点、搜索锯齿凹点、计算锯齿个数、宽度以及深度等环节,具体阐述如下。
1.2.1 轮廓坐标提取
本文在提取锯齿特征之前先对树叶图像进行基本的预处理,获得树叶边缘轮廓坐标。轮廓坐标提取的准确与否,会直接影响到锯齿特征提取的好坏,因此这一步至关重要。首先对彩色图片进行灰度化处理,消除灰度高频噪声;然后将灰度图像二值化,并填充图像中的空洞等不完全部分,获取单个连通体,指定起始点坐标与跟踪方向,较为准确地提取叶片的轮廓坐标;最后,沿着顺时针方向将轮廓坐标分为4个部分,分别存入4个矩阵,供后续分段处理。设N为边缘坐标矩阵,b_top,b_right,b_bottom,b_left分别为边缘上顶点、右顶点、下顶点、左顶点的坐标,(i,j)为边缘像素坐标,则 N1[i,j]={(i,j)|i≥ b_top[1,1]&j< b_right[1,2]},类似依次将坐标分别保存入 N1,N2,N3,N4中。图2(a)显示了图像原始轮廓,而图2(b)显示了图像轮廓的4个部分。
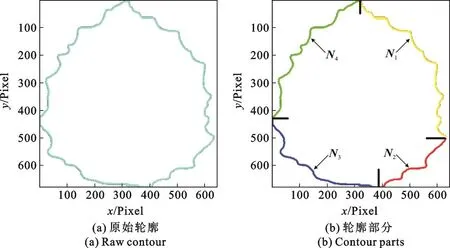
图2 树叶轮廓提取Fig.2 Leaf contour extraction
1.2.2 基于变分的锯齿顶点提取
本文中以轮廓第1区域为例(N1),通过多重筛选搜索角点,具体包含斜率搜索、误差补偿和深度筛选3个步骤。
(1)斜率搜索
基于凸包生成算法[11],本文以斜率代替角度计算,作为角点搜索的第一步。
①根据式(4)计算出目标轮廓上从b_top到b_right之间各点到b_top点的斜率为

②选出上述计算出的斜率中最小值的索引,确定位置为
③以上面计算出的首个位置作为起点,重复①②操作,直到到达b_right,到此为止进行了第一轮搜索,将位置索引保存到I1。
由于锯齿的多样性,通过斜率变化搜索出的顶点并不能覆盖所有实际的顶点,有一定的缺失
(2)误差补偿
观察叶片图像锯齿,可以看到一般锯齿深度都存在大小变化。基于式(3),本文假定锯齿的深度信号在局部邻域内单调变化,利用求解锯齿深度变差,对第(1)步斜率搜索进行误差补偿。具体操作中,计算点到由锯齿顶点构成直线的距离变化来进行第二轮补偿选择。假设I1中第一个索引为a1,第二个索引为a2,从a1到a2之间的区域为N11,以N11为例描述详细过程。
①根据式(6,7)计算出由a1,a2构成的直线方程。

②根据式(8)计算出N11中所有坐标点到由a1,a2构成的直线的距离,从中筛选距离从大到小,再从小到大的点,作为新的顶点。
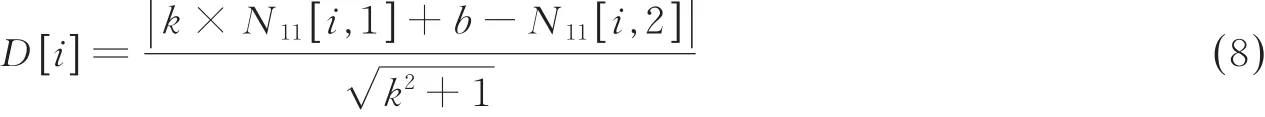
③对N1中的其他区域重复步骤①,直到N1区域中的顶点扫描完毕,到此为止进行了第二轮搜索,将新筛选出的顶点位置索引联合I1中的位置索引一起保存到I2中。
虽然通过斜率搜索和误差补偿可以搜索出大量的顶点,但是由于轮廓上锯齿凹凸程度不同,其中很多顶点位于实际顶点的内部,并不需要,有一定的冗余。
(3)深度筛除
叶片图像中有很多轻微凹凸的曲面,并不能在实际意义上被称为锯齿,但是由于上述两个方法的涵盖性强,达到了一定的“过拟合”。故这里采用了与式(8)类似计算距离的方法,计算出I2中所有索引坐标到I1中顶点索引坐标所构成直线的距离,选取阈值,筛除不符合的顶点,最终将符合的顶点保存到I3中,如式(9)所示。
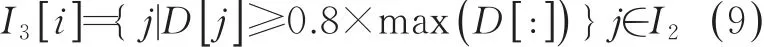
1.2.3 提取锯齿凹点
I3中所有顶点即本文最终提取出的锯齿顶点。将其中所有两两顶点连线,求出方程。通过距离公式求出锯齿顶点之间所有的坐标点到方程的距离,取其中最大距离的坐标点作为当前锯齿的凹点,如式(10)所示。
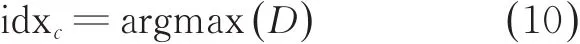
1.2.4 计算特征参数
上述算法提取锯齿凹点时,计算出的对应最大距离即为当前锯齿的深度,I3中相邻锯齿顶点之间的距离即为锯齿的宽度,而且提取出的锯齿凹点个数就是锯齿的个数。论文算法的详细步骤如表1所示。

表1 本文算法详细步骤Tab.1 Detailed process of proposed algorithm
2 计算机验证及分析
本文利用瑞典的白杨树叶对所提算法进行验证,共计1 200棵白杨树,每棵树采集10片树叶,共计12 000张。验证算法的计算机硬件为:CPU Intel(R)Core(TM)i5-6300HQ,内存8 GB,所有软件平台为Python和Matlab。
图3为部分树叶测试结果。左列图像为在每个二值化图像轮廓上用外部线条连接识别的锯齿顶点,然后通过内部线条两两连接顶点与凹点,形成三角,最后用数字标注出锯齿的个数。右列则对应左边叶片图像的锯齿参数计算结果,包括锯齿深度及锯齿宽度。
由图3可以看出,4张叶片图像均经过初步角点搜索、误差补偿及深度筛除等多轮步骤确定锯齿位置,较为准确地标注出锯齿顶点及凹点。
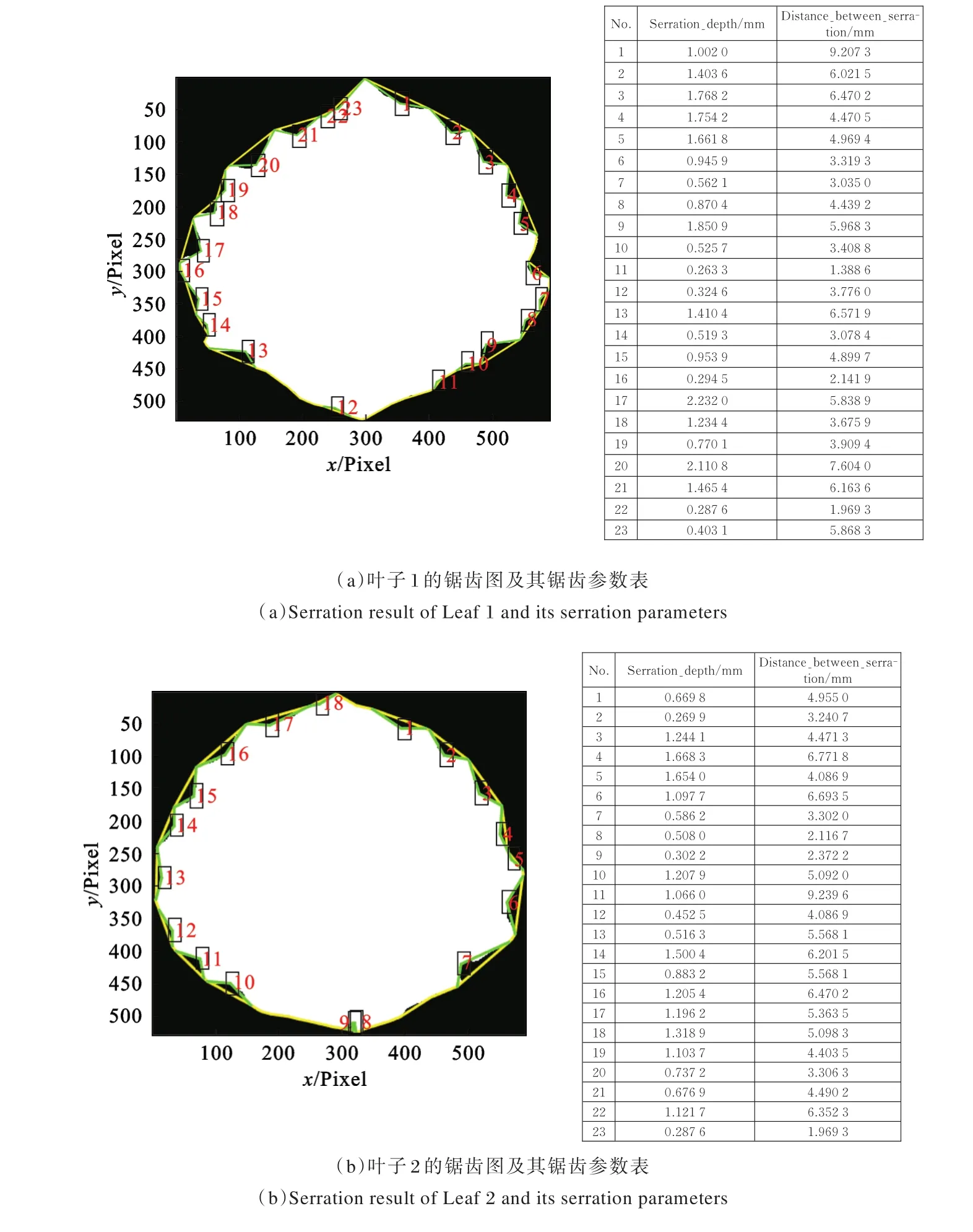
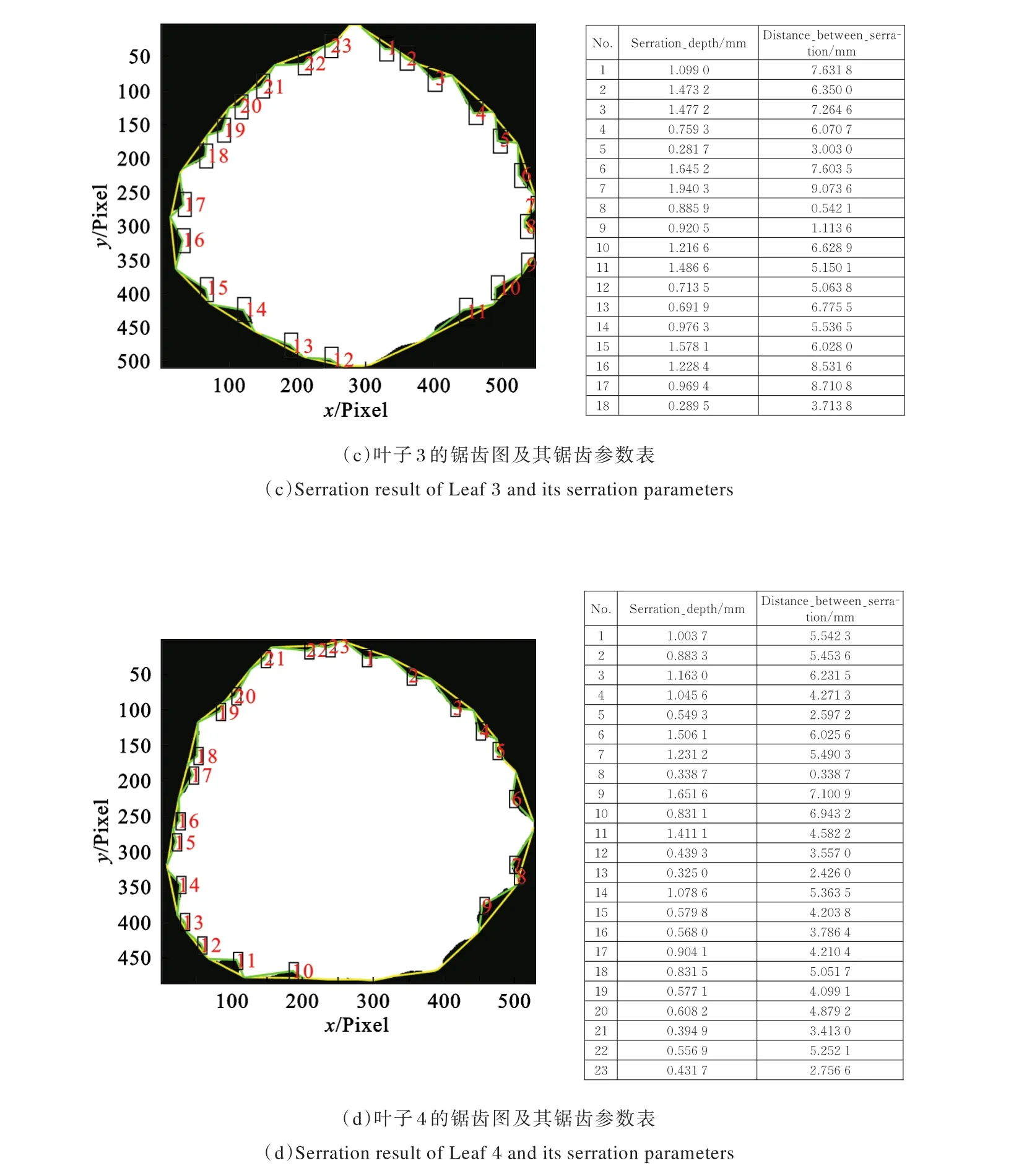
图3 数据验证结果Fig.3 Data verification result
图4 显示了300张叶片样本的锯齿个数检测结果,横轴表示叶片的个数,纵轴表示对应的检测个数。蓝色线表示了算法预测的个数,黄色线表示了实际观测的个数。据测试结果计算,识别锯齿个数的准确率达86.3%。在此基础上,能够准确计算出锯齿宽度、深度等参数。需要说明的是,树叶底部较为平滑时,一般不被视为锯齿。
3 结束语
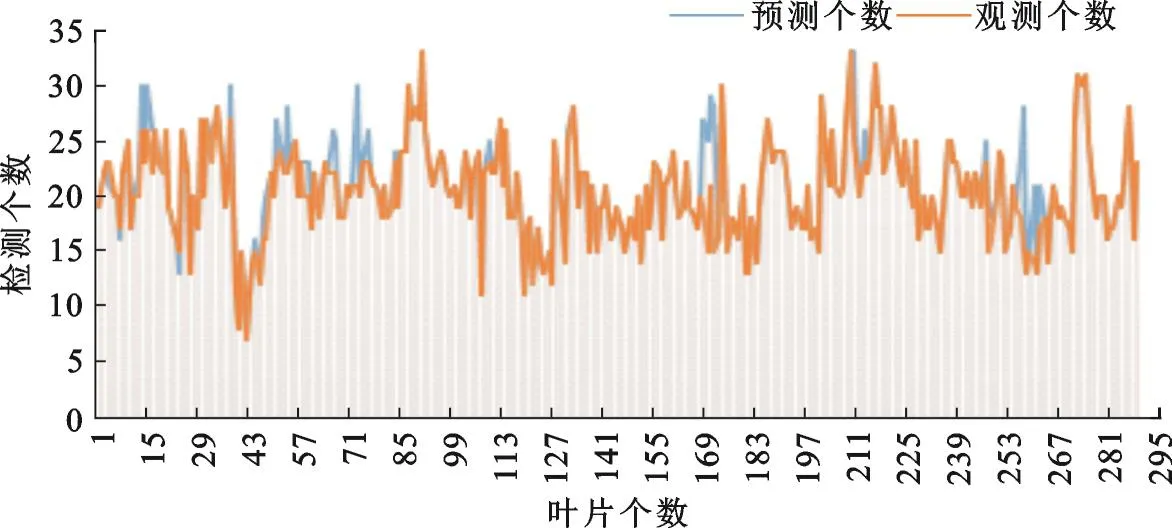
图4 锯齿个数检测结果Fig.4 Detection result of serration numbers
本文提出了一种基于有界变分的树叶锯齿特征提取算法,在提取树叶轮廓坐标的基础上,计算叶片相邻像素点之间的斜率变分,搜索锯齿顶点及凹点,最后计算树叶锯齿的数量、深度和宽度等多维特征。经过测试,识别锯齿个数的准确率达86.3%,同时能够在此基础上计算出锯齿深度、宽度等参数,为后续的基因分析提供依据,具有一定的参考价值。
但是,本文算法还存在一定的局限性,检测还存在一定误差。究其原因,一方面是预处理不够完善,仍有噪声点出现,不能特别准确地提取轮廓坐标;另一方面可能是多轮筛选提取的过程中,筛选的顺序或次数有问题。后续将针对这些问题进行改进。同时,深度学习数据特征提取方面显现出良好的性能。利用深度学习对树叶特征作分析,并与本文算法比较,将为本文后续工作。
