基于应变模态的模态应变能损伤识别方法*

周计祥， 吴邵庆,2， 董萼良,2， 费庆国,2

(1.东南大学工程力学系 南京，210096) (2.东南大学江苏省工程力学分析重点实验室 南京，210096)

引 言

工程结构的安全问题至关重要，使得结构健康监测[1]成为热门的研究领域之一。结构在服役过程中容易产生损伤，影响结构安全，结构健康监测中的损伤识别一般可分为4个层次：a. 结构是否发生损伤; b. 确定损伤的位置; c. 确定损伤程度; d.评估结构剩余寿命。结构中出现损伤会引起其动力学参数发生变化，如结构模态参数等。通过对比损伤前后结构的固有频率、振型[2]等模态参数的变化，可以判断结构是否发生损伤，然而由于固有频率和振型等为全局参数，局部损伤对其敏感性较低，准确地定位损伤甚至定量损伤，仍存在一定的难度。基于模态应变能的损伤识别方法[3]是基于模态振型构造的单元模态应变能的识别算法，具有良好的损伤敏感性和噪声鲁棒性。

目前，基于模态应变能识别的结构损伤研究已有一定成果。Shi等[4]提出基于位移模态的模态应变能损伤识别方法，利用数值仿真验证了该方法对复杂结构损伤定位的有效性。Law等[5]针对转角自由度难以准确测量的问题，采用对实测位移振型信息扩充的方法获取转角自由度信息。结果表明，基于振型扩充的模态应变能损伤识别算法可以有效提高结构损伤定位的精度。Hu等[6]提出了基于位移模态的交叉模态应变能法，该方法可以有效定位损伤和评估损伤程度。

以上研究均基于位移模态开展，由于应变振型比位移振型具有更丰富的信息，基于应变模态的结构损伤识别方法也有一定的研究成果。Xu等[7]提出了一种基于应变模态的损伤识别算法，通过建立损伤指标与应变振型变化之间的联系，完成了大跨度网状结构的损伤识别研究。Wu等[8]提出一种基于应变模态构造的模态应变能损伤定位方法，推导了梁结构应变模态与位移模态之间的转换关系，建立模态应变能的应变模态表达式。数值仿真和实验研究结构均表明，该方法可以准确识别损伤位置，且比基于位移模态的模态应变能损伤识别方法具有更好的抗噪性。

由于振型的转角自由度信息难以通过实测准确获取，而常用振型扩充方法在由实测位移振型估计转角振型中会带来较大误差。笔者在Wu等[8]提出的基于应变模态的模态应变能损伤定位方法的研究基础上，基于灵敏度分析方法，推导了基于应变模态振型的梁结构模态应变能与结构损伤之间的定量关系，构造了损伤识别方程组，完成了结构损伤的定量识别。

1 基于模态应变能的损伤识别理论

1.1 基于位移模态的损伤方程组

定义损伤前后第i个单元、第j阶模态应变能[4](model strain energy，简称MSE)分别为

(1a)

(1b)

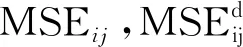
结构发生损伤后，结构模型会发生变化，对结构刚度影响显著。引入单元刚度折减系数αi描述第i个单元的损伤程度，即

(2)

令βi=1-αi，损伤前后单元刚度变化量可表示为

(3)

其中：βi为第i个单元的损伤量。

由单元模态应变能与单元刚度折减系数之间的关系[9]，建立结构损伤程度与结构模态应变能变化关系的方程组

SN×N×MβN×M=(ΔR)N×M

(4)

其中：N为单元个数；M为模态阶数；S为灵敏度矩阵；β为损伤程度矩阵；ΔR为仅考虑振型变化时的损伤前后单元模态应变能变化量矩阵。

(5)

(6)

(7)

其中：M为整体质量矩阵；K为整体刚度矩阵；Ki，Kk分别为第i个和第k个单元刚度矩阵对整体刚度矩阵的贡献，其维数与总刚度矩阵一致，除第i个和第k个单元对应自由度以外，其他位置元素的值均为零；Φj为结构的第j阶质量归一化振型；λj为第j阶固有频率。

1.2 应变模态与位移模态之间的关系

结构在发生小变形情况下，应变ε与非刚体位移u的关系可表示为

ε=ATu

(8)

AT为两者之间的关系矩阵，则有

u=Hsε

(9)

其中：Hs为位移与应变之间的转换矩阵，且

Hs=A(ATA)-1

(10)

单元位移模态振型φe与应变模态振型εe之间的关系[10]可以类似表示为

φe=Hsεe

(11)

由式(11)可知，实测应变模态与位移模态之间存在直接联系，且应变信号中包含了转角信息。引入整体位移振型与应变振型之间的转换矩阵H，即

(12)

获得第j阶结构位移模态振型Φj与应变模态振型εj的关系为

Φj=Hεjj=1,2,…,M

(13)

1.3 基于应变模态的结构损伤识别方程组

将式(11)代入式(1)，得到基于应变模态的第i个单元第j阶模态的单元模态应变能表达式为

(14)

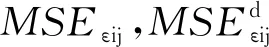
(15)

式(7)可以重新表示为

(16)

推得基于应变模态的结构损伤识别方程为

(Sε)N×N×M(βε)N×M=(ΔRε)N×M

(17)

其中：Sε为基于应变模态的灵敏度矩阵；βε为基于应变模态的损伤程度矩阵；ΔRε为基于应变模态的模态应变能变化量矩阵。

(18)

(19)

其中：εj为结构的第j阶应变模态振型。

1.4 损伤识别方程组求解

结构常发生局部损伤，引起结构有限元模型中个别单元的刚度降低，此时式(17)中的灵敏度系数矩阵Sε会呈现病态。当实测模态数据存在噪声污染时，用直接求逆的方法求解结构损伤识别方程组会带来很大误差，需要使用正则化方法提高求解的精度。笔者采用奇异值截断算法(truncated singular value decomposition，简称TSVD)[11-12]来减小噪声污染对损伤识别结果的影响，以提高求解精度。由于表示损伤程度β值不可能为负，采用非负最小二乘法[13]求解奇异值分解后的损伤识别方程。

2 数值仿真

以如图1所示，两端固支的等截面均质弹性梁为研究对象。梁的参数如下：长×宽×高=880 mm×25 mm×5 mm，分8个平面梁单元；弹性模量E=72 GPa，泊松比μ=0.3，密度ρ=2 700 kg/m3。在Wu等[8]提出的基于应变模态的模态应变能损伤定位方法的研究基础上，运用笔者提出的损伤识别理论，由损伤前后梁的应变模态定位损伤来识别各单元的损伤程度，其中损伤量以比例系数的形式给出，为无量纲量。

图1 梁结构有限元模型Fig.1 Finite element model of beam structure

当结构发生裂纹损伤时，其抗弯刚度会降低，而结构整体质量变化很小，因此笔者只考虑了损伤引起的刚度变化。在有限元仿真中，通过降低单元的抗弯刚度来模拟损伤。表1为各损伤工况对应的损伤位置和损伤程度。研究发现[9]，单元的低阶模态应变能比高阶模态应变能更好地反应结构损伤，且抗噪性能更强。因此，笔者只研究基于前三阶模态应变能的损伤指标。

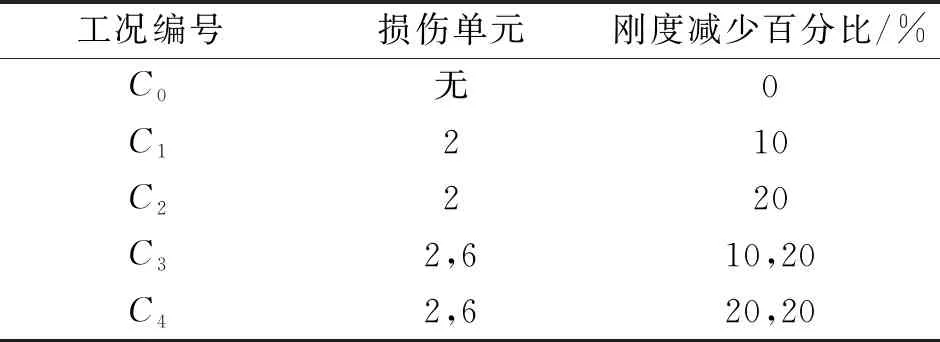
表1 梁模型各损伤工况

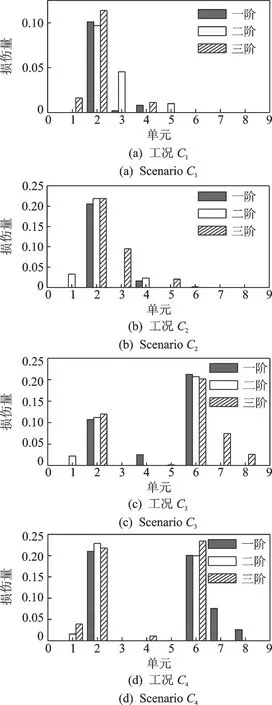
图2 无噪声干扰下基于前三阶应变模态的损伤识别结果Fig.2 Damage identification results based on the first three strain modes without noise pollution

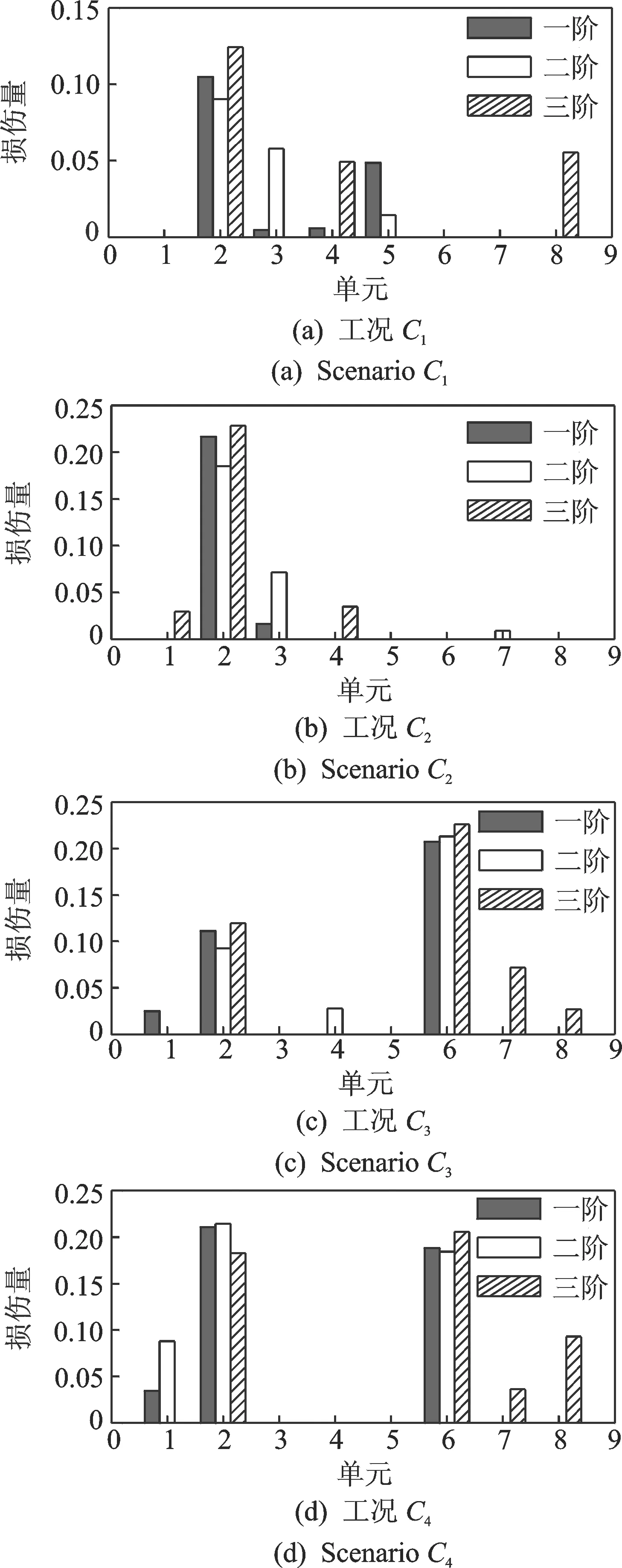
图3 5%噪声干扰下基于前三阶应变模态的损伤识别结果Fig.3 Damage identification results based on the first three strain modes with 5% noise pollution

为了说明该方法的有效性，笔者研究了多种损伤工况下梁模型的损伤识别效果。为了贴近工程实际，研究了噪声干扰对结构损伤识别结果的影响。从图2(a)，2(b)和3(a)，3(b)可以看出，对于不同损伤程度的单损伤工况，在有无噪声干扰的情况下，该方法均可以有效识别出损伤位置和损伤程度。同样的，从图2(c)，2(d)和3(c)，3(d)可以发现，对于多损伤工况，该方法依然有效。为了进一步说明损伤识别效果，并考虑到结构发生小损伤后，即使识别结果与真实值存在微小的差异都会使损伤指标的百分比误差很大，影响对结果准确度的判断。因此，笔者以单元刚度折减系数作为识别结果误差的表征。表2中各损伤工况的识别结果表明，无论有无噪声干扰，采用本研究方法，识别误差均可控制在5%以内，识别结果可靠。同时发现，基于第1阶应变模态振型的识别结果精度高于基于第2, 3阶模态识别结果精度，这与文献[9]中得出采用低阶模态应变能可以更好地获取损伤识别结果的结论一致。因此，本研究方法适用于多种损伤工况，且损伤识别结果可靠，同时具有良好的抗噪性。

为了进一步揭示本研究方法在抗噪声方面的优势，将笔者提出的基于应变模态的结构损伤识别(方法I)与基于传统位移模态和振型扩充法[5]的结构损伤识别(方法II)进行对比分析。同样采用图1中梁模型为研究对象，以单损伤工况C2和多损伤工况C3为例，采用基于第1阶模态的损伤指标，对比无噪声和5%噪声情况下两种方法的损伤识别结果如图4，5所示。

从图4可以发现，在无噪声干扰的情况下，无论是单损伤还是多损伤，方法Ⅰ和方法II均可以有效识别出损伤位置和损伤程度，且损伤识别结果无明显差异。图5表明，在有噪声干扰的情况下，方法Ⅰ与方法Ⅱ的损伤量识别结果出现了较为明显的差异。对于发生损伤的梁单元，方法Ⅰ的识别结果比方法Ⅱ的识别结果更加准确； 而对于未发生损伤的梁单元，方法Ⅱ的识别结果与真实值出现了较为明显的偏差。例如：工况C2中的第4个单元损伤量超过5%；工况C3中的第4个单元损伤量高于第2个单元损伤量。同时，表3的结果也表明，在无噪声干扰的情况下，方法Ⅰ与方法Ⅱ的损伤识别结果无明显差异，误差均控制在2%以内；但在噪声干扰的情况下，方法Ⅱ的损伤识别结果误差明显高于方法I的损伤识别结果误差，其中工况C2的损伤识别结果误差超过5%。因此， 方法Ⅰ比方法Ⅱ的抗噪性能更强，损伤识别结果更为可靠。

表2各工况下损伤单元的刚度折减系数α识别结果

Tab.2Theidentifiedstiffnessreductionfactorsαofthedamagedelementsunderdifferentdamagescenarios

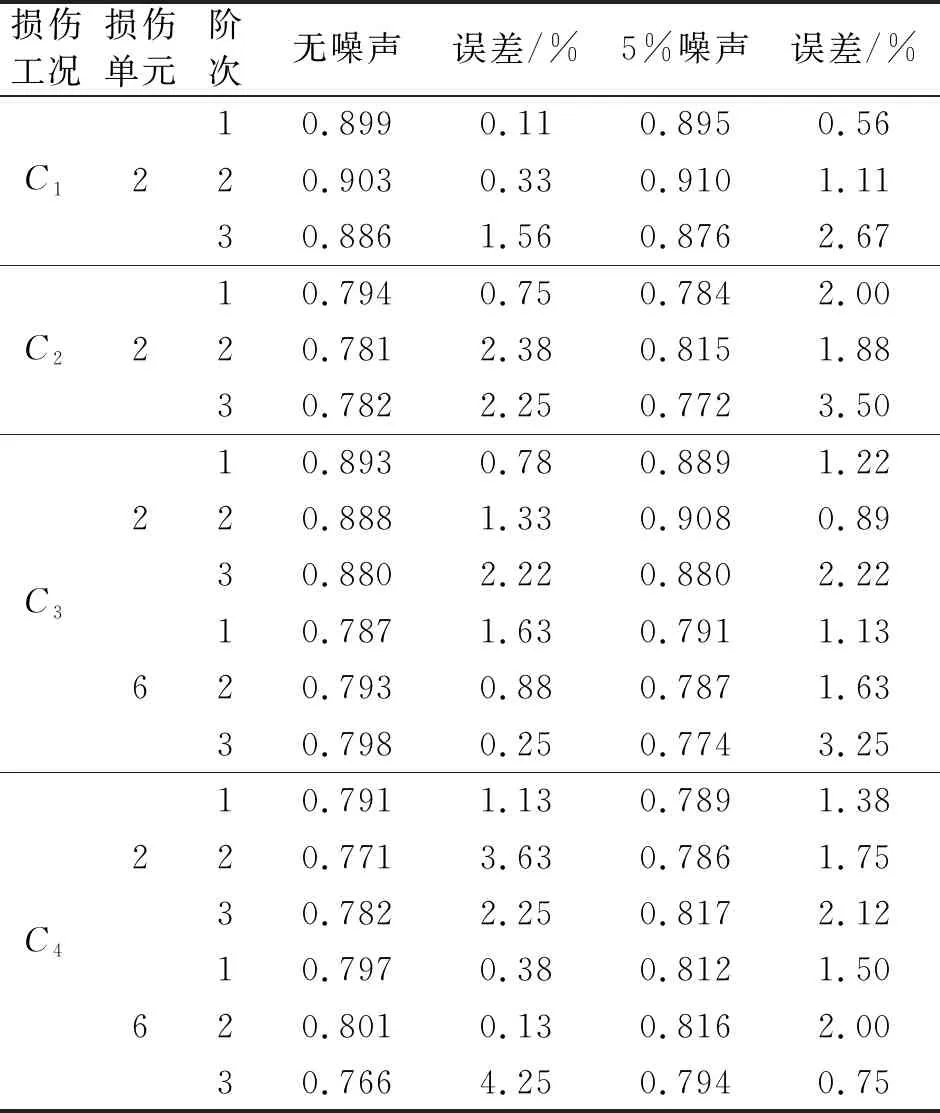
损伤工况损伤单元阶次无噪声误差/%5%噪声误差/%C1210.8990.110.8950.5620.9030.330.9101.1130.8861.560.8762.67C2210.7940.750.7842.0020.7812.380.8151.8830.7822.250.7723.50C32610.8930.780.8891.2220.8881.330.9080.8930.8802.220.8802.2210.7871.630.7911.1320.7930.880.7871.6330.7980.250.7743.25C42610.7911.130.7891.3820.7713.630.7861.7530.7822.250.8172.1210.7970.380.8121.5020.8010.130.8162.0030.7664.250.7940.75

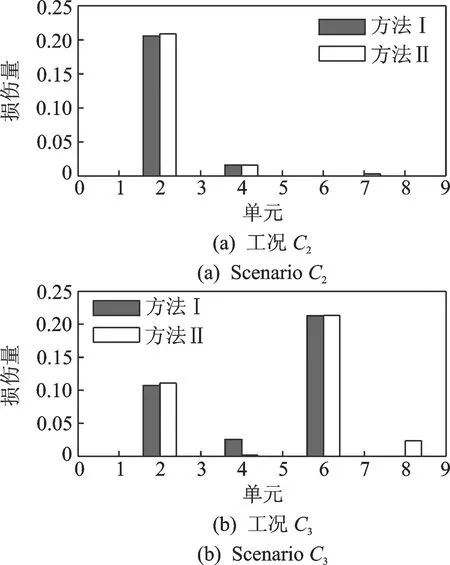
图4 无噪声干扰下方法Ⅰ，Ⅱ的损伤识别结果对比Fig.4 Comparison between the damage identification results from method Ⅰ and method Ⅱ without noise pollution

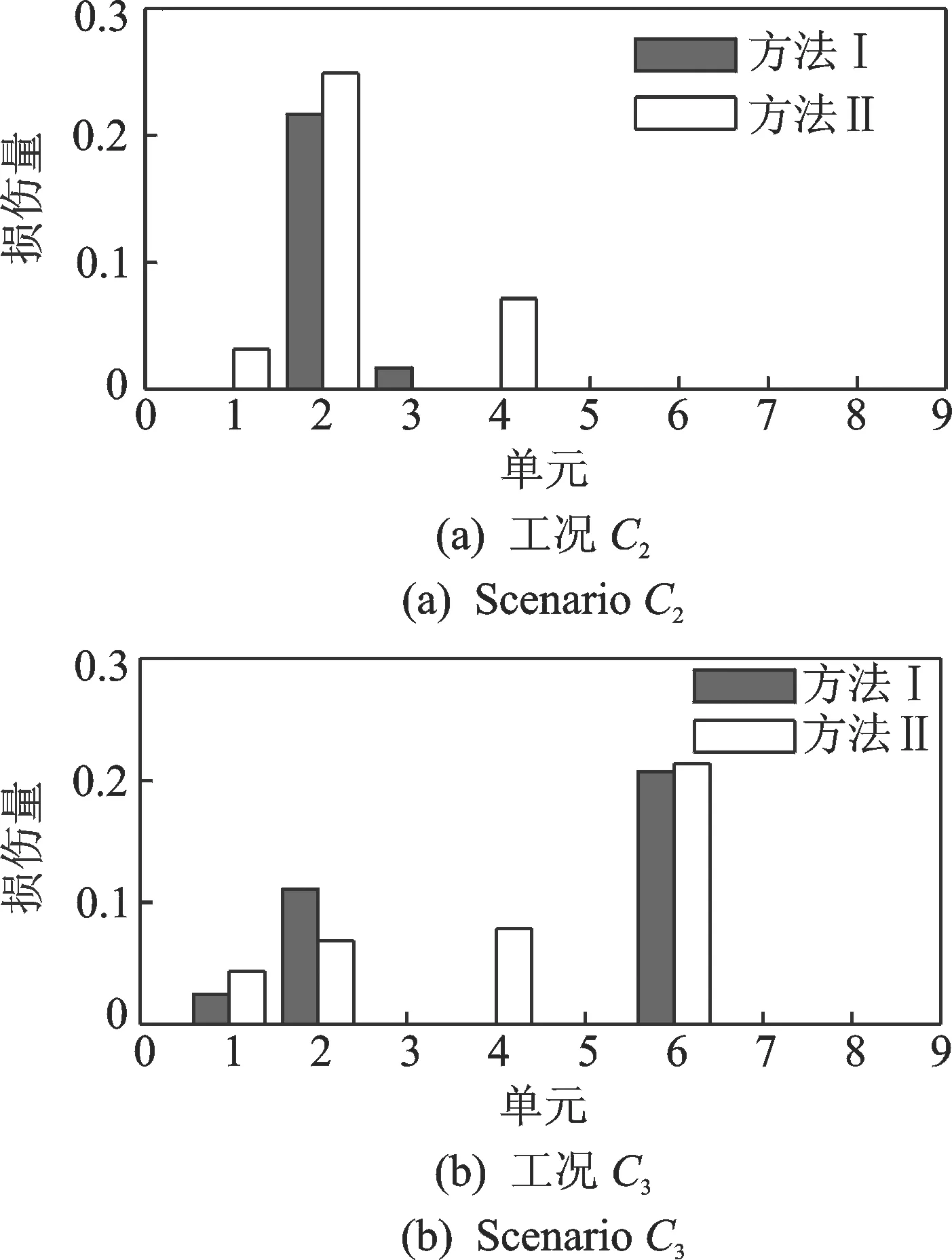
图5 5%噪声干扰下方法Ⅰ，Ⅱ的损伤识别结果对比Fig.5 Comparison between the damage identification results from method Ⅰ and method Ⅱ with 5% noise pollution

表3方法Ⅰ，Ⅱ中各工况损伤单元的刚度折减系数α识别结果

Tab.3TheidentifiedstiffnessreductionfactorsαofthedamagedelementsfrommethodⅠandmethodⅡ

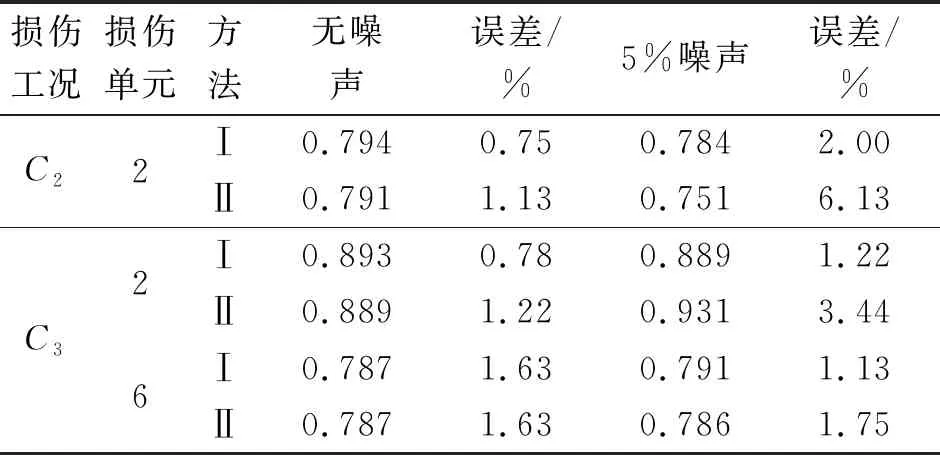
损伤工况损伤单元方法无噪声误差/%5%噪声误差/%C22Ⅰ0.7940.750.7842.00Ⅱ0.7911.130.7516.13C326Ⅰ0.8930.780.8891.22Ⅱ0.8891.220.9313.44Ⅰ0.7871.630.7911.13Ⅱ0.7871.630.7861.75

3 实 验

图6 模态实验系统与单元损伤模拟Fig.6 Modal testing system and elemental damage simulation

以图1所示的两端固支的等截面均质弹性梁为实验研究对象，其材料参数如上所述。如图6(a)所示，在节点6处布置加速度传感器识别位移模态，采用力锤激励的方法识别模态信息。图6(b)中，在每个节点上布置光纤布拉格光栅传感器，采用基于随机子空间算法识别应变模态[14-15]。需要说明的是，采用其他的模态识别方法其识别结果与该方法存在一定差异，篇幅限制，对此未做深入研究。笔者通过在梁局部制造断口模拟损伤，由于该模型中单元损伤程度与截面宽度成正比，由此可以由断口大小模拟定量损伤。实验中开展了对单损伤工况C2和多损伤工况C4的损伤识别研究。

理论上应变模态与位移模态对应频率是相同的，表4给出的各损伤工况下位移模态与应变模态前三阶固有频率的结果表明，位移模态频率和应变模态频率之间的差异均可控制在5%以内。由于两个实验在系统搭建和识别方法上均不相同，且识别误差的来源多样，无法断定误差主要来自信号测量或者是识别方法。5%以内的误差在当前的实验条件下保证了一定的精确度。图7和图8分别为前三阶位移模态和应变模态的实测振型。

表4各损伤工况下位移模态与应变模态前三阶固有频率比较

Tab.4Modalfrequenciesofthebeamfromtwosetsofexperimentaltests

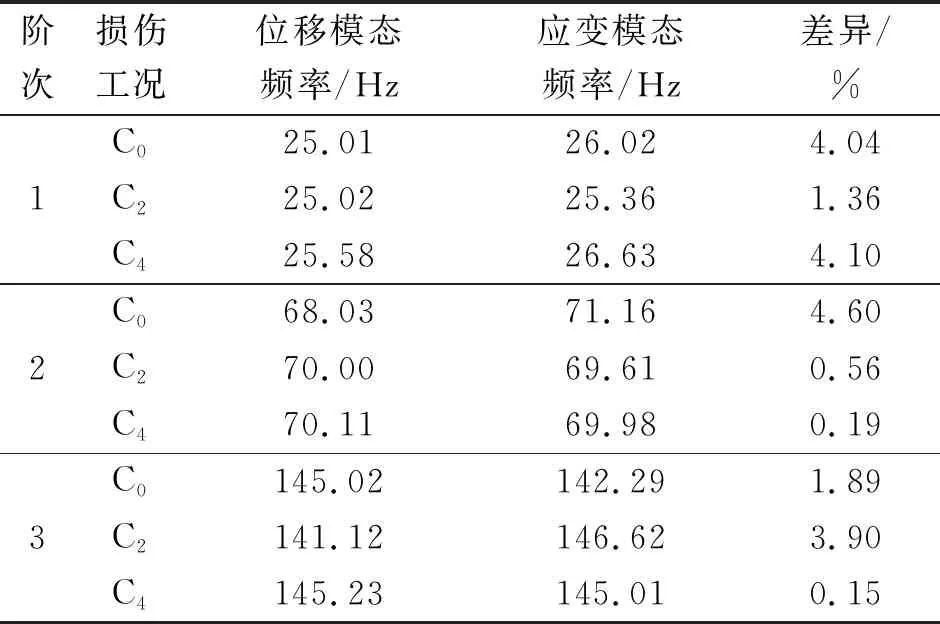
阶次损伤工况位移模态频率/Hz应变模态频率/Hz差异/%1C025.0126.024.04C225.0225.361.36C425.5826.634.102C068.0371.164.60C270.0069.610.56C470.1169.980.193C0145.02142.291.89C2141.12146.623.90C4145.23145.010.15

图9表明，无论是单损伤工况还是多损伤工况，方法Ⅰ均可有效识别出损伤位置和损伤程度。表5中损伤工况C2，C4的识别结果说明，采用本研究方法，识别误差均可控制在较小的范围之内，损伤识别结果是可靠的。同时发现，基于第1阶应变模态振型的识别结果误差均控制在5%以内，比基于第2, 3阶应变模态识别结果精度更加稳定和准确。 从图10发现，无论是单损伤还是多损伤，方法Ⅱ均无法有效识别出损伤位置和损伤程度， 其损伤识别结果不准确。实验研究与数值仿真结论一致。在实验验证过程中，笔者使用了较多测点，针对测点数可能对识别结果的精度产生影响而开展了研究，鉴于篇幅限制，在此直接给出了研究结论：测量点数的减少，会使损伤识别误差增加，如测量点未覆盖损伤所在区域，损伤识别结果会呈现更大误差。在实际工程应用中，可以通过仿真分析预测结构易损部位，通过增加易损部位周围的测量点数布置，提高损伤识别的精度。

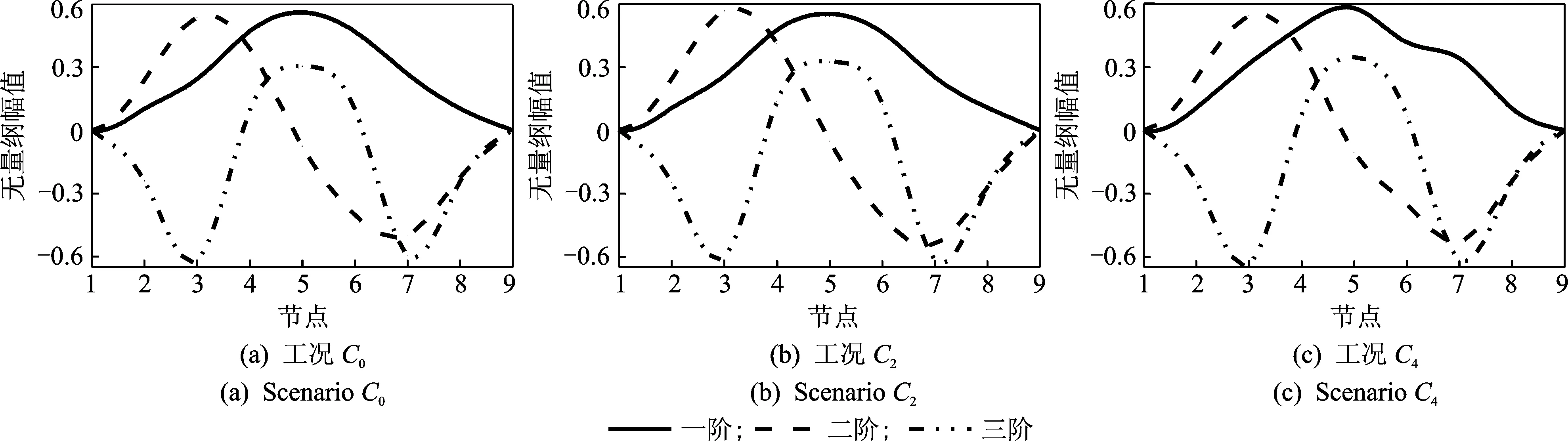
图7 各损伤工况下梁的前三阶实测位移振型Fig.7 The first three measured displacement modes of beam under different damage scenarios

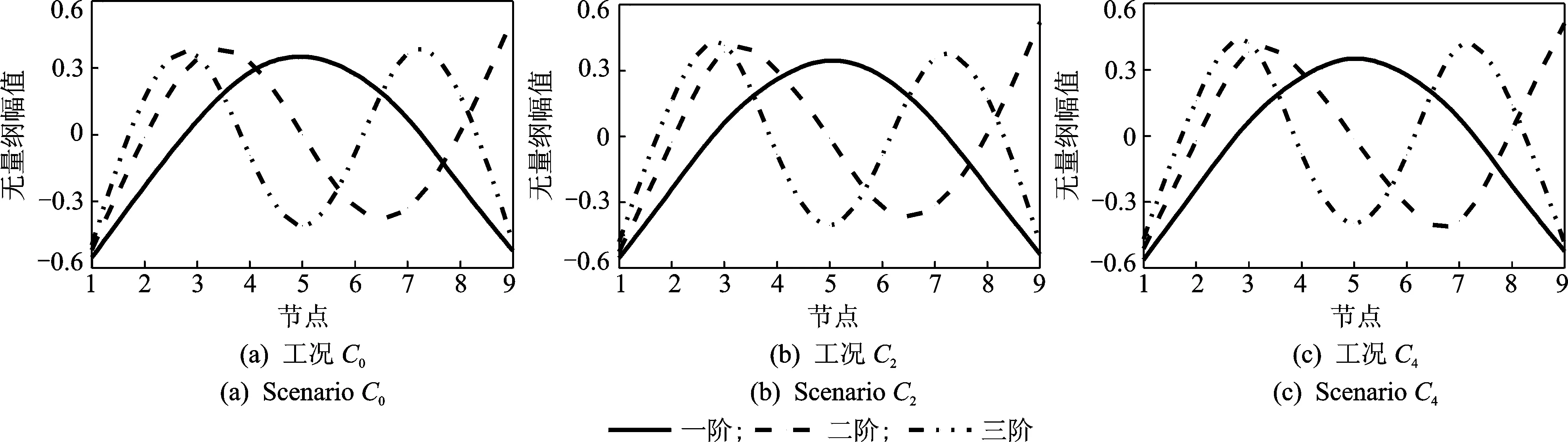
图8 各损伤工况下梁的前三阶实测应变振型Fig.8 The first three measured strain modes of beam under different damage scenarios

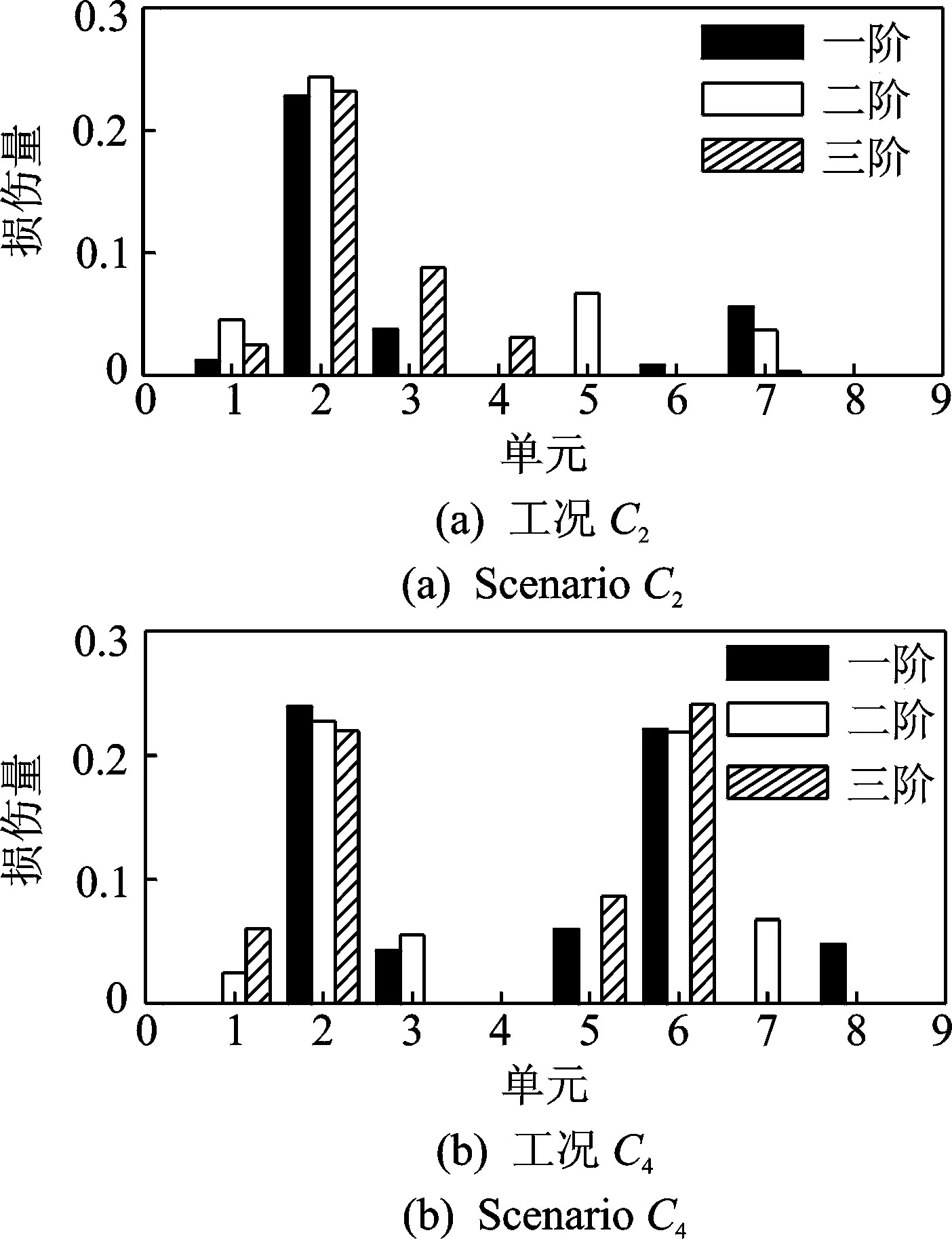
图9 方法Ⅰ中基于前三阶实测应变模态的损伤识别结果Fig.9 Damage identification results based on the first three measurement strain modes using method Ⅰ

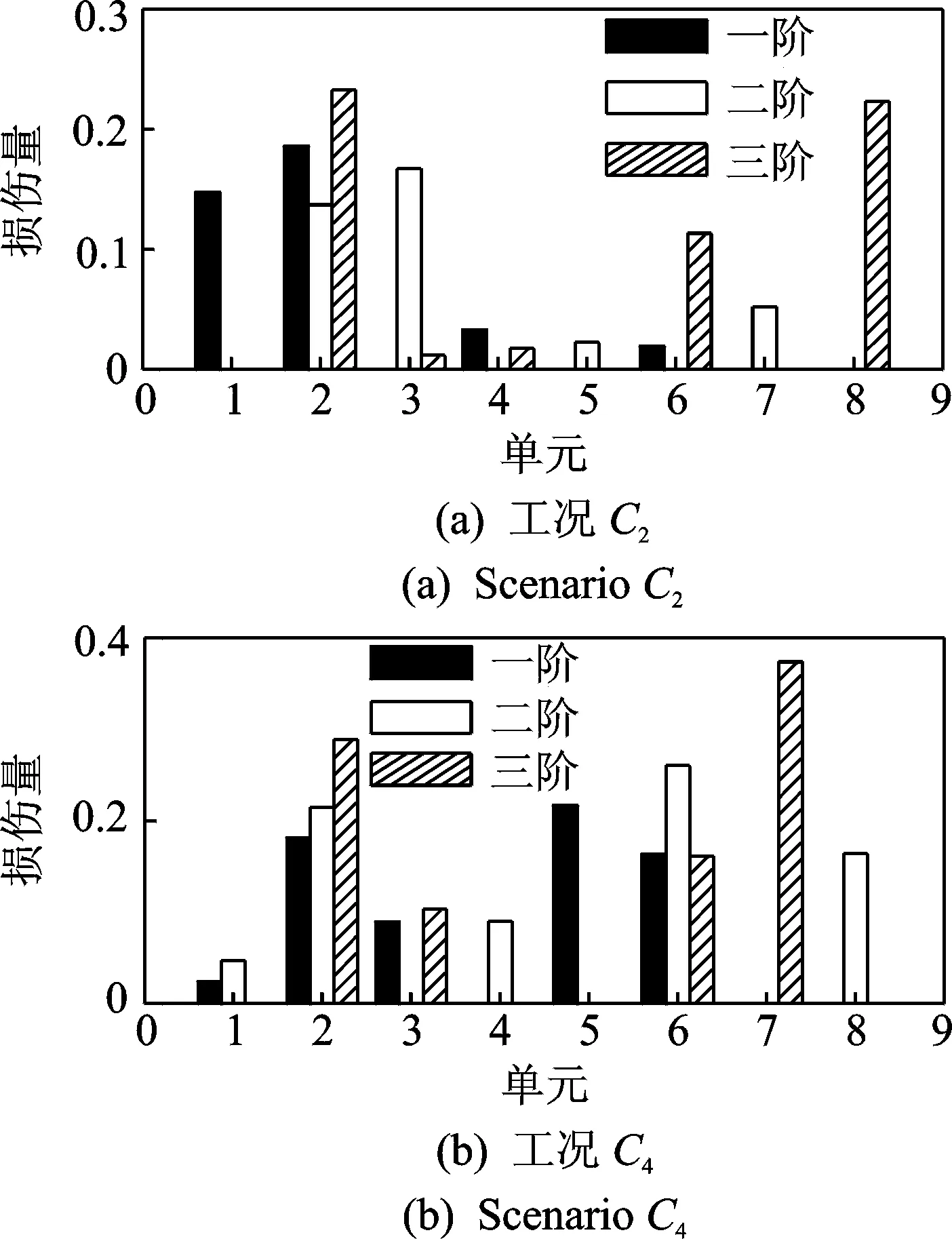
图10 方法Ⅱ中基于前三阶实测位移模态的损伤识别结果Fig.10 Damage identification results based on the first three measurement displacement modes using method Ⅱ

表5基于实测数据和方法Ⅰ的刚度折减系数α识别结果

Tab.5IdentifiedstiffnessreductionfactorsαbasedonmeasurementdatausingmethodⅠ

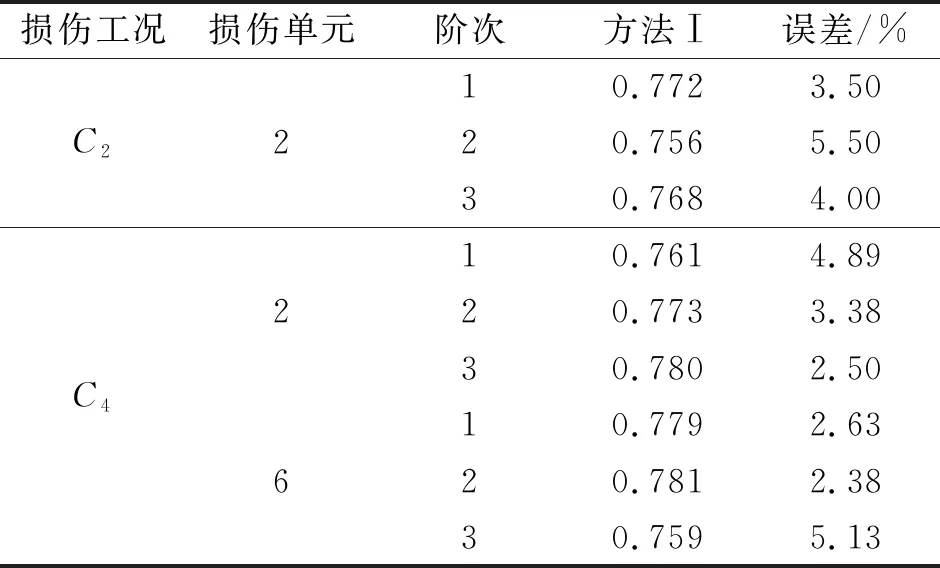
损伤工况损伤单元阶次方法Ⅰ误差/%C2210.7723.5020.7565.5030.7684.00C42610.7614.8920.7733.3830.7802.5010.7792.6320.7812.3830.7595.13

4 结束语

笔者将传统采用位移模态的单元模态应变能表达式用基于应变模态的表达式替换,推导了损伤识别方程组，发展了基于应变模态的单元模态应变能结构损伤识别方法，实现了结构损伤的准确定位和定量。仿真分析和实验研究结果均表明，相比于传统的基于位移模态和振型扩充法的结构损伤识别法，该方法避免了基于含噪声污染信号的振型扩充法带来的较大误差，提高了损伤识别算法的抗噪能力和识别精度。采用基于第1阶应变模态数据的损伤识别效果更优于采用高阶模态的损伤识别效果。该方法易于实施，在工程损伤识别中具有很好的应用前景。