基于信息熵与Lempel-Ziv的拧紧设备性能评估方法*

范国良, 李爱平, 刘雪梅, 顾佳巍, 徐立云

(同济大学机械与能源工程学院 上海，201804)

引 言

对于制造企业而言，机械设备的性能不稳定性、故障突发性及随机性是研究的重点和难点，不仅关系到生产成本与产品质量，更会对工作人员造成安全威胁[1]。机械设备性能退化过程具有的不均匀性、差异性、多样性和随机性等特点，以及日益加深的复杂化、柔性化和智能化都给设备性能评估提出了更高的挑战。

随着生产系统化的加强，关键设备的状态监测与性能评估能够保障生产过程的稳定有序进行。周丰旭等[2]针对可修制造系统在维修过程中呈现出的性能多态性，提出了基于性能衰退过程的多状态可靠性建模方法，探讨了系统因老化导致性能衰退过程的可靠度分析方法。Li等[3]考虑工作条件对可靠性的影响，基于Cox比例风险模型提出数控机床可靠性评估模型，用以描述工作条件协变量和数控机床可靠性水平之间的数学关系。Lad等[4]基于生命周期成本、设备可用度和设备整体有效度建立数控磨床可靠性评价模型，为机床最佳配置选择和设备维护提供理论指导。Sadok等[5]考虑设备性能退化研究再制造系统，采用模拟随机流体模型研究系统的性能评估，优化机器退化成本和最优库存成本。旋转轴类系统作为多数设备的关键工作子系统，黄海凤等[6]对数控机床主轴系统进行性能退化程度分析，采用动态模糊神经网络方法，融合振动信号、电流信号和声发射信号训练评估模型。针对摩擦提升机的主轴系统，董磊等[7]提出一种基于复杂网络聚类的故障诊断方法，解决主轴系统故障耦合、特征微弱等问题。

以可靠性为代表的设备性能评估方法以故障率为评价指标，一定程度上能够反映设备故障对整机性能的影响程度，而设备在正常工作状态下表现出的性能退化也会造成产品质量的波动。以正常工作状态下生产质量数据对机械设备性能进行评估，能够对设备状态进行预判，为预知性维护策略制定提供依据，保证设备高性能稳定生产。

复杂性理论是刻画随机性和不确定性的有效手段，为机械设备性能评估提供了新的思路。用以定量表达复杂性的数学方法主要有信息熵、柯尔莫哥洛夫熵、李雅普诺夫指数和Lempel-Ziv算法等[8]。Efthymiou等[9]应用Lempel-Ziv算法测度制造系统的不可预测性，并以此研究了制造性能指标的波动情况。董新峰等[10]针对磨削加工中的颤振现象，提出一种基于经验模式分解复杂度与鉴别信息的颤振预测方法，对磨削加工颤振进行预测。另外，以磨床主轴为分析对象，采用Lempel-Ziv指标对磨床主轴状态进行劣化水平判断[11]。Pan等[12]通过相关维数和近似熵对滚动轴承的退化程度进行复杂性分析，以评估其退化水平。Fan等[13]基于柯尔莫哥洛夫熵建立拧紧机性能评估模型，以测度其性能退化趋势。

以复杂性分析为手段，对系统、设备及关键部件，尤其对主轴等旋转轴类子系统进行的状态分析和性能评估是近年比较新颖和有效的尝试，能够量化系统运行过程中状态的不确定性和随机性，但多以单一复杂度指标进行性能判定，对于退化过程中性能指标表现出的复杂性特征差异尚不能区分。性能指标不同维度的复杂性特征差异恰恰为更准确评估和反映设备的退化状况提供了有效的研究思路。

笔者以自动化装配线中的自动拧紧设备为对象，从实时运行状态出发，结合信息熵和Lempel-Ziv算法，提出设备性能复杂性随机波动程度和状态无序程度两个维度的复杂性测度方法。以设备正常运行阶段的过程质量数据测算设备运行的性能复杂度，实现拧紧设备性能的综合评估。区分并应用过程质量数据表现出的不同维度的设备退化特征，与单一指标的复杂性测度方法相比,能够更准确评估其退化水平。另外，在正常工作状态下进行的性能评估与从故障角度进行研究相比，能够在故障发生前对设备进行合理预判。

1 拧紧设备性能复杂性测度方法

衡量拧紧设备性能的关键指标是拧紧扭矩和拧紧角度，其直接关系到产品的装配质量。在工作过程中，随使用时间和拧紧次数增加，设备性能会出现退化，表现为扭矩和角度值出现波动，且波动的范围逐渐扩大，精确度下降等，直接导致装配质量的不稳定。基于复杂性测度的拧紧设备性能评估问题可以描述为：拧紧设备的性能由一系列性能指标所表征，已知拧紧设备监测到的一段时间序列数据，建立性能复杂性测度模型来评估拧紧设备的性能随时间变化的规律。

1.1 基于信息熵的拧紧设备复杂性测度

复杂性是指系统难以被理解、描述、预测和控制的状态[14-15]。复杂度是对系统复杂性更精确的定义以致定量化的刻画。从信息论的角度，基于信息熵的复杂性测度是与状态和概率紧密联系的，用以描述系统所预期可能的状态所需要的信息量。

1.1.1 拧紧设备性能指标状态划分

针对拧紧设备，可以根据设备的运行状态指标，如加工质量及装配精度来定义设备状态。选取一定时间段的拧紧数据作为样本进行相关状态的特征分组和标定。选取的样本区间均为有效合格数据，一旦出现故障数据则认定设备故障，无需进行测度，最终选取扭矩和角度作为性能指标。区别于使用故障率等指标衡量设备性能状况时只能从设备是否正常运行角度判定的局限，以合格过程数据的波动程度和无序程度来衡量设备性能状况更能准确把握设备性能退化对拧紧质量的影响程度。

设拧紧设备设定的扭矩输出值为Fs，扭矩输出的上限和下限分别为Fu和Fb，可以选取合适的跨度值b限定状态范围，并且可以根据扭矩输出上下限Fu和Fb，结合扭矩输出标定值Fs的大小得出设备在动态运行中的状态Sm，状态数为m，当某一个扭矩测量值为Fi时，可以按照以下规则对其进行标定。

(1)

其中：Sm以涵盖上下限值或涵盖样本数据的最大最小值为准。

1.1.2 拧紧设备性能复杂度模型

已知离散信息源可用一维离散型随机变量来描述，记为X，取值于符号集{x1,x2,…,xi,…,xn}，其中n为正整数，若信息源X输出xi的概率服从概率分布p(xi)，则信息熵H(X)定义[16]为

(2)

如果X表示一个系统，xi和p(xi),(i=1,2,…,n)为该系统n个可能的状态及各状态发生的概率，则H(X)为系统的信息熵，即描述系统X时所需要的信息量。H(X)表示系统X的不确定性大小，信息熵越大，系统不确定性越大[15]。

将设备的可能状态进行标定后，对所测得数据进行下一步复杂性测度。首先，将样本时间按照一定间隔划分为单位时间，对单位时间的复杂性进行测度计算；然后，测算出整个样本时间T内单位时间Δt间隔下复杂度的变化趋势。

第k个单位时间内，可以得到该时间段测量数据总数量为Nk，并对其进行状态标定，分别归属于Sm的各个区间，统计各个区间内的频次，可以得到各个状态在单位时间内的概率分布，即

pj=nj/Nk

(3)

其中：pj为设备处于状态j的概率；nj为设备在该单位时间内处于状态j的统计频次；Nk为设备在第k个单位时间内的测量数据总频次。

设某制造设备在实际运行中拥有的状态数为m，且各个状态之间相互独立，分别为S1,S2,…,Sn,…,Sm。第k单位时间内设备的动态复杂度可根据下式计算

(4)

其中：pj为设备处于状态j的概率，pj>0；1≤j≤m为有可能不出现所有预设的状态；对于概率为0的状态，即没有出现的状态不予计算；k为采样时间段内的单位时间序列编号。

从信息论的角度看，性能复杂度模型是通过描述拧紧设备的状态变化的复杂度来刻画其在运行过程中性能状态的退化程度。基于状态概率分布计算得到的性能复杂度模型，反映了设备状态可能分布的复杂状况，测算了设备状态的离散程度。对于状态之间变化的速率，即设备状态的无序程度，则依靠Lempel-Ziv算法来反映设备性能复杂度的另一个维度特性。

1.2 基于Lempel-Ziv算法的拧紧设备复杂性测度

Lempel-Ziv算法用符号序列表示动力系统(或测量得到的时间序列)，以便对动力系统进行算法复杂度的计算。信息熵从统计意义出发，难于表达系统的内在结构本质。Lempel-Ziv算法则不同，强调系统的复杂程度与该系统行为的最小描述量有关。

1.2.1 性能指标粗粒化

设拧紧设备的拧紧性能指标数据为时间序列F={F1,F2,…,FM}，M为单位时间内样本数量，粗粒化就是将其重构为[0,1]序列S={s1,s2,…,sm,…,sM}，以便计算相应的复杂度。

序列F的平均值为

(5)

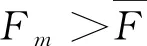
1.2.2 拧紧设备复杂性测度

基于Lempel-Ziv算法计算序列F={F1,F2,…,FM}的复杂度，具体流程如图1所示，步骤如下：

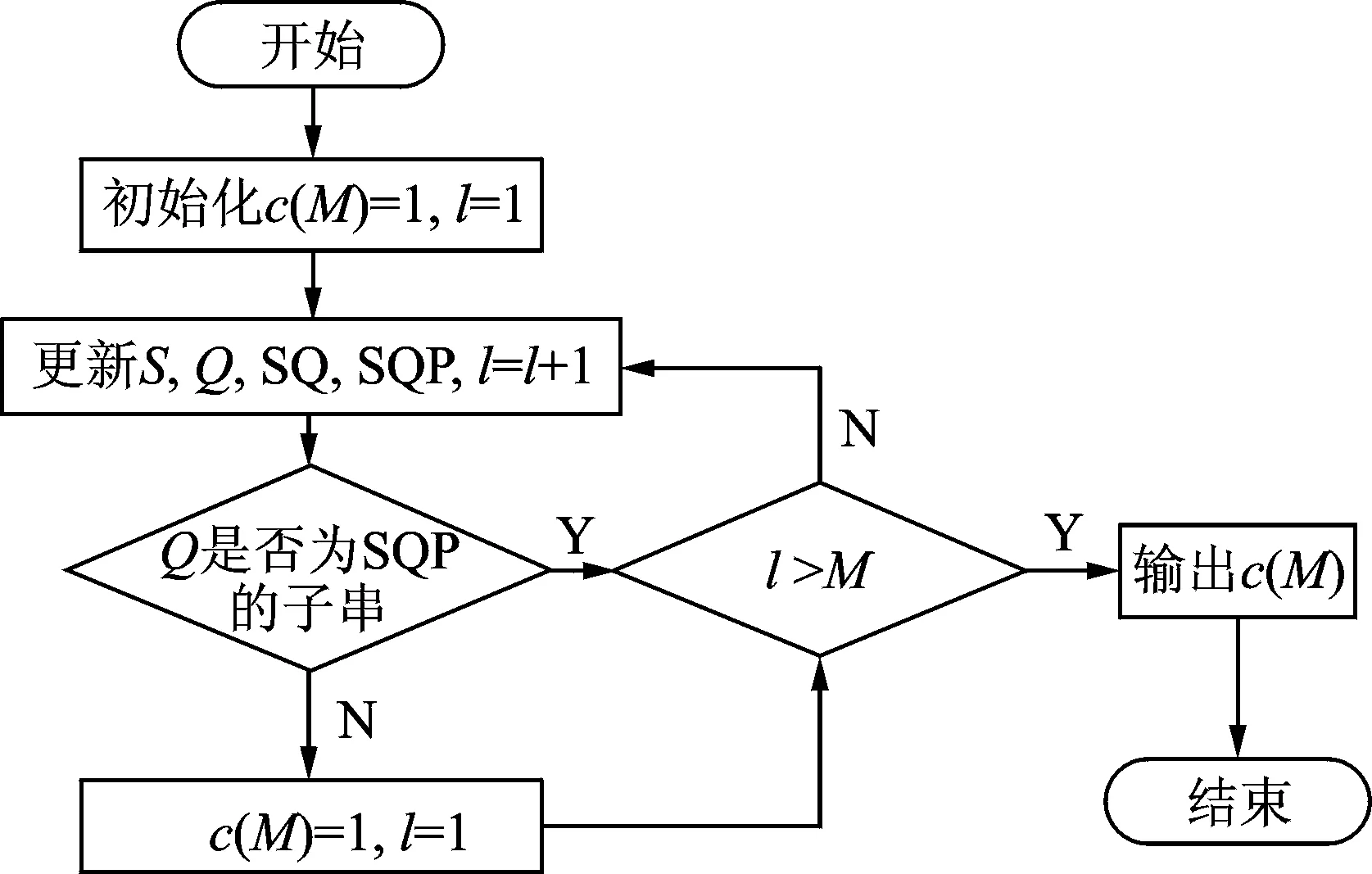
图1 Lempel-Ziv算法流程图Fig.1 Algorithm flowchart of Lempel-Ziv

1) 初始化c(M)=1，构造S，Q序列，S和Q代表序列F的两个子序列；

2) 构造SQ，SQP序列，SQ为Q排在S后面由S和Q组成的序列，SQP为SQ去掉最后一个元素后的序列，设S={s1,s2,…,sl}，Q={sl+1}，SQP={s1,s2,…,sl}；

3) 判断Q是否为SQP的子串，若是，则S不变，更新Q={sl+1,sl+2}，SQP={s1,s2,…,sl+1}；若否，则S=SQ，Q={sl+3}，且c(M)=c(M)+1；

4) 重复步骤3循环至S的最后一位为止，输出c(M)为设备Lempel-Ziv复杂度。

1.2.3 复杂度标准化

为使设备Lempel-Ziv复杂度具有可比性，对Lempel-Ziv复杂度进行标准化处理。Lempel等证明了对属于[0,1]的序列几乎所有的c(M)都会趋向于定值。序列S的长度为M，序列中不同元素的种类为α，则

(6)

其中：M→∞；εM→0；c(M)取上限。

(7)

计算标准化Lempel-Ziv复杂度

(8)

其中：cLZ(M)为反映设备复杂程度的标准化度量。

单一加工质量结果的设备复杂度应该为0，加工质量结果随机的设备复杂度最大，定义为1。

Lempel-Ziv算法侧重设备运行数据在均值附近上下波动变化的复杂程度，可以表征一个时间序列内新模式或者新变化出现的速率。通过对粗粒化序列变化的测算来衡量设备运行状态变化的复杂性。设备性能平稳或者稳定退化的情况下，Lempel-Ziv复杂度越小。反之，Lempel-Ziv复杂度增长时，设备性能趋向随机和混沌，即反映出设备性能的无序程度增加，稳定保持能力下降。

1.3 基于信息熵与Lempel-Ziv算法的拧紧设备性能复合复杂度

综合上述两个复杂性测度模型，基于状态概率分布所构建的信息熵性能复杂度模型，反映了设备状态可能分布的复杂状况，测度了设备性能的随机波动程度。Lempel-Ziv算法则侧重设备运行状态的无序程度，可以反馈设备在当前性能状态下稳定保持的能力。综合两个测度模型可以建立如下的复合复杂性测度模型CO(M)，即

CO(M)=[Ck,cLZ(M)]

(9)

(10)

将基于信息熵与Lempel-Ziv算法的复杂性测度值统一在一个向量矩阵内，两个矩阵元素分别测度了随机波动程度及状态无序程度，而复合复杂度CO(M)则可以表征设备性能的综合指标，以评价拧紧设备的综合性能。

2 实例验证

对基于信息熵和Lempel-Ziv算法的拧紧设备性能评估方法进行合理验证，选取发动机装配线上的拧紧设备进行半年的监测。上汽SGE装配线上存在多台拧紧设备，设备实物如图2所示。

图2 拧紧设备实物图Fig.2 Schematic diagram of tightening equipment

该类拧紧设备负责完成生产过程中多处拧紧作业，所有拧紧设备都带有扭矩和角度实时监测功能，能够测量所有工件的拧紧作业数据并上传到数据中心以供监测。现选取第12工位的拧紧设备的一根拧紧轴作为评估对象，因所有拧紧轴都属同一型号，所以完全可以推广到其他拧紧轴和设备。

2.1 扭矩指标复杂性测度

扭矩设定值为58 N·m ±5 N·m ，样本时间总长为115 d，每周间隔采集数据，共17 d。统计数据可知，所有的扭矩跨度区间为58～58.8 N·m ，可以将扭矩数据划分为4个状态区间：S1:58.0～58.2 N·m;S2:58.2～58.4 N·m ;S3:58.4～58.6 N·m ;S4:58.6～58.8 N·m 。将所有统计所得数据根据单位时间进行状态标定，得到测量数据的状态概率分布如表1所示。

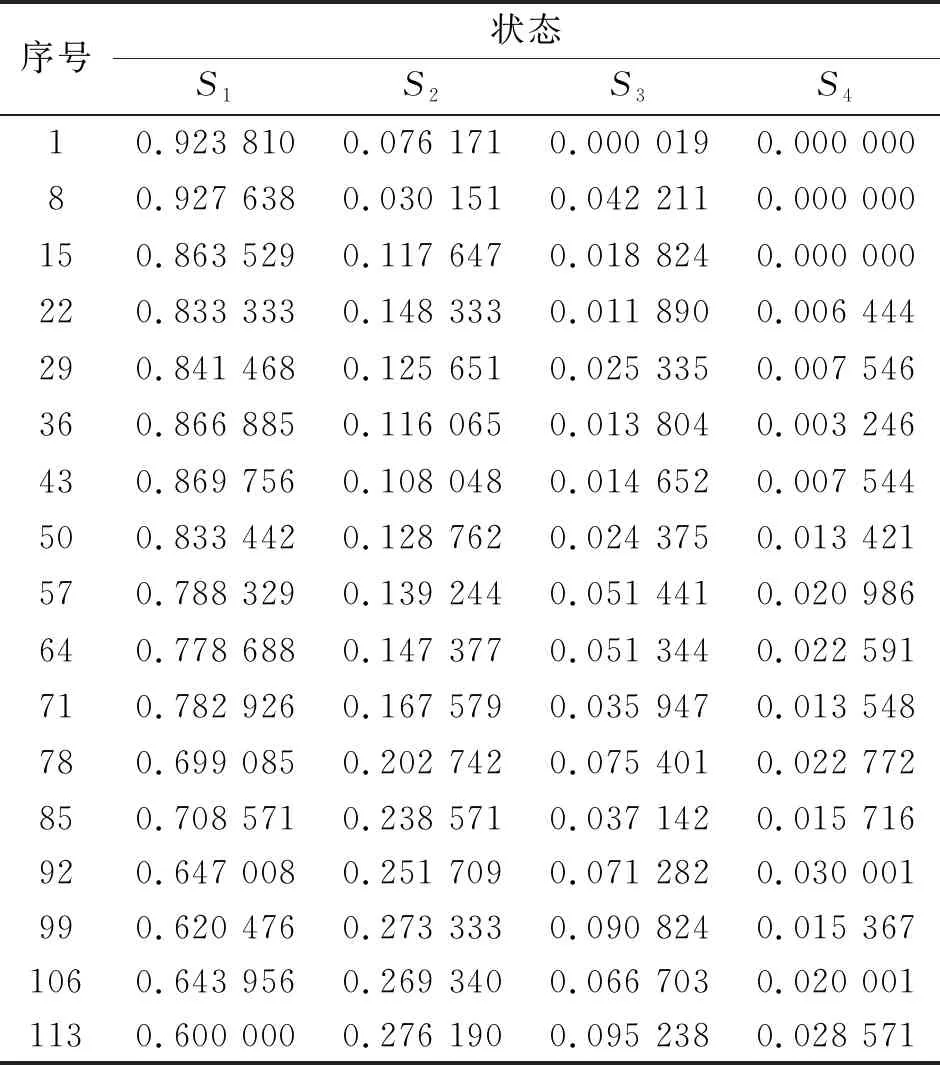
表1 样本数据扭矩状态概率分布表

根据性能复合复杂度模型计算拧紧设备在样本区间内各天的信息熵值、基于Lempel-Ziv算法的设备复杂度值及复合复杂度值。表2为设备扭矩性能复杂度计算结果。标准化过程假设序列长度为无限大，实际采集的序列不可能是无限大，有限序列的复杂度会被严重高估，甚至出现大于1的情况[17]。笔者采用的Lempel-Ziv标准化过程是对性能指标进行趋势判断，所以计算结果不作为绝对复杂度来评价，而作为相对复杂度来判断设备性能的退化趋势是正确可靠的，其中，计算的复杂度值为无量纲单位。

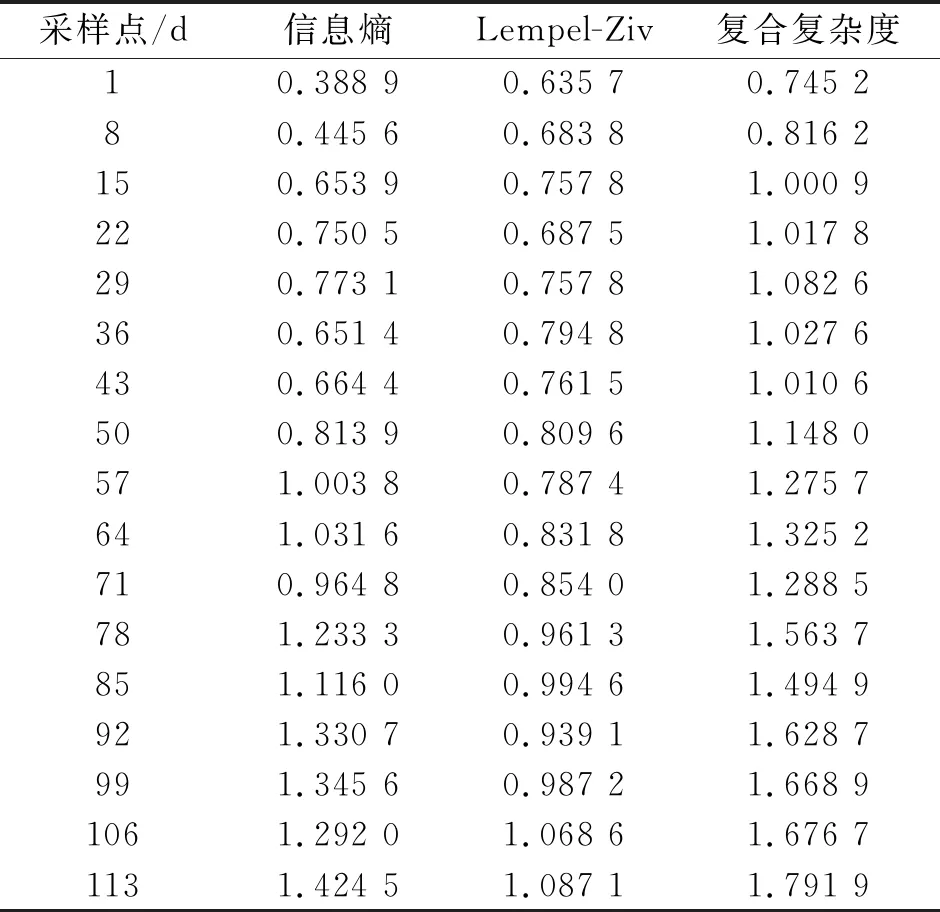
表2 设备扭矩性能复杂度计算结果

2.2 角度指标复杂性测度

角度的区间为40°～70°，将所有的角度数据划分为4个状态区间：X1:40°～47.5°;X2:47.5°～55°;X3:55°～62.5°;X4:62.5°～70°，如表3所示。计算信息熵值、Lempel-Ziv复杂度及复合复杂度如表4所示。

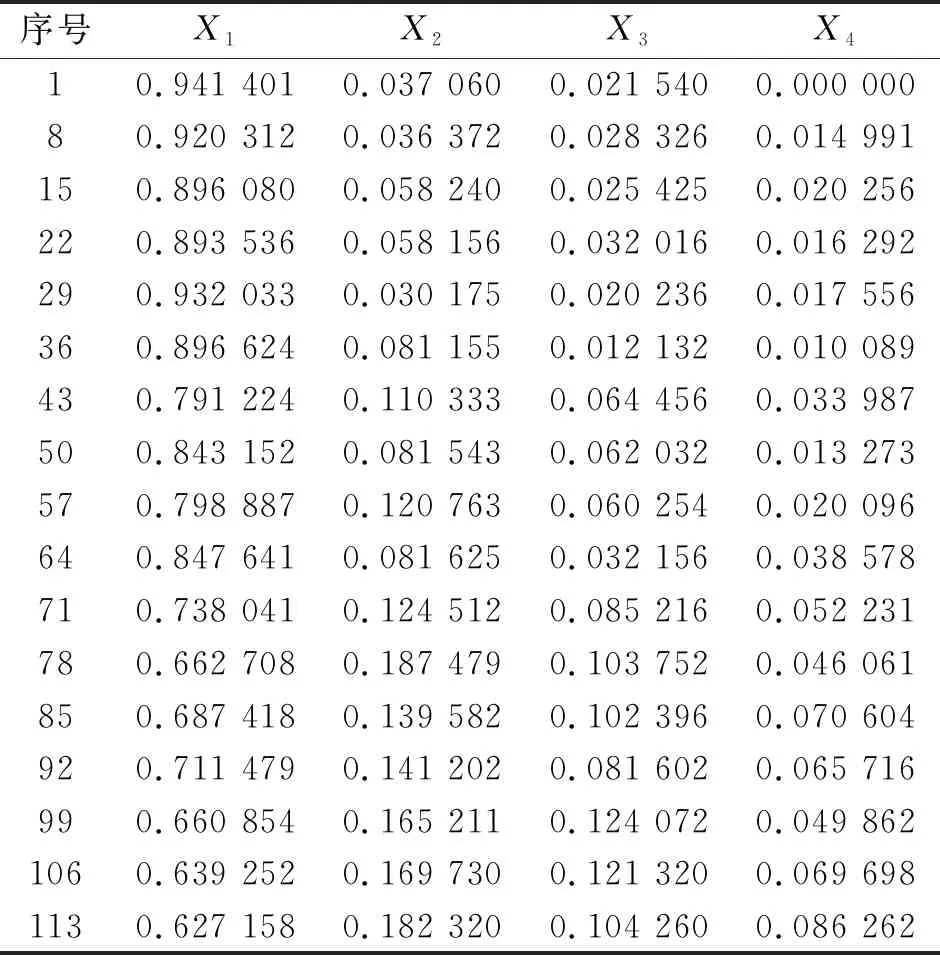
表3 样本数据角度状态概率分布表

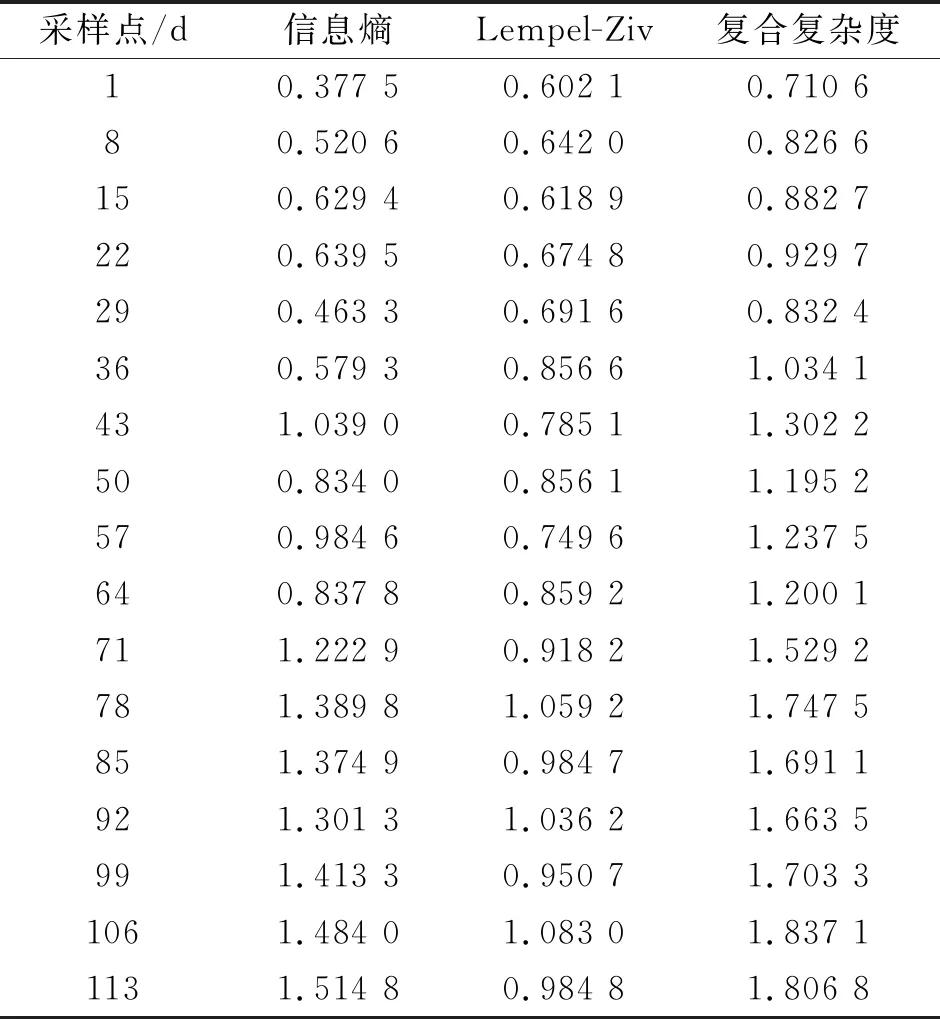
表4 设备角度性能复杂度计算结果

3 结果分析与讨论

3.1 扭矩指标结果分析

扭矩指标的信息熵值与标准化Lempel-Ziv复杂度熵值分别表征了设备性能的随机波动程度及状态无序程度，复合复杂度表征了拧紧机性能的整体水平，其具体变化趋势如图3所示。

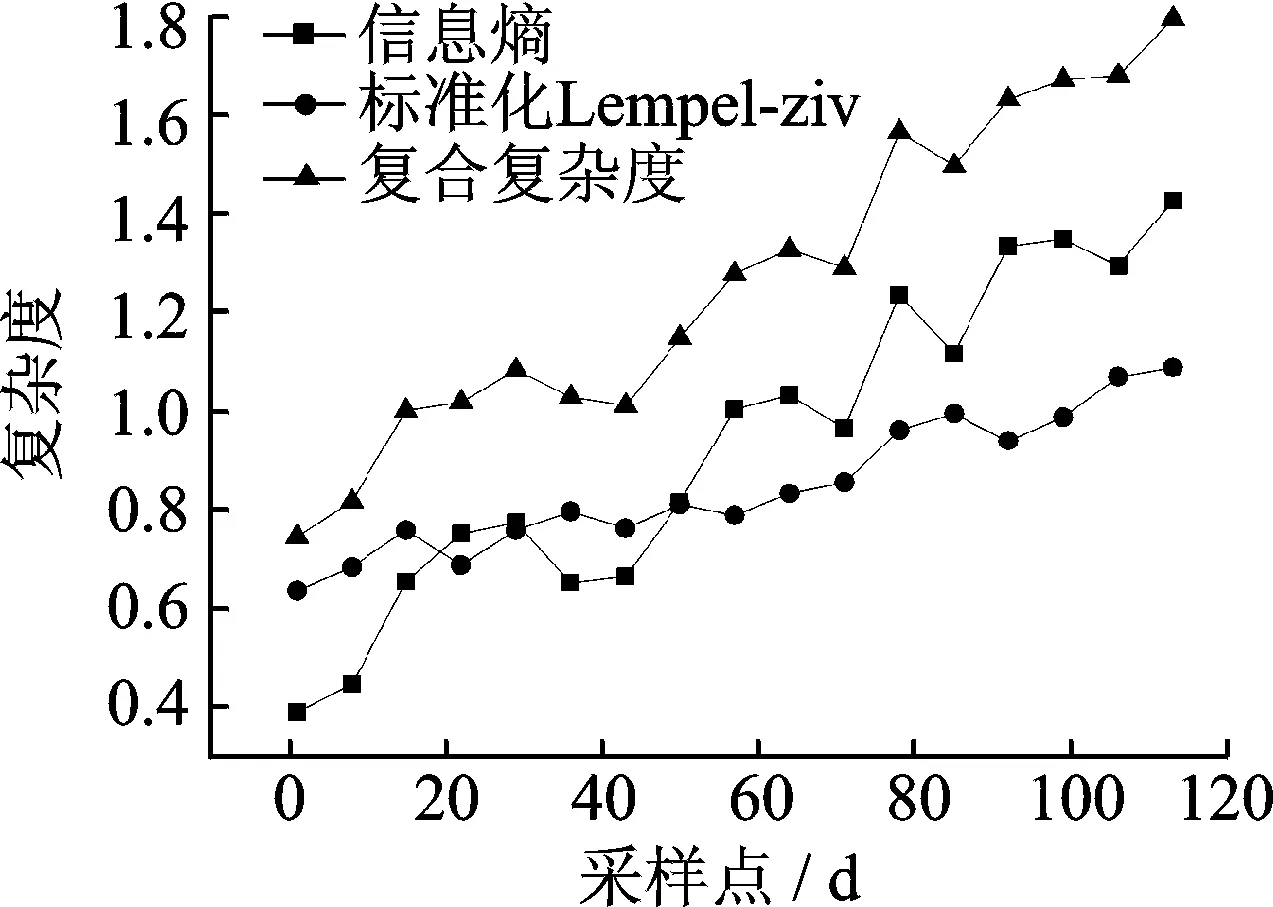
图3 扭矩数据的复杂度趋势Fig.3 Complexity tendency of torque data

两个维度的复杂度均反映出拧紧设备在长期运作后性能退化导致的复杂度上升，但任一个单一的复杂度值都不能综合地反馈性能的退化特点。例如在样本初期，信息熵值和Lempel-Ziv熵值都处于较低水平，说明设备性能的波动程度和性能状态的无序程度比较低，性能稳定性较高。在设备运行到第40 d左右，虽然Lempel-Ziv熵值没有明显的上升，但信息熵值却存在较高的增长，说明设备性能随机波动范围增大，而设备性能仍然处于一个相对稳定或稳定下降的阶段，不会出现突发故障现象。然而在样本后期，两个熵值都上升到较高水平，说明设备性能的随机波动程度和稳定性都退化到较低水平，需要及时进行维护。

3.2 角度指标结果分析

角度指标的信息熵值、标准化Lempel-Ziv熵值和复合复杂度值的变化趋势如图4所示。

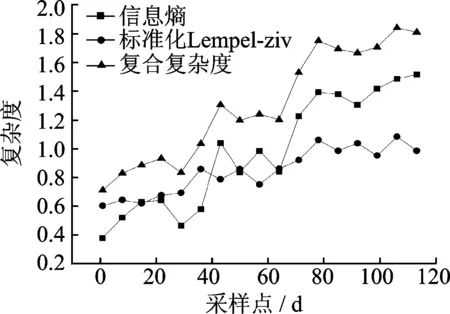
图4 角度数据的复杂度趋势Fig.4 Complexity tendency of angle data

信息熵值和Lempel-Ziv熵值均呈现随设备运行时间增加，出现性能退化和复杂度逐步升高的结果，在复杂性的两个维度上都与扭矩指标表现出相近的评估结果，验证了扭矩指标反映出的设备性能退化趋势。

3.3 复合复杂度对比分析

复合复杂度用以刻画拧紧设备性能的整体水平，将扭矩和角度的复合复杂度结果对比如图5所示。

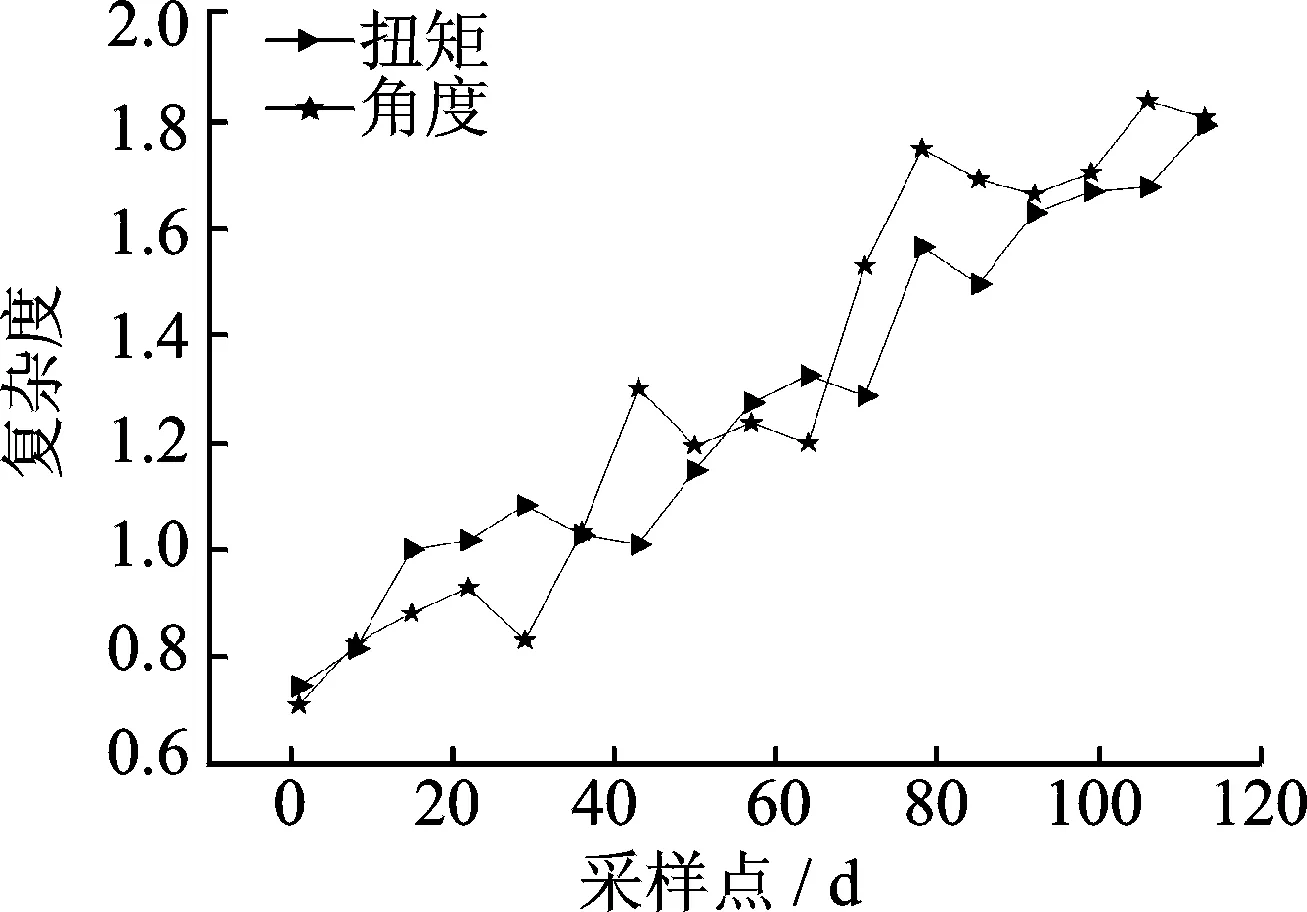
图5 复合复杂度对比Fig.5 Comparison of compound complexity

相同样本时间内的角度与扭矩数据都反映出一致的拧紧设备退化趋势，拧紧设备随使用过程性能逐渐退化，输出扭矩和角度指标随性能的退化而出现一定程度的波动和紊乱，交互验证了拧紧设备的性能退化水平。基于信息熵和Lempel-Ziv算法的拧紧设备性能评估方法是相得益彰的评估方法，能够从随机波动性和状态无序性两个维度反映拧紧设备的退化趋势，复合复杂度可以评估其整体性能水平。与以往通过设备的故障状况来反映设备性能相比，在正常运行状态下评估拧紧设备的性能水平更具实际意义。

4 结 论

1) 应用信息熵建立的拧紧性能复杂度模型，能够量化设备性能的随机波动程度；基于Lempel-Ziv算法的复杂性测度，衡量了设备状态的无序程度；复合复杂度能够综合评价设备的整体性能水平。比传统单一指标的评估方法更能准确反映拧紧设备的性能退化趋势。

2) 实例验证结果表明，扭矩和角度指标的评估结果均呈现一致的设备退化趋势。信息熵和Lempel-Ziv算法的测度结果具有一定的差异，从两个维度反映了设备性能状况。该方法建立在设备正常运行数据的基础之上，不同于以故障数据进行的评估，使其可以进一步为设备预知性维护提供定量参考。