基于方法集和DEA模型的黑龙江省灌溉用水效率评价

梁静溪，张安康，许耀文，李晨阳

(1.哈尔滨理工大学经济管理学院，黑龙江 哈尔滨 150000；2.东北农业大学水利与土木工程学院，黑龙江 哈尔滨 150000)

灌溉用水效率是评价灌区灌溉水利用情况的重要依据，是指真正被作物利用的水量与用于灌溉的水量之比。正确评价灌溉区的用水效率能够为节水灌溉发展提供科学合理根据[1-2]。对于灌溉用水效率的评价方法众多，如人工神经网络、主成分分析方法、SBM、DEA等。方琳等[3]运用非期望产出SBM模型，对31个省农业灌溉用水效率进行评价，分析了灌溉用水效率的差异性、变化趋势和发展潜力。张泽等[4]运用模糊评价法对灌溉用水效率进行测算。杨丹等[5]运用欧氏贴进度对农业灌溉用水效率进行排序。孙付华等[6]运用DEA-Malmquist指数对32个省农业用水效率进行测算[6]。综上可以看出，以往关于灌溉用水效率评价的研究都具有一定局限性，学者关于评价灌溉用水效率方法选择上存在单一性，无法避免单一方法自身的缺陷，进而增大计算误差。例如模糊评价法无法评价指标之间相关性、人工神经网络容易陷入局值、主成分分析解决非线性结果问题不理想、集对分析模型确定与否关系不清晰等。因此，为了提高计算准确性，缩小单一评价方法误差，本文运用由人工神经网络、主成分分析、模糊综合评价、集对分析构成的方法集模型对2016年黑龙江省20个大型灌区进行评价，且用DEA模型的评价结果作为参照，进一步突出方法集模型可行性，从而为科学评价灌溉用水效率提供一个新的思路。

1 研究区域概况

黑龙江省位于中国东北地区北部，占地47.3万km2，地势西北、东南高，东北、西南低，由山地、平原和水面构成，为温带季风气候，夏季雨热同期，冬季冰冷霜雪，具有四季分明的特点。黑龙江省也是我国重要粮食产区之一，主要盛产大豆、玉米、水稻。截止到2016年，黑龙江省共有水库1 156座，水库总容量2.75×1010km2，有效灌溉面积5 194万hm2，农业灌溉区317 830个，包括大(20 000 hm2以上)中(667～20 000 hm2)小(667 hm2以下)灌区，考虑到数据的可获得性，本文主要选取黑龙江省20个大型灌区进行灌溉用水效率评价。

2 评价指标选取

2.1 方法集模型的评价指标

灌溉水经过渠系输配水环节、田间用水环节，最后被作物所吸收利用，因此，渠系水和田间水综合影响灌溉用水效率[7-8]。基于数据获取的难易程度及评价指标选取的科学性、代表性原则，本文建立了图1所示的灌溉用水效率指标体系，其中，上面4个为渠系环节相关指标，下面4个为田间环节相关指标，各项评价指标的含义见表1[9-13]。

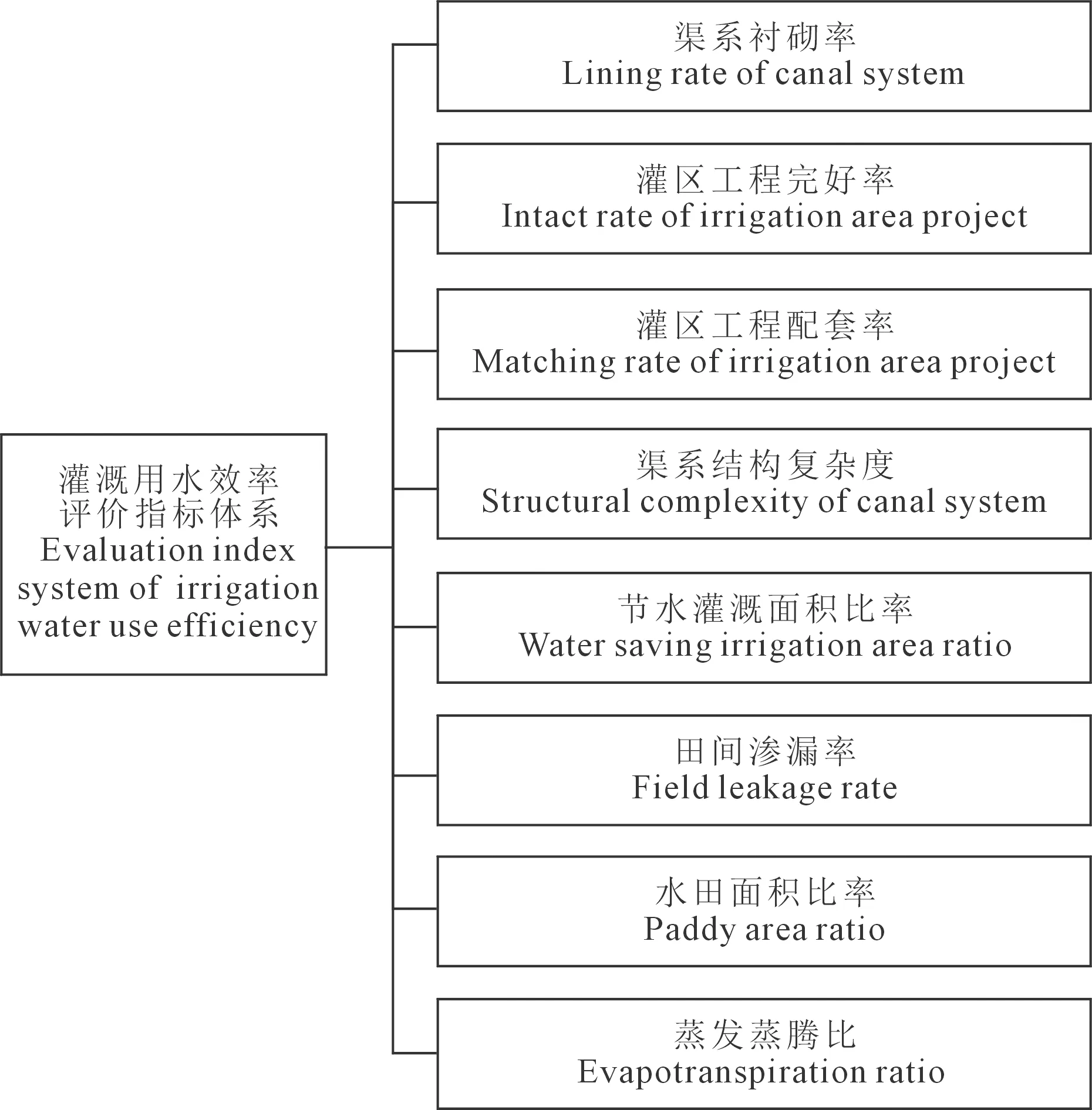
图1 灌溉用水效率评价指标体系图Fig.1 Evaluation indicator system of irrigation water use efficiency

表1 灌溉水利用率评价指标含义

2.2 DEA模型的评价指标

根据生产要素理论，本文选用农作物灌溉面积、农业机械总动力、农业劳动投入、农业灌溉用水量作为投入指标，农业总产值作为产出指标，如表2所示。且根据表3中变量之间的相关系数，反映出灌溉用水量与总产值之间具有很大的相关性，其相关系数为0.5428，说明水资源在农业生产中的重要性。

本文数据均来自《黑龙江省统计年鉴》(2017)、黑龙江省水资源公报(2017)。其中，农业灌溉用水量用农业用水总量的90%替代[14]，且本文数据经过归一化处理，保证了数据的平稳性。

3 研究方法

3.1 方法集模型

表2 农业灌溉用水效率评价指标

方法集模型是指在能单独完成对一个问题评价方法的基础上，根据相应的原则从中选择若干方法，并利用这些方法对所研究问题进行评价，进而通过合理的综合算法将它们进行优化组合。通过方法的集成，一方面可以弥补单一方法所带来的随机误差和系统偏差，另一方面，为解决一些问题提供了新思路[15-17]。针对黑龙江省农业灌溉用水现状，我们提出了基于方法集计算的灌溉用水效率模型，如图2所示，基于方法集模型的评价体系步骤如下：

第一：分别利用单一的评价方法对黑龙江省灌溉区的用水效率做出评价，得出每种评价方法的排序结果。

第二：运用Kendall方法对每一种评价方法进行一致性事前检验，如果结果具有一致性，则进入步骤四，如果结果没有一致性，则进入步骤三。

第三：如果结果没有一致性，我们则针对不同的方法进行两两一致性检验，将具有一致性的归类到一起，然后再对样本进行分析，选择出客观实际具有一致性的方法，返回步骤二。

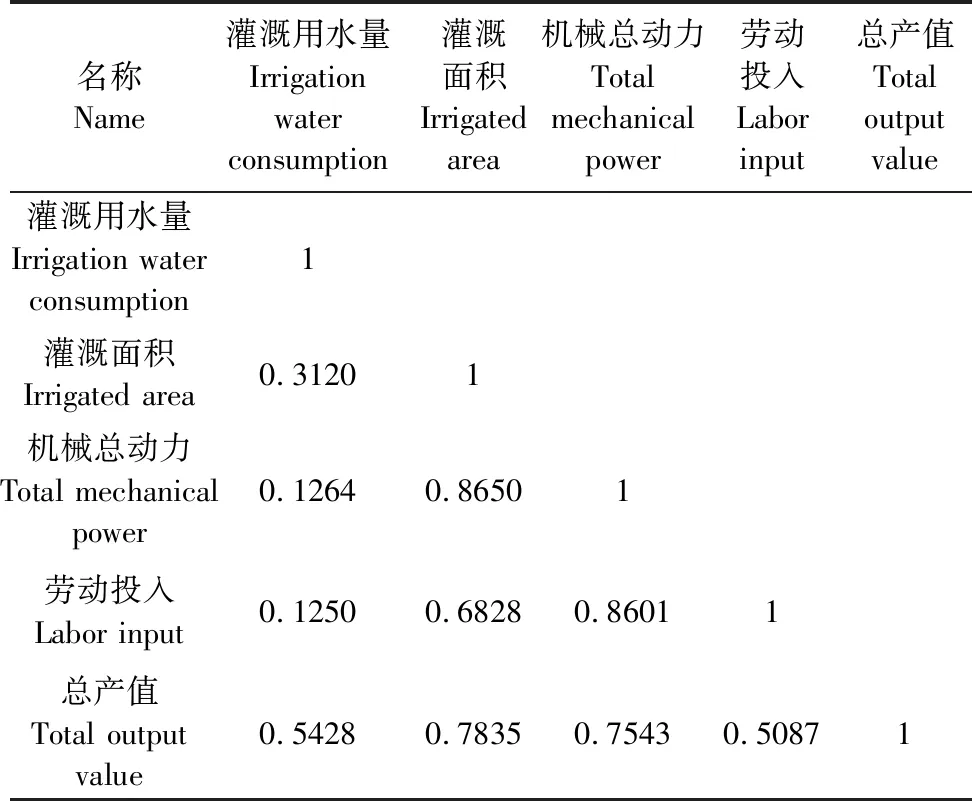
表3 变量间的相关系数

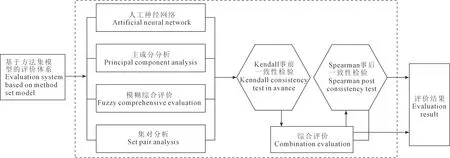
图2 基于方法集模型的评价体系Fig.2 Evaluation system based on method set model

第四：运用组合评价模型，即算数平均值法、Borda法和Copeland法对单一评价方法进行综合评价，进而得出结果并进行排序。

第五：运用Spearman方法进行事后检验，对组合排序结果和步骤二的结果进行检验，如果没有通过检验，对步骤三和步骤四进行循环。

3.1.1 单一评价方法简介 对于农业灌溉用水效率评价问题，在综合考虑各种方法和现状后，选取人工神经网络模型、主成分分析模型、模糊综合评价和集对分析模型作为一个方法集进行评价灌溉用水效率，下面对这4种方法进行简单介绍。

(1)人工神经网络模型：由于针对农业灌溉用水评价时会涉及到很多影响因素，并且他们之间都有一定的相关性，然而人工神经网络能够强有力解决这类问题。

(2)主成分分析模型：主成分分析模型的原理简单且操作方便。首先对数据进行标准化处理，计算变量之间的相关系数，形成矩阵。其次，计算相关系数矩阵的特征值和特征向量，一般认为贡献率在85%以上的为对应的主成分，进而计算主成分载荷量，最后根据特征向量和载荷量计算主成分得分。

(3)模糊综合评价模型：由于针对农业灌溉用水效率做出一个全面综合的评价，因此我们要建立一个全面的评价体系，并确定每个指标对应的权重，然而指标的权重都是来源于各个专家对于指标的主观判断，其具有模糊性，因此我们选取模糊综合评价模型进行构建方法集。

(4)集对分析模型：主要针对集对中两个集合确定与不确定性进行分析，由于农业灌溉用水效率评价中存在许多不确定性，因此我们选取集对分析模型构建方法集。

3.1.2 Kendall事前检验

(1)提出假设：H0：m种评价方法没有一致性；H1：m种评价方法有一致性。

(2)统计量X的构建：

X=m(n-1)W

(1)

(2)

(3)

其中，m表示评价方法的个数；n表示灌溉区的个数，yij表示第i个灌区在第j种方法下的排序数值。

3.1.3 组合评价方法简介 如果各个评价方法结果均通过事前检验，则运用算数平均值法、Borda模型和Copeland模型进行组合评价，得出评价结果[19-20]。

(1)算数平均值组合评价方法：该方法将单一评价方法的排序转换为分数Rik，即第1名得n分，第n名得1分，如果有一样的名次，则取它们的平均分，再计算不同得分均值，计算公式为：

(4)

其中，m表示评价方法的个数，k表示组合评价方法个数。如果出现平均值相等的情况，按照式(5)计算标准差，其越小排序的结果越靠前。

(5)

(2)Borda组合评价方法：此方法按照少数服从多数的准则，如果评价结果yi优于yj的数量比yj优于yi的数量多，可以表示为yi>yj，如果数量相等，表示为yi=yj。

Borda矩阵的定义B={bij}n×n

(6)

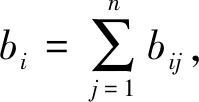
(3)Copeland组合评价方法：此方法能够充分考虑“次于”和“相等”的情形，弥补了Borda模型的不足之处，公式为：

(7)

(4)Spearman事后检验：运用Spearman法检验组合方法的评价与单一方法的评价结果之间的密切程度，从而选择最优的组合评价结果。计算过程如下：

构造统计量tk(k=1,2,3)

(8)

(9)

式中，n为灌区对象的数量；m为单一评价方法的数量；ρjk为第k种组合评价方法和j种评价方法的等级相关系数；xik、xij分别为第i个灌区在第j种评价方法的排序值和在第k种组合评价方法下的排序值。假设H0：第k种组合方法与原m种单一评价方法没有关系，H1：第k种组合方法与m种单一评价方法有关系；给定的显著性水平α下，查表对应临界值Cα，当tk>Cα时，拒绝原假设H0，接受H1，说明两种评价方法之间具有相关性[21]。

3.1.4 关联度分析 关联度分析是系统量化比较的一种方法，该方法能够分析系统内各因素间相互关系的密切程度，能够较好地解决样本容量小且线性关系不明显的相关性问题。关联的计算公式如下：

(10)

其中，n为灌区个数；r0i为灌溉用水效率与渠系水利用效率、田间水利用效率的关联度(i=1,2)；ξ为分辨系数，一般取值0.5；Δmin为各灌区灌溉用水效率与渠系水利用效率、田间水利用效率的最小绝对值差值；Δmax为各灌区灌溉用水效率与渠系水利用效率、田间水利用效率的最大绝对值差值；Δ0i(tk)为灌区灌溉用水效率与渠系水利用效率、田间水利用效率的绝对值差值。

3.2 DEA模型

数据包络分析方法(DEA)是经济学与运筹学知识相互交叉的一个方法，根据多投入和多产出的指标，运用线性规划进行相对效率评价的一种方法。该模型包含投入型和产出型两种，且根据规模报酬是否可变，分为纯技术效率(BCC)、规模效率和总技术效率(CCR)，本文主要运用投入型的总技术效率进行灌溉用水评价。

假设有n个决策单元，m个投入要素和s个产出要素，对于第p个决策单元，XP={X1p,X2p,X3p,…,Xmp}T为DMUi的投入要素，YP={Y1p,Y2p,Y3p,…,Ysp}T为DMUi的产出要素，则投入导向的CCR模型如下：

约束条件：

uk、vj≥0k=1,2，…，sj=1,2，…，m

(11)

其中，yki表示DMUi对第k种输出的产出量，xji表示DMUi对第j种输入的投入量，uk表示对k种输出的度量，vj表示对j种输入的度量。由于本文评价的是灌溉用水效率，只考虑水资源投入的灌溉用水量，因此构建分向量DEA模型，则上述分式方程式可以根据C2转换及对偶过程转变为如下模型：

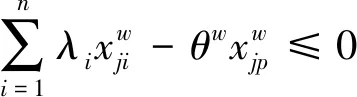
(12)

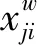
4 实例分析

本文以黑龙江省的样点灌区作为评价对象，选取兴北、朝阳、红旗岭、讷南、宋集屯、团山子、新城、新安、中和、河东、小河口、华炉、联丰、星火、双阳、富裕、永发、安邦河、龙头桥、石龙共计20个灌区，用方法集和DEA两种模型对灌区的灌溉用水效率进行评价。

4.1 方法集模型的结果

利用单一评价方法对黑龙江省20个灌溉区用水效率进行评价，如表5所示。

基于表5分别运用算数平均值法、Borda模型和Copeland模型进行组合评价，且经过2次迭代修正，得到结果如表6所示。

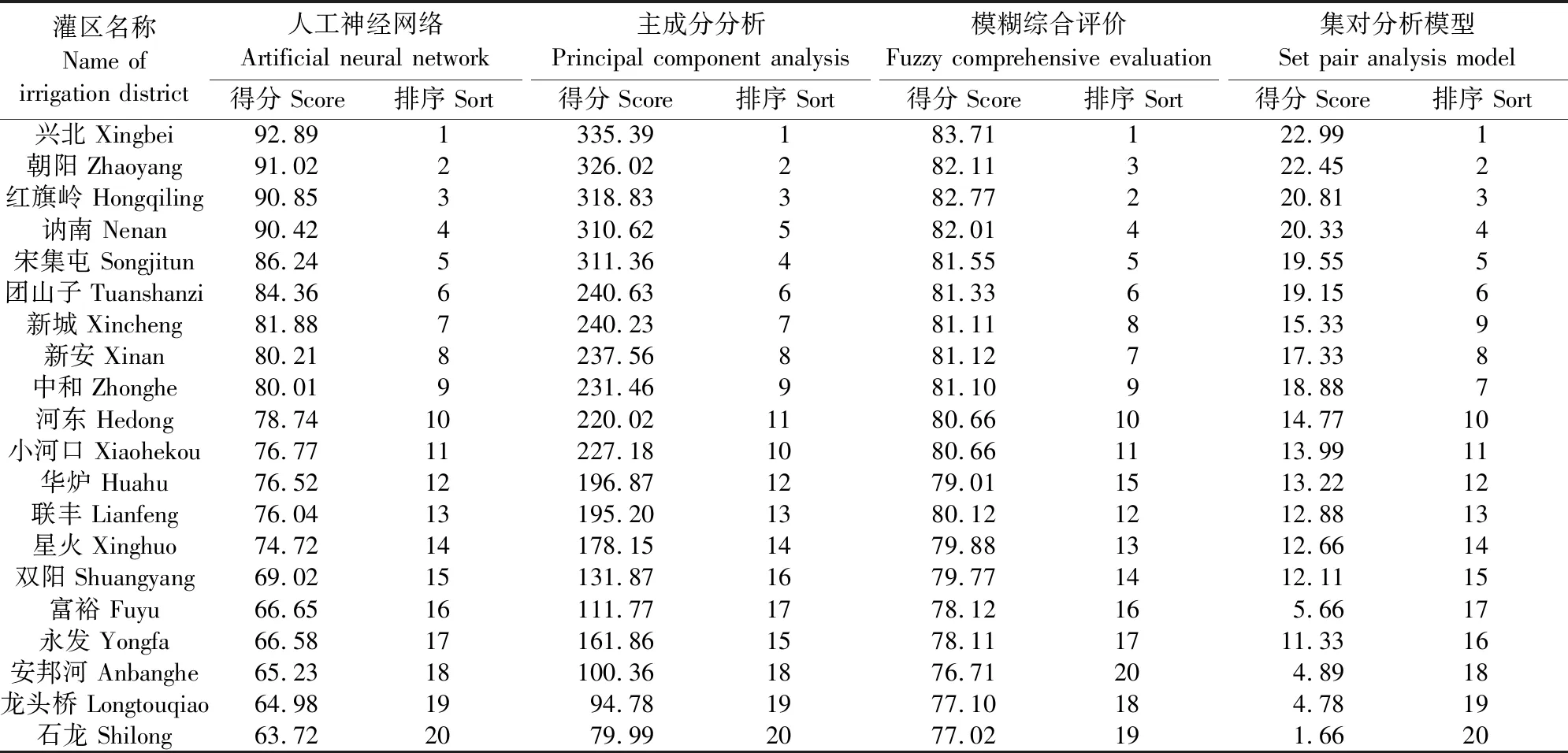
表5 各单一方法评价得分

表6 组合评价得分及排序

如表6所示，组合评价最终得出的排序结果一致，进而利用Spearman法对三种组合评价模型的结果与单一模型的结果进行事后检验，得出ta=33.59，tb=33.59，tc=33.59，经查表，在显著性水平α=0.01下，Cα=tα/2(18)=2.878，显然ta=tb=tc>tα/2(18)，表明组合评价方法与单一评价方法的排序结果有关，且证明方法集模型可以有效解决不同排序结果不一致的问题。

为进一步分析灌溉用水效率受不同灌溉环节的影响程度，同样利用方法集模型对渠系水利用效率及田间水利用效率进行排序分析，并灌溉用水效率排序结果与渠系水利用效率、田间水利用效率的关联度，结果见表7。

从表7可以得出，20个灌区灌溉用水效率与渠系效率平均关联度为1.779，与田间效率平均关联度为1.229，说明灌溉用水效率受渠系水效率大于田间水效率。其中，富裕灌区受渠系影响最大，关联度为3，兴北最小，为0.71；龙头桥受田间水效率影响最大，关联度为1.97，团山子受影响最小，为0.50。

表7 灌溉用水效率关联度排序

4.2 DEA模型的结果

基于公式和DEA-SOLVER软件，对2016年黑龙江省20个灌溉区进行了评价，如表8所示，发现灌溉区的效率值处于中等水平，其均值为0.78，还存在提升的空间，且排序结果与方法集模型的结果一致，值得一提的是，因为效率值有重复的，所以可能会存在一定的误差。

表8 DEA模型效率值及排序

通过DEA模型的结果参照可以看出，方法集模型不仅可以解决不同方法排序结果不一致问题，而且计算排序结果准确。从表6和表7也可以看出，兴北、朝阳、红旗岭和讷南四个灌区用水效率最高，富裕、永发、安邦河、龙头桥、石龙五个灌区效率值较低，排序靠后。用水效率受渠系水利用效率影响较大，田间水效率影响较小，可采取渠道衬砌，合理规划渠系布局等方式减少渠道输配水环节的灌溉水损失，采取控制灌溉技术及喷、滴灌溉等节水措施。

5 结 论

本文运用方法集对黑龙江省20个灌区的灌溉用水效率进行评价，并参照DEA模型，比较两种模型的最终结果，得出的主要结论如下：

(1)根据数据获取的难易程度与指标评价的科学性、代表性原则，建立了灌溉用水效率评价指标体系，其中，方法集模型主要从渠系输配水环节和田间用水环节两个方面进行综合考虑，DEA模型主要从土地、劳动力、技术、用水量四个生产要素进行综合考虑，两种模型虽指标选取不同，但都综合考虑了灌溉用水的特点，符合实际情况。

(2)利用方法集模型进行灌溉用水效率评价，弥补了单一评价方法存在的局限，并通过Kendall事前检验与Spearman事后检验，保证各方法与组合评价结果一致，从而验证了方法集模型的有效性，达到取长补短的效果，但对于方法集模型测算具体效率值方面还值得进一步研究。

(3)运用DEA模型有效验证了方法集模型的准确性，且该模型不指定任何生产函数，只通过投入产出值来建立线性生产前沿，应用方便灵活，为后人对灌溉用水效率评价提供了借鉴，但DEA方法只是将决策单元与其他最佳生产状态的决策单元进行比较，容易受个别极端样本的影响，且没有将运气、随机误差等因素与效率值分开，也会产生一定测量误差。

(4)黑龙江省灌溉用水效率的提高是一个不断探索改进的过程，这就需要了解目前灌溉用水效率现状，以此针对薄弱环节采取相应措施，富裕、永发、安邦河、龙头桥、石龙五个灌区效率值较低，排序靠后，受渠系水利用效率影响较大，田间水效率影响较小，可采取渠道衬砌，合理规划渠系布局等方式减少渠道输配水环节的灌溉水损失，采取控制灌溉技术及喷、滴灌溉等节水措施。本文虽然对灌溉用水效率关联度进行了分析，但对于影响黑龙江省灌溉用水效率因素还需深入研究，以此更有针对性地促进黑龙江省灌溉用水效率的提升。