基于改进兴趣度的船舶关联规则挖掘∗
2019-02-27刘建树李健维
刘建树 李健维 刘 霖
(中国人民解放军海军工程大学 武汉 430000)
1 引言
时空数据挖掘作为当前数据挖掘研究的前沿领域之一,备受学术界和工商界的关注。目标的时空数据能够反映对象的运动模式与规律,利用这些数据能够挖掘出目标实体的行为模式,并且可以根据这些模式来预测其下一步的行为,因此在各个领域中有着重要的应用[1~10]。
其中,AIS作为一种包含丰富的船舶航行信息的数据载体,集合了大量船舶的海上交通信息。通过对这些海量信息进行挖掘,能够获取其中蕴藏着的海上交通特征,发现船舶之间行为的内在关联性或者船舶本身活动的规律性。将这些行为模式作为发掘出的知识整合规约并存储,就能够形成重点船舶的行动模式数据库。为此,本文选用部分南海海域的船舶AIS数据,采用算法对船舶之间的关联规则进行挖掘,试图提取出它们之中具有时空关联关系的船舶集群。
2 关联规则挖掘
关联规则挖掘主要研究空间对象随时间发生变化的规律,即在传统关联分析的基础上加上了时间和空间约束,以发现时空数据中处于一定时间间隔和空间位置的关联规则。发现这些关联模式具有重要的应用价值,如发现购物中商品之间的关联性、群体性行动的团体成员之间的联系性等。
关于时空关联规则的挖掘更注重实体之间的时空关系,维度的增加也导致其研究方法相对普通的关联规则挖掘来说更为复杂多用。Tao等[11]提出一种基于时空索引和简图技术的方法来加快搜索数据的速度,以获得准确度更高的关联规则;Verhein等从区域面积以及时间间两个角度出发,引入了目标在时域上跨区移动的时空关联规则挖掘方法 STAR-Miner[12~13],此后,又进一步引入了序列时空关联模式在这一领域进行了更为深入的研究[14~16];Lee等[17]提出一种可以挖掘多层次粒度的时空关联规则的算法;Gidfalvi等[18]引入一类旋转方法将挖掘工作划归为为传统购物篮问题实现了时空关联规则挖掘;Yang等[19]在解决蛋白质折叠轨迹的过程中提出了两种时空关联框架;Leong等[20]则提出一种能够探测多种动态模式的关联规则挖掘方法。
3 面向船舶海洋时空数据的关联规则挖掘算法
3.1 事务集生成
3.1.1 基于时空块的数据分割
为了使用Apriori算法对船舶数据进行挖掘,首先要利用原始AIS数据形成可供算法处理的事务集。本文采用一种划分时空块的方式来实现这一功能。
将整个数据集按照经度0.02°、纬度0.02°、时间间隔1200s的分度值进行划分,可以得到若干个数据块。选取如上分度值的理由如下:在赤道上经度差1°对应的实际距离是111km,在经线上纬度差1°对应的实际距离约是111km,在除赤道外的其他纬线上,经度差1°对应的实际距离是111*cos(纬度)。假设船舶的平均速度为15海里每小时,则同一时空块内的两船背向航行时,两船的最远距离约为13*0.33*1.8*2+111*0.02=17.6km,约为目视距离极限。考虑到地球曲率问题和不同的海洋情况,取此分度值较为合适。
每一数据块内的AIS数据所代表的船舶号归为同一个事务中,即形成初始事务,相同时空块内出现的船之间具有可能具有某种关联关系。
3.1.2 事务中的相同船舶去重
在一个时空块中,会存在某条船有多条数据的情况。利用实测数据得到的结果中也能够发现这种情况较为普遍,由于不同船舶之间的关联关系是求解问题的重点,因此在之后的处理中只需要知道同一事务内不同的船舶编号即可,因此对于同一时空块内相同的船舶编号予以删除。
3.1.3 生成事务集布尔矩阵
定义事务集布尔矩阵如下:设经过Step2得到的成没有重复船舶编号的事务共有N条,所包含的船舶共有M个。则生成一个N×M的布尔矩阵,矩阵的每行表示一个事务,矩阵的列编号 j对应船舶编号 j。若第i条事务包含船舶 j,则事务集的布尔矩阵 C中的元素 C(i,j)=1,反之C(i,j)=0 。
3.2 基于改进兴趣度的关联模式挖掘
3.2.1 基于支持度和置信度的关联规则挖掘
一般来说,传统的判定某个推理是否是关联规则的指标有两个,分别为支持度和置信度。
支持度(Support)表示同时包含A和B的事务占所有事务的比例。如果用P(A)表示使用A事务的比例,那么Support=P(A&B)。
置信度(Confidence)表示使用包含A的事务中同时包含B事务的比例,即同时包含A和B的事务占包含A事务的比例,那么Confidence=P(A&B)/P(A)。
传统方法设置了两个阈值,分别为最小支持度阈值min-sup和最小置信度阈值min-conf。若某个推理A->B满足:

则判定A->B是一条强关联规则。
但是,实际上仅仅通过上述两个指标判断得出的关联规则会出现两个问题,下面举例说明。其一,当假设某个事务集中发生了下列项集的出现情况。

表1 例事物集
按照上边的计算方法可以计算出二者置信度 :Confidence(¬A→¬B)=0.66,Confidence(A→¬B)=0.75。这两条推理的支持度和置信度都分别满足支持度阈值和置信度阈值的限制,因此都会被判定为关联规则。但实际上这两条规则显然是互相矛盾的。
其二,当将A、B、¬A 、¬B当作四个不相关的独立事务时,B事务发生的概率为0.3,而A事务发生并且B事务发生的概率为0.25,也就是说如果设置了A事务发生这个条件,那么B事务出现的比例反而降低了。这就说明A事务的发生和B事务的发生是排斥的。
可见,仅仅利用支持度和置信度很容易挖掘出实际上并不相关的“虚假的”关联规则,这显然是十分致命的问题。为此,就需要引入新的度量标准来解决这一问题。
3.2.2 基于提升度的关联规则挖掘
为了解决上述两项问题,引入一种被广泛使用的称为提升度的概念。
提升度(Lift):表示“包含A的事务中同时包含B事务的比例”与“包含B事务的比例”的比值。公式表 达 :Lift=(P(A&B)/P(A))/P(B)=P(A&B)/P(A)/P(B)。
提升度反映了关联规则中的A与B的相关性,提升度>1且越高表明正相关性越高,提升度<1且越低表明负相关性越高,提升度=1表明表示X与Y相互独立,没有相关性。
利用此定义再次省视上一节提到的问题,可以发现:Lift(¬A→¬B)=0.95,Lift(A→¬B)=1.07。显然,此时由于A→¬B的提升度大于1,A和¬B具有正相关关系,因此A→¬B被选择为关联规则为,¬A→¬B则被删去,从而消除了规则之间互相矛盾的问题。
但是,在本文所解决的问题中,由于AIS数据库生成的事务较多,因此计算求得的Lift都普遍较大。虽然从定义上讲,这些关联规则的Lift可能都大于1,因此关联规则的前后项都具有正相关关系,但是如果想要进一步提高Lift的阈值标准来寻找更可信的关联规则时,阈值设定就成为了困难。为此,需要进一步寻找更实用的评价指标对关联规则的相关性进行评判。
3.2.3 基于改进兴趣度的关联规则挖掘
为了解决3.2.2中提出的问题,引入了一种称为改进兴趣度(Interest)的概念[21]。其表达式为

改进兴趣度(Inerest)将Lift映射为一个有界的数值,从而能够给定阈值实现更有效的规则筛选,此外,Lift越大其对应的改进兴趣度越大,因此利用改进兴趣度判定规则的相关性称为可能。
下文中即使用改进兴趣度来衡量关联规则的可信程度。换言之,本文判定A→B为关联规则的判据如下:

3.3 算法求解流程
选用Apriori算法作为基础算法对AIS数据进行挖掘处理。
3.3.1 相关定义
定义1:事务
事务由若干个项目组成,在此问题中项目表示船舶的编号。形如Ij={X1,X2,X3,…},Ij表示第j个事务。
定义2:事务集
事务集由全体事务组成D={I1,I2,…,Ij,…,In},Ij表示第j个事务。
定义3:支持度
事务集D中包含项集X的事务个数,称之为项集X的支持数,用count(X)表示。而项集X的支持度用sup(X)表示,公式如下:
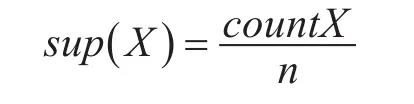
其中,n表示事务集D中事务的总数。
定义4:置信度
包含项集X1的事务中同时包含项集X2的事务的比例,即同时包含项集X1和项集X2的事务占包含项集X1的事务的比例,用con(X1→X2)表示,公式如下:
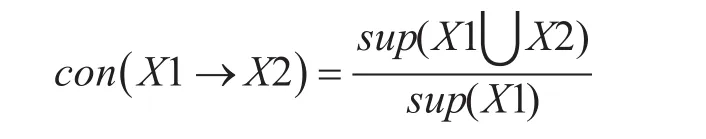
3.3.2 算法步骤
具体算法步骤如下。
Step1:数据预处理,生成事务集
详细处理过程见文章4.3.2。最后得到01矩阵,即附件中的SW矩阵。初始化迭代值K=0。
Step2:生成候选项集
对于候选1项集,根据不同船舶号数量直接生成单位矩阵作为其候选项集。
对于候选1+K(K>0)项集的生成,算法采用对表示不同事务的K项频繁集矩阵的行向量两两进行或运算,再进行筛选,留下只有1+K项的事务行,组成新的候选项集。
Step3:生成频繁项集
Matlab中使用find函数找出候选K项集的每一个事务行向量值为1的列数,取出SW矩阵中对应列向量,对其每一行进行筛选和计数,其行向量值全为1时计数1次,得到count(X1∪X2∪…)。
然后分别根据两种情况筛选出符合条件的频繁1+K项集。一是根据最小支持数min_count=9(本实验采用的最小支持数为9),从中筛选出符合条件的频繁1+K项集,及支持数大于等于9时,取其值生成频繁项集。
Step4:迭代
如果新生成的频繁项集不为空,令K变为K+1,转到Step2,否则转到Step5。
Step5:生成关联规则
根据最小置信度和最小改进兴趣度判定每个推理是否是强关联规则。
对于包含全部频繁项集的矩阵Z,取其行向量两两相比较,若两矩阵的数值和不相等,则对其两行向量进行异或运算,再对得到的行向量做求和运算,若其值小于原两个行向量的其中某一行向量数值求和值,则能推出相应的关联规则。
求出所有关联规则后,输出结果,算法结束。
4 检测结论
4.1 实验环境
程序运算平台为联想ZX50笔记本电脑;操作系统为 Window10;CPU 为 core i7-4720;内存为16GB;程序处理软件为Matlab R2014B。
4.2 数据准备
选取一份船舶AIS记录,提取每条记录的经度、纬度、时间戳和船舶号数据,存入excel中,作为挖掘用的源数据。选用的数据中共包含393条船,70万条AIS记录,经度跨度为东经109.94°~110.2°,纬度跨度为北纬20.11351°~20.193665°,时间跨度为2675816s。
4.3 实验结论
4.3.1 基于支持度和置信度的关联规则挖掘结果
设置最小支持度为9,最小置信度为0.6,利用上面的数据进行关联规则挖掘,共得到11条关联规则,结果如下:

表2 基于支持数置信度的关联规则挖掘结果
观察表2可以发现,表2中1~3行的关联规则是三条船舶之间的关联规则,它们之间两两都能推出第三条船;4~6行及7~9行也是相同的情况。
4.3.2 基于动态阈值和改进兴趣度的关联规则挖掘结果
设置最小支持度为动态阈值V,最小改进兴趣度为0.99,利用上面的数据进行关联规则挖掘,共得到6条关联规则,结果如下:观察表2可以发现,原本表1中第7行之后的关联规则被删去,只保留了前6条关联规则。

表3 基于改进兴趣度的关联规则挖掘结果
算法比较结果显示,相对于使用传统的基于支持度和置信度的算法而言,基于改进改进兴趣度的关联规则得出的结果数量更少,船舶的关联性更紧密,可见算法的有效性。
4.3.3 可视化分析
选择算法中挖掘得到的改进兴趣度最大的关联规则包含的船舶,做出其航迹,如下图所示。
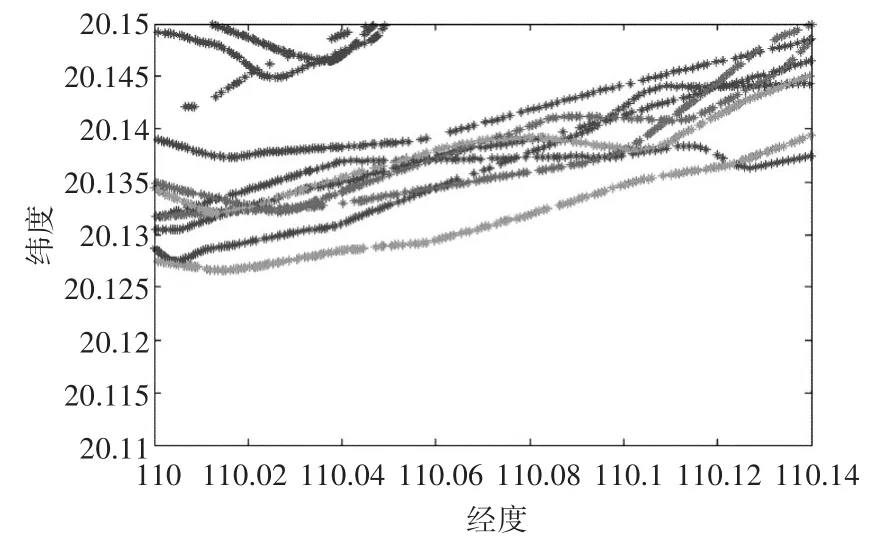
图1 关联规则中的船舶航迹
其中,横坐标为东经,纵坐标为北纬,上图中不同颜色的点表示不同的船舶。可以看到挖掘出的三条船舶的航迹相似度很高,可见该算法的有效性和实用性。
5 结语
本文以改进的Apriori算法为基础,对AIS数据进行预处理后生成的事务集进行挖掘分析以求取船舶之间的关联规则。首先将AIS记录提取后分块,并将结果转换成了能够更快运算的01矩阵模式;然后,在Apriori算法运行过程中,引入了改进兴趣度指标,消除了可能存在的误判问题,使最终的关联规则结果更加准确,可信度更高。
