GB 4706.23-2007标准中防火保护罩面积的计算方法及案例分析

郭记伟 张 豪 申丹伟

（重庆仕益产品质量检测有限责任公司 重庆 400013）

引言

防火保护罩是可见发光的辐射式加热器的部分外壳，通过它可以看到发热元件并且防止直接接触发热元件或带电部件[1]。同时防火保护罩开口面积不合理，将影响产品的整体强度、温升，引起烫伤、触电、火灾的危险[2]，对产品的使用者造成生命威胁。标准对防火保护罩开口面积有明确的指标规定，在GB 4706.23-2007《家用和类似用途电器的安全第2部分：室内加热器的特殊要求》标准中要求防火保护罩开口面积与防火保护罩总面积的比值k不少于50 %，k计算如下。

根据比值k大小，确定防火保护罩是否合格，其中难点是如何求得防火保护罩的总面积和总开口面积。

本文结合产品的检测实例来介绍有关防火保护罩总面积、总开口面积的计算案例分析。

1 防火保护罩判定目前存在的问题

防火保护罩类型较多，目前没有针对性的给出面积计算公式，无法有效的求得防火保护罩总面积、总开口面积，进而得不到比值k具体值，影响防火保护罩合格与否的判定，进而影响整体产品的安全性的符合性判定。对防火保护罩面积比值k合格与否的判定，多数凭经验取值、粗略计算得出，这种方式既不科学且不符合标准要求，特别对于比值k处于50 %左右时，会出现错判和误判。基于这些原因，必须要求得防火保护罩总面积、总开口面积及比值k。常见的几种防火保护罩实例如图1～ 图7。

2 防火保护罩面积计算案例整体分析

对防火保护罩结构图形简单且有规律的，则直接测量相关数据求得面积；对图形复杂的，直接求面积比较困难，则把防火保护罩图形分解成若个区域，分析每个区域图形的特征，求得相应区域图形的面积，通过计算求得防火保护罩总面积、总开口面积。

复杂图形的防火保护罩，求解面积案例中涉及到微积分、曲线拟合方法相关知识，因此，需有引入微积分、曲线拟合方法的相关知识。

1）曲线拟合方法求方程

曲线拟合方法是由给定的离散数据点，建立数据关系(数学模型)，求出一系列微小的直线段把这些插值点连接成曲线，只要插值点的间隔选择得当，就可以形成一条光滑的曲线，从而得到曲线的方程[3]。

2）上半平面内曲线绕x轴旋转而成的旋转曲面面积

上半平面内曲线L:y=f(x)(a≤x≤b)绕x轴旋转而成的旋转曲面面积公式[4]为：

因此，在曲线形状确定的情况下，在曲线上取一定数量的离散数据点，通过数据分析软件，得到曲线方程，再根据公式（2）得到曲线绕x轴旋转而成的旋转曲面面积，也即是防火保护罩的面积。

图1 防火保护罩实例1

图2 防火保护罩实例2

图3 防火保护罩实例3

图4 防火保护罩实例4

图5 防火保护罩实例5

图6 防火保护罩实例6

图7 防火保护罩实例7

3 防火保护罩面积计算案例分析

根据上述分析，对常见的几种防火保护罩实例，如图1～图7所示，进行详细的总面积、总开口面积计算案例分析。

3.1 实例1面积计算案例分析

实例1防火保护罩图形简单、有规律，整体为矩形形状，孔眼形状均相同为圆形。因此，测量孔眼直径，求得单个孔眼面积S11；当孔眼数量为m1时，求得防火保护罩的总开口面积S12=m1S11；测量防火保护罩边长，求得防火保护罩总面积S13。

3.2 实例2面积计算案例分析

实例2防火保护罩，整体形状为矩形，有两种规格的孔眼，形状都为矩形。因此，测量两种规格的孔眼边长，求得相应规格的孔眼面积分别为S21、S22；当两种规格的孔眼数量分别为m2、m3时，求得防火保护罩的总开口面积为S23=m2S21＋m3S22；测量防火保护罩边长，求得防火保护罩总面积S24。

3.3 实例3面积计算案例分析

实例3防火保护罩图形复杂，分析图形可知：

1）径向铁丝形状、直径都相同，圆环铁丝直径互不相同；

2）此图形总面积等效于曲线L11绕此图形中轴线旋转一周所形成图形的面积；

3）径向铁丝与圆环在交叉区域内成垂直状态；

4）任意一条径向铁丝与每条圆环的交叉区域在整个图形上所占的面积为径向铁丝直径与圆环铁丝直径的乘积；

5）任意一条径向铁丝在整个图形上所占的面积为径向铁丝直径与其长度的乘积；

6）每个圆环在整个图形上所占的面积为圆环周长与其铁丝直径的乘积。

测量曲线L11上的两段长度H1、H2，径向铁丝直径R，圆环的直径分别为d1、d2、d3，相应圆环的铁丝直径分别为r1、r2、r3。根据曲线拟合方法，求得曲线L11方程；曲线L11上H1段绕图形中轴线旋转一周所形成图形的面积为S32。

根据公式（2），求得防火保护罩总面积S31、S32。

当径向铁丝条数为m4时，求得防火保护罩的总开口面积为：

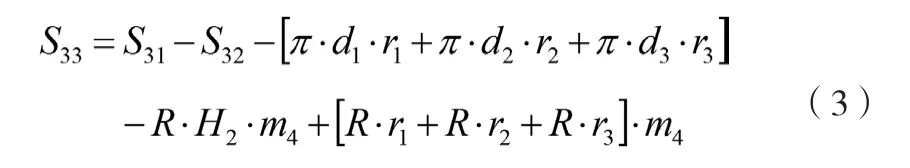
3.4 实例4面积计算案例分析

实例4防火保护罩，孔眼形状均相同，难点是如何求得一个孔眼的面积；进一步分析可知，孔眼图形为中心对称图形，沿着对称中心平分孔眼，得到规格1、规格2两个形状、面积都相同的孔眼，建立规格1孔眼图形的平面直角坐标系，如图8所示。根据曲线拟合方法求得曲线L21、L22、L23方程，分别为：

图8中，三条曲线与Y轴围成的面积为：

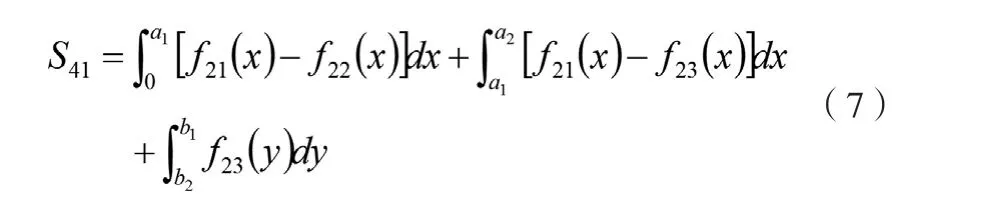
图4中，孔眼的面积（即2倍的S41）为：

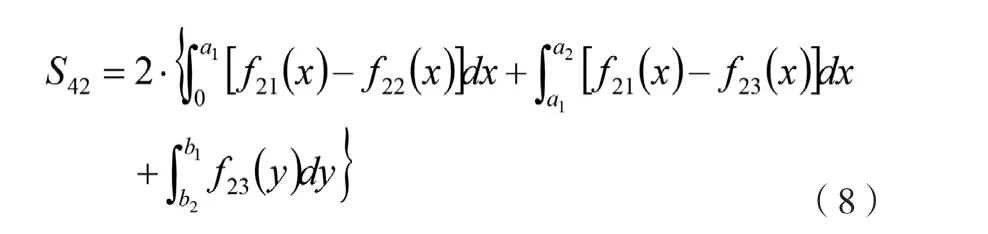
当孔眼的数量为m5时，求得防火保护罩的总开口面积为：

图8 规格1孔眼图形的平面直角坐标系

测量防火保护罩边长，求得防火保护罩总面积S44。

3.5 实例5面积计算案例分析

实例5防火保护罩，孔眼有两种规格，规格1的形状为圆形，测量直径，求得其面积为S51；规格2的形状为不规则的四边形，数量为m6；建立规格2孔眼图形的平面直角坐标系，如图9所示，根据曲线拟合方法求得曲线L31、L32、L33、L34方程，此4条曲线围成的面积即为图5中规格2孔眼的面积，把四条曲线围成的区域分解成3个区域，参考公式（7）方法，求得3个区域的面积分别为S52、S53、S54，求得规格2孔眼的面积为S55=S52+S53+S54。

求得防火保护罩的总开口面积：S56=S51+m6·S55。

根据曲线拟合方法和公式（1），求得防火保护罩的总面积S57。

3.6 实例6面积计算案例分析

实例6防火保护罩，实则为实例2、实例4防火保护罩的组合，根据实例2、实例4防火保护罩面积计算案例分析，采用相同求解方法、相加，求得实例6防火保护罩的总面积和总开口面积。

3.7 实例7面积计算案例分析

实例7防火保护罩，是实例3、实例5防火保护罩图形的组合，通过分解图形、分区域求面积，求得实例7防火保护罩的总面积和总开口面积。

图9 规格2孔眼图形的平面直角坐标系

综上，根据面积计算案例分析，求得实例1～实例7防火保护罩的总面积和总开口面积，根据公式（1），计算得到比值k ，判定出实例1～实例7防火保护罩是否合格。

4 结语

本文分析了防火保护罩开口面积和总面积在判定案例中存在的难点及问题；结合市场上常见防火保护罩对防火保护罩的面积计算进行了整体分析，并根据不同结构图形，对每个实例进行了详细的总面积、总开口面积计算案例分析，对于一线的检测工作有一定的借鉴和指导意义。