大规模MIMO系统中低复杂度的码本搜索方法

刘剑飞，何利平，陶颖，刘迪，曾祥烨，王蒙军

（河北工业大学电子信息工程学院，天津 300401）

1 引言

近年来，随着物联网的盛行和移动物联网设备使用量的快速增长，人们对无线数据流量的需求急剧增加。新一代无线通信（5G）技术受到越来越多研究者的关注[1-2]。同时，中、美、日、韩、欧等为代表的多个国家和地区开展了广泛实践和验证，加快了5G的商用化进程[3]。作为5G关键技术之一的大规模 MIMO（multiple-input multiple-output）无线传输技术通过在基站配备大量天线将有可能使频谱效率和功率效率在 4G的基础上再提升一个量级[4]，并利用多天线技术，在空间划分中可以更精确地控制无线电波的传播方向[5]。

目前，研究者对大规模MIMO的研究主要包括信道模型[6]、信道信息获取[7]、天线设计[8]等方面。其中在下行用户预编码传输中使用的预编码技术受到很多研究者的关注。根据预编码矩阵是生成在基站端还是用户端，预编码技术分为基于非码本的预编码和基于码本的预编码。非码本预编码是以时分双工（TDD，time division duplexing）系统中的上下行信道互异性获取的完整信道信息为前提[9]。然而大量的天线单元使得传统的上下行互异性校验方法很难直接使用，信道信息的获取成为限制大规模MIMO的瓶颈问题。这样，基于码本的预编码成为大规模MIMO预编码技术的重要选择。针对传统MIMO系统已经有很多很成熟的码本设计。如矢量量化码本[10]、离散傅里叶变换（DFT，discrete Fourier transform）码本[11]、Kerdock码本[12]、Grassmannian码本[13]以及 Householder码本[14]。对于强相关信道来说，DFT码本是一个很好的选择[15]。但是DFT码本的数量有限，即在满秩时可用的预编码矩阵是唯一的，对信道的匹配不够准确。而旋转DFT码本通过增加旋转因子改进了DFT码本量化精度不足的缺点[16-18]，被认为是大规模MIMO系统中一种极具应用前景的码本。由于大规模MIMO基站端天线阵列的间距较小，水平维度和垂直维度信道都具有强的相关性，所以水平维度和垂直维度都可以使用旋转DFT码本。然而，虽然码本数量越多越能更好地匹配信道性能，但码本数量的增加导致最优码字的搜索复杂度也随之增加，搜索最优码字的时间变长[19]。这种搜索复杂度的升高加大了对用户终端的设计要求，限制了基于码本的预编码技术的实现。因此，降低码字搜索的复杂度对码本的应用具有重要的意义。在传统的MIMO系统的码本搜索的研究方面，Zhang等[20]利用距离的三角形不等式原理，提出了一种约束条件来避免计算非最优码字与输入矢量的弦距离；Lin等[21-22]基于FFT分组提出了一种预编码选取准则，减少了矩阵转置和矩阵乘法的运算；Kim等[23]提出一种闭环下行链路波束形成方案，其中码本中的波束成型矢量根据弦距离被划分为一定数量的组；吕磊等[24]根据子空间距离与弦距的等效性提出了一种基于子空间距离的搜索方法，简化了每一次搜索的运算量。在面向5G的大规模 MIMO系统码本搜索方法的研究中，Ahmed等[25]提出一种基于行列式的搜索方法，即利用在相关大规模 MIMO信道中统计预编码的最优性；在其进一步的研究中又提出一种分层的码本搜索算法[26]。这2种方法均是针对正则化迫零预编码设计的码本搜索方法，通过将搜索过程聚焦到较小的码字集合实现复杂度的降低，但是误码率性能会随着信噪比的升高而与传统搜索方法的差距变大。

本文针对 5G大规模 MIMO系统中基于旋转DFT码本的预编码技术，提出一种低复杂度的码本搜索方法。该方法基于一种码本分组的方法，并根据旋转DFT码本矩阵中相同列的弦距离最小，且弦距离越小的预编码矢量越相似，即与信道的匹配程度越好的特性，通过减少搜索次数降低搜索复杂度。该方法对基于码本的5G预编码技术具有参考价值。

2 系统模型

本文使用的大规模 MIMO单用户下行信道预编码系统如图1所示。

图1 大规模MIMO下行信道预编码系统架构

基站端配置均匀平板天线阵列，有Nt=Nth×Ntv根发射天线，水平维度和垂直维度天线数分别为Nth和Ntv，用户配置Nr根接收天线。基站端输入的码字流q经过调制后生成复调制符号d（i），然后进行层映射，即把调制后的符号映射到层x（i）上传输，再进行预编码操作，即把层映射之后的复调制符号映射到相应的虚拟天线端口的资源上的向量块y（i）上；其中q为未经过信道编码的伪随机序列，x（i）表示层映射之后的数据，y（i）表示预编码之后的数据。之后发送信号经过winner 2信道，加高斯白噪声之后被接收端接收，然后进行信道估计，这里假设信道估计矩阵为如式（1）所示。

将3D信道模型分为水平维度和垂直维度可以得到第i（i=1,2,…,Nh）水平维度和第j（j=1,2,…,Nv）垂直维度的子信道为[27]

在用户端，用户对传输信道进行信道估计，依据信道估计结果和码本搜索方法在码本集合中选取各自的预编码向量，并将已选的预编码向量的索引发送给基站端。用户接收到的信号可以表示为

3 码本搜索方法

码字搜索是预编码技术中用户端的关键问题，高的搜索复杂度会提升对用户终端的设计要求。因此简化码字的搜索复杂度对于用户端和整个系统来说都是十分必要的。

3.1 码本生成

大规模MIMO基站端配置间距较小的天线阵列，水平维度和垂直维度信道都具有强的相关性，因此旋转 DFT码本更加适合具有强相关性的 3D MIMO信道。本文设水平维度和垂直维度天线数相同（Nh=Nv），系统水平维度和垂直维度使用同一个码本集合。根据旋转DFT码本的生成式得到所需的旋转DFT码本集合其中W（g）表示第g个维的旋转DFT矩阵，G表示旋转DFT矩阵的总数，每一个矢量可以表示为[28]。

3.2 码本弦距离特性分析

弦距离可以衡量2个矢量的相似度，2个矢量的弦距离计算式[29]为

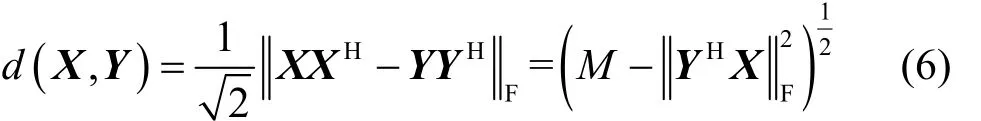
其中，X、Y表示相同维度的矢量，表示求解F范数。当子空间维度M=1时，子空间求解问题转化成格拉斯曼空间装箱问题。此时，求解F范数变为求解绝对值，式（6）可简化为

1） 同一矩阵的不同列向量之间的关系

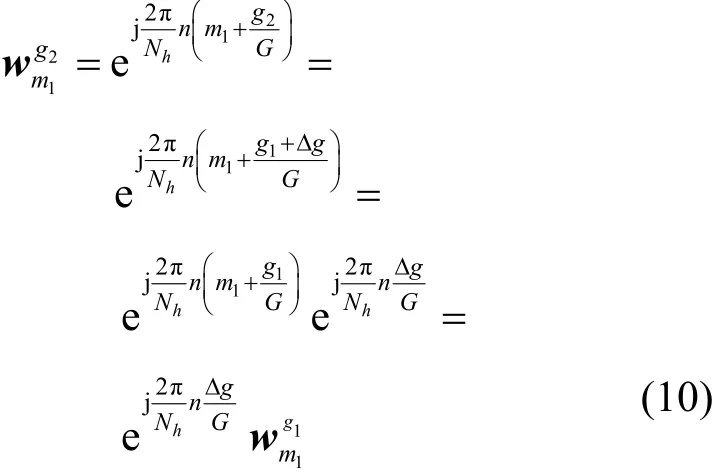
其中，Δg为矩阵编号的差值。分析式（10）可以看出，不同矩阵的相同列向量的对应元素之间的关系只与Δg有关，故和间的弦距离只与Δg有关，当Δg增大时，和间的弦距离随之增大。

由式（11）可以看出，不同矩阵的不同列向量的对应元素之间的关系与Δm和Δg都有关。故和间的弦距离与Δm和Δg有关，当Δm和Δg增大时，和间的弦距离也随之增大。

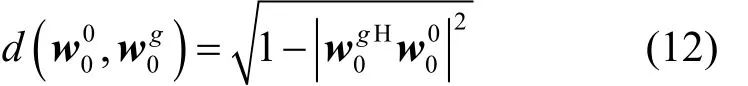
其中，g=0,1,...,31，表示第g+1个矩阵的第一列。

码本向量间的弦距离可以衡量2个向量的相似程度，弦距离越小的2个向量的特性越接近。根据上述向量关系和弦距离分析，以包含32个矩阵的旋转DFT码本为例，第一个矩阵的第一列和第五列与其他所有码本向量的弦距离特性如图 2所示。

从图2（a）可以看出，第一个矩阵的第一列与其他矩阵的第一列的弦距离最小，并且随着矩阵编号的增大，弦距离随之增大。从图2（b）可以看出，第一个矩阵的第五列与其他矩阵的不同列之间的弦距离与图2（a）类似。经过仿真分析，码本集合的所有码本向量均有如图2所示的特性，矩阵编号不同的码本相同列间的向量弦距离最小。同时，矩阵编号相差越小的码本相同列间的向量弦距离越小。

图2 旋转DFT码本的特性分析

通过对弦距离特性的分析可知，为了保证每组内的任意 2个矩阵的对应列的码本向量的弦距离尽量小，分组越多越好。但是分组越多越接近遍历搜索算法，导致搜索复杂度越高。本文中把码本集合的32个矩阵分为2组和4组进行码本向量的弦距离特性分析。根据式（12）和式（13）分别计算分组后第一组第一个矩阵的第一列与该组内其他矩阵相同列和不同列的向量间弦距离。当分组数为2时，每相邻的16个矩阵属于一个组（组内矩阵编号的设置是 1,2,…,16，即g=0,1,…,15）。当分组数为4时，每相邻的8个矩阵属于一个组（组内矩阵编号的设置是1,2,…,8，即g=0,1,…,7）。分组后的第一组内的第一个矩阵的第一列向量与本组内所有码本向量的弦距离特性如图3所示。

如图 3（a）所示，当分组数为 2时，该组的第一个矩阵的第一列与本组的所有矩阵的第一列的预编码向量的弦距离都比与其他列的预编码向量的弦距离要小，最大的弦距离不超过0.75。如图3（b）所示，当分组数为4时，各列弦距离具有与上述类似特性，最大的弦距离不超过0.4。通过对所有组的码本向量进行研究发现，不仅是第一组，其余分组也有一样的特征，即码本集合中每组中矩阵的相同列之间的弦距离比与其他列的弦距离小，即相同列具有非常相似的特性，对信道的匹配性能也更为接近。

图3 旋转DFT码本分组后的特性分析

3.3 码本搜索方法设计

根据前述码本特性的分析，设计了一种基于分组的低复杂度的码本搜索方法。以32个码本分为4组为例，水平维码本搜索的具体步骤如下。

步骤1将32个码本矩阵分成4组，每组8个相邻的矩阵，表示为Ωi，如式（14）所示。

步骤 2在每组的第一个矩阵中选择最佳预编码矢量，即获得最大化信道增益

步骤3根据获得的所在矩阵的列数Ij，计算每组中各码本该列码字的信道增益，在每组中选择最优预编码矢量。

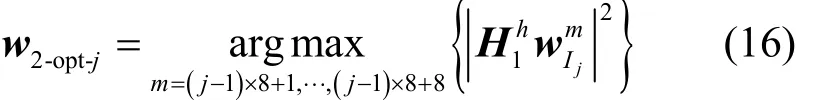
其中，Ij表示每组第一个矩阵获得的最佳码字所在的列数，并且i=j= 1,2,3,4。由于分组中的每个码本只涉及一个列向量的信道增益计算，从而可以大大降低计算复杂度。

步骤 4在中选取最佳水平维度预编码矢量wh，如式（17）所示。

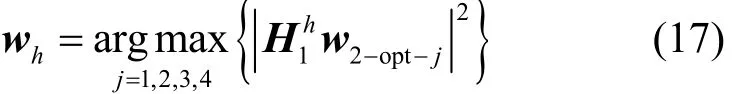
对于垂直维度码本，采用与上述步骤相同的搜索算法得到最优的垂直维度预编码矢量wv，并且在搜索过程中用到相应的垂直维度子信道最终在基站端获得的预编码向量为

3.4 复杂度分析

以本文涉及的码本尺寸（32个8×8码本）为例分析遍历搜索方法和本文所提出的搜索方法的复杂度，搜索代价主要考虑信道增益的计算次数。若采用传统的码字搜索方法，水平维度和垂直维度要分别进行32×8=256次列向量与信道向量的计算并进行比较，搜索代价为本文提出的搜索方法，水平维度和垂直维度分别进行搜索，搜索代价为其中n1为一个DFT矩阵的列数，n2为每组的矩阵个数，n为组数）。由此可知，本文提出的方法搜索代价仅为遍历搜索方法的大大地降低了搜索的代价。

搜索复杂度如图4所示。其中，图4（a）表示不同发射天线数且分组数为4时2种算法的搜索复杂度，图4（b）表示不同分组时的搜索复杂度。

从图 4（a）可知，基站配备天线数Nt为 2×2、4×4、8×8、16×16时，本文提出的码本搜索方法与经典的遍历法相比可以有效地降低码本搜索的计算复杂度，并且随着基站端天线数目和码本数量的增加优势更明显，因此本文提出的搜索方法更加适合大规模MIMO的应用场景。由图4（b）可知，搜索复杂度与码字分组数目n有关。随着码字分组数目的增加，搜索的复杂度增加。但分组数目较多时与信道更匹配，具有较好的性能增益；码字分组数越少，搜索复杂度就会越低，但是同一列的向量的弦距离会变大，与信道的匹配性能减弱，影响系统性能。因此需要权衡搜索复杂度与系统性能来确定分组数目。

图4 搜索复杂度比较

4 仿真结果与分析

仿真所使用的信道模型为3D winner 2信道模型[30]，基站端采用8×8的均匀平面天线阵列，用户端配置两天线，天线间的间距为半波长。在发送端使用QPSK（quadrature phase shift keying）调制，假设为理想信道估计，接收端采用 MMSE（minimum mean square error）方法解调信号。图 5（a）和图5（b）分别给出了不同码本组合与不同搜索方法的误码率性能。本文方法与遍历搜索方法的容量比较如图6所示。

由图5（a）可知，与其他码本相比旋转DFT码本更适合相关信道，即旋转DFT码本在大规模MIMO中可以提供更好的性能。DFT码本虽然适合强相关信道，但是由于码本数量很小，对信道的匹配度很低，性能最差。爱立信码本由于在单层传输时码本数量较小而不能获得很好的性能增益。R11单层传输码本的码本数量为 256，与具有相同码本数量的旋转DFT码本相比，性能明显不如旋转DFT码本的性能。从图5（b）可知，与遍历搜索方法相比，本文的搜索方法会带来一定的性能损失，但随着分组数量的增大，其性能差别越来越小。首先，由于本文方法依据弦距离特性进行码本搜索，并且码字间弦距离随着矩阵编号的增大逐渐增大，导致码字间的相似性随之降低，对信道的匹配程度变差，因此该方法会有一定的性能损失。其次，不同分组数的误码率性能不同。这是由于分组数越少，组内的码本数量越多，码字间的弦距离差距越大，导致与信道的匹配性能下降，带来了一定的性能损失。反之，分组数越多时性能越接近遍历算法。

图5 误码率性能比较

由图6可知，本文的搜索方法获得的系统容量接近遍历搜索方法获得的系统容量，并且分组数为4时的性能优于分组为2时的性能。进一步结合图4（b）分析，权衡搜索复杂度与系统性能，当矩阵的个数为32时，得到最佳分组数为4。

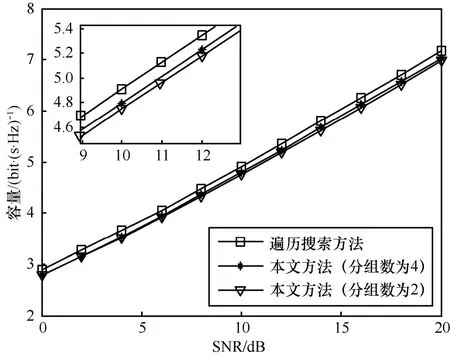
图6 不同搜索方法的系统容量

5 结束语

本文针对适合大规模 MIMO系统的旋转DFT

码本组合提出了一种低复杂度的最优码字搜索方法。仿真结果表明该搜索方法在保证系统性能的前提下有效降低了搜索复杂度，从而降低了5G网络中用户终端的设计要求。同时，本文所提搜索方法的优势随着天线数目的增加变得更加明显，因此该方法更加适合大规模MIMO的应用场景。本文方法对于具有此类弦距离特性的码本具有适用性，对于其他类型的码本同样可以根据其结构特性利用本文分组的思想来设计搜索方法。在进一步的研究中，将考虑将码本搜索方法与码本设计结合，根据所设计的码本特性进行码本搜索。