基于布尔混沌的物理随机数发生器

张琪琪，张建国，李璞，郭龑强，王云才

（1. 太原理工大学新型传感器与智能控制教育部山西省重点实验室，山西 太原 030024；2. 太原理工大学物理与光电工程学院，山西 太原 030024）

1 引言

随机数被广泛应用于蒙特卡洛仿真、深度学习、身份认证、密码学等领域[1-4]，尤其在密码学中，不可预测、统计无偏的物理随机数是确保加密信息安全的关键。

目前，很多随机数发生器（RNG，random number generator）是通过计算机或微处理器运行某种确定性的数学算法（如线性同余、线性反馈移位等）来产生伪随机数；但伪随机数具有周期性，存在可被预测的安全隐患，因此伪随机数发生器（PRNG，pseudo-random numbers generator）难以确保加密信息的安全。

与PRNG不同，物理随机数发生器（Physical-RNG，physical random number generator）可以产生无周期、不可预测的物理随机数，这对于数据加密技术来说，是真正安全的。目前，Physical-RNG主要利用不可预测的物理随机过程作为熵源（也称为物理熵源）来产生随机序列，例如电路中的热噪声[5]、振荡器的相位抖动[6]及非线性系统中的混沌[7]等。电路热噪声Physical-RNG由于热噪声幅度较小，需要高增益运算放大器进行放大，而放大器不仅功耗大，其有限的带宽和失调还会使Physical-RNG 的随机特性变差。振荡器Physical-RNG利用低频时钟源的随机相位抖动来获取随机数序列，然而该技术存在随机数产生速率较低的不足。混沌是由非线性系统产生的一种类噪声信号，它具有对初值敏感、不可预测等特点[8]，因而在Physical-RNG设计中得到了广泛的应用，如利用离散混沌迭代[9]、时空混沌[10]、多混沌系统耦合[11]、无简并高维离散超混沌[12]等方法都可以产生高质量的随机数。然而，上述混沌系统都属于数字混沌系统，存在混沌退化效应[13]，其产生的随机数本质上都是伪随机的[8-13]。

2013年，一种结构简单的可集成式 Physical-RNG被报道，该方法利用带有自反馈结构的自治布尔网络作为物理熵源，实现了速率为100 Mbit/s（单个 Physical-RNG 单元）的物理随机数产生[14]。但是自反馈结构会引入相关性，使得该物理熵源使用了较多、较复杂的节点（16个三输入逻辑门）以保证产生足够的熵值。

本文提出并实验验证了一种无自反馈结构的自治布尔网络物理熵源，它由多个二输入异或门节点组成。在文中，使用了节点数量为 15的网络结构，产生了带宽达680 MHz，最小熵接近于1的布尔混沌信号。利用该熵源构建的Physical-RNG具有实时速率为100 Mbit/s（单个Physical-RNG单元）的物理随机数产生能力。相比于文献[14]，本方法具有两项突出优势：1） 物理熵源结构更为简单，最少可由15个节点组成；2） 所提出的Physical-RNG拥有更低的功耗，这是因为在电路制造过程中，二输入逻辑门比三输入逻辑门使用更少的晶体管（约为三输入逻辑门使用数的一半），而较少的晶体管意味着更低的功耗。随机性测试结果表明，本方法产生的物理随机数序列可成功通过NIST SP800-22及DIEHARD所有测试项，因而具有良好的随机统计特性。

2 布尔混沌物理熵源

2.1 无自反馈结构的自治布尔网络特征

本文提出的无自反馈结构的自治布尔网络由N个节点（二输入逻辑门）组成，其结构如图1所示，N个节点以双向耦合连接方式组成环状拓扑结构。在该网络中，N-1个节点执行异或（xor）运算，一个节点执行异或非（xnor）运算。经数值仿真，发现所设计的自治布尔网络存在2种状态：振荡状态与非振荡状态。当自治布尔网络中节点数量是3的倍数时（即N=3n，n为正整数），该网络进入振荡状态；否则进入非振荡状态，即进入所谓的布尔固定点[15]。

为了验证上述情况，在FPGA中搭建了节点个数分别为N=3,4,5,…,11的自治布尔网络，并通过观测xnor的电压输出来判定网络状态。实验结果如图2所示，当N=5,7,8,10,11时，xnor的输出电压保持恒定，表明网络进入了布尔固定点；当N= 6,9时，xnor的输出电压持续变化，表明网络处于振荡状态。但是需要说明的是，实验中当N= 3时，网络并未进入振荡状态，与仿真结果不符，其原因是如下。1） FPGA中的逻辑门并非响应速度无限快的理想器件，无法响应变化速度过快的信号，即存在所谓的低通滤波效应[15-16]。2） 自治布尔网络处于振荡状态时，其振荡频率f与节点数量N成反比。当N=3时，振荡频率f较高，高频振荡信号无法被网络中的逻辑门节点响应（即低通滤波效应），因此振荡信号被衰减和抑制，导致振荡停止，如图2（a）所示；而随着节点数量N的增加（如N= 6,9,…），自治布尔网络的振荡频率f逐渐降低，当f小于低通滤波效应的截止频率时，自治布尔网络表现出持续振荡，如图 2（d）和图 2（g）所示。

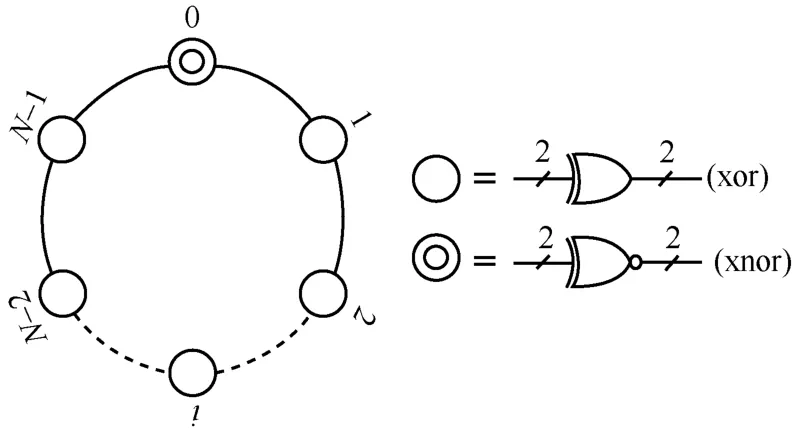
图1 二输入逻辑门节点组成的自治布尔网络

图2 N分别为3～11时节点自治布尔网络中xnor输出电压时序

2.2 布尔混沌的产生及动力学行为

布尔混沌是由自治布尔网络电路产生的一种幅值呈二值变化（逻辑高电平和逻辑低电平），触发时间（相邻2个上升沿的时间间隔）呈混沌变化的信号。其产生的动力学原因是自治布尔网络中电子逻辑器件固有的非理想特性，包括低通滤波效应、退化效应等[15-16]。

经2.1节分析可知，所设计自治布尔网络要保持振荡状态，其节点个数必须满足N=3n（n为大于或等于 2的正整数）。本部分从最大李雅普诺夫指数与最小熵这2个方面进一步分析了振荡状态下自治布尔网络的动力学特性。参照文献[17]，计算了N≥6时自治布尔网络输出信号的最大李雅普诺夫指数（λmax）。如图 3所示，λmax均大于 0，表明这些网络均产生了布尔混沌信号[18-19]。进一步研究发现，随着节点数量N的增加，布尔混沌信号的最大李雅普诺夫指数也随之增大，当N≥12时，最大李雅普诺夫指数达到极大值，之后其变化趋势逐渐平稳；因此，为了产生高质量的布尔混沌信号，应选取N≥12的自治布尔网络。同时，利用最小熵对所产生布尔混沌的随机特性进行了分析，最小熵接近于1则表明布尔混沌信号完全随机且独立同分布，适合作为 Physical-RNG的物理熵源。实验测量了N≥6时布尔混沌信号的最小熵，实验结果如图 3所示。从图中可观察到，当自治布尔网络的节点数N≥15时，所产生的布尔混沌信号的最小熵趋近于1，之后趋势逐渐平稳，因此，作为 Physical-RNG的物理熵源，应选取N≥15的自治布尔网络。

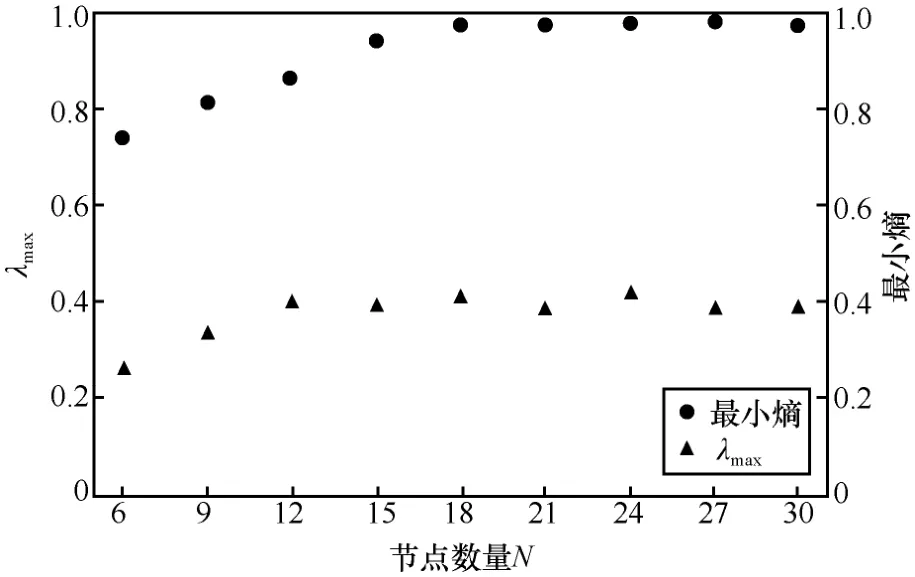
图3 自治布尔网络（N≥6）的最大李雅普诺夫指数与最小熵

2.3 布尔混沌物理熵源特性

根据2.2节分析结果，同时考虑到自治布尔网络的最优功耗，选择N= 15的自治布尔网络作为Physical-RNG的熵源。熵源产生的布尔混沌信号的时序曲线、频谱曲线和自相关曲线如图4所示，从图4（a）中可以看出，布尔混沌信号的电压呈现大幅度随机起伏（约2 V）；从图4（b）中可以看出，布尔混沌信号的频谱平坦且带宽达680 MHz；从图4（c）中可以看出，布尔混沌信号的自相关曲线的半高全宽（FWHM，full width at half maximum）约为1 ns。较宽的频谱与较短的自相关时间表明可以从该物理熵源中提取高速物理随机数序列。

图4 自治布尔网络（N=15）产生的布尔混沌信号特性

3 物理随机数发生器

本文设计的基于布尔混沌的物理随机数发生器结构如图5（a）所示，由两部分构成：物理熵源和熵提取电路。物理熵源以节点个数N=15的自治布尔网络构成，布尔混沌信号可以由其中任意节点输出。熵提取电路由一个三输入xor逻辑门和3个D触发器构成，其工作原理如下：由3个D触发器对节点0、节点6和节点9输出的混沌序列进行采样，所采样样本再经异或处理以减少物理随机数中的偏差和相关性，最终产生物理随机数序列。

该Physical-RNG已在FPGA（芯片型号：Altera Cyclone IV FPGA，EP4CE10F17C8N）中进行了实验验证，仅需16个逻辑单元（LE，logic element）即可实现，消耗资源极少。实验中，利用FPGA的PLL（phase locked loop）单元产生100 MHz信号作为D触发器的时钟，此时该Physical-RNG的随机数实时产生速率为100 Mbit/s，图5（b）为实时产生的随机比特序列。值得一提的是，以目前中等规模FPGA芯片的容量及规模（如Cyclone V 的LE单元数量为3×105左右[20]），其内部可以同时构建数万个该Physical-RNG结构，此时物理随机数的实时产生速率可至太比特每秒量级，因此，本技术在海量随机数应用领域有着广阔的发展前景。

图5 实时速率为100 Mbit/s的物理随机数发生器及产生的信号

4 随机性测试

为了评估基于布尔混沌的 Physical-RNG产生随机序列的随机性，应用了2种国际通用的随机性测试检验标准，分别为 NIST SP800-22[21]和DIEHARD[22]，测试的物理随机数样本量均为1 Gbit。NIST SP800-22由美国标准局发布，包含15项统计测试，每项测试均会针对测试本文数据生成一个P值，测试需要1 000组数据，每组数据为1 Mbit。DIEHARD由George Marsaglia发布，包括18项测试，其中少数测试重复不同的参数多次测试，每项测试均会生成一个P值，如果测试项有多个P值，则利用KS检验生成一个综合P值作为最终测试结果。在NIST SP800-22检验标准的15项测试中，设置显著水平值为α=0.01，当P值大于0.000 1，通过P值百分比大于0.980 6时，则表示通过该项测试。在DIEHARD检验标准的18项测试中，设置显著水平值为α=0.01，当每项测试的P值大于0.01且小于0.99时，则表示通过该项测试。2种检验标准的测试结果分别如表1和表2所示，所测试的物理随机数序列均通过NIST SP800-22及DIEHARD所有测试项，这表明该Physical-RNG产生的物理随机序列具有良好的随机统计特性。

表1 NIST SP800-22检验标准测试结果

5 结束语

本文提出并实验验证了一种基于自治布尔网络的宽带物理混沌熵源，并基于该熵源构建了实时速率为100 Mbit/s 的物理随机数发生器。随机性检测结果表明，物理随机数发生器产生的随机数序列可以通过NIST SP800-22检验标准和DIEHARD检验标准，具有良好的随机统计特性。此外，值得一提的是，基于该熵源设计技术，可以在FPGA中构建出速率更高的随机数发生器；这是由于该熵源仅需 16个 LE即可实现；因此在

表2 DIEHARD检验标准测试结果

FPGA中可以大规模部署，达到多熵源并行产生高速随机数的效果。以目前Altera公司中低端FPGA

芯片Cyclone V 为例，其LE单元数量在3×105左右，因此可以在芯片内部同时构建数万个本文提出的物理熵源，实现太比特每秒量级的高速物理随机数实时在线产生。未来，本技术在高速随机数发生器应用领域将有着广阔的发展前景。