深度置信网络拟合异步电动机逆变器控制开关表
2019-02-25单文丽钱慧敏卢新彪段朝霞黄浩乾
单文丽,周 军,钱慧敏,卢新彪,段朝霞,黄浩乾
(河海大学,南京 211100)
0 引 言
在各控制工程领域,与机械、电力电子或机电一体化等传统形式的硬件控制器相比,基于机器学习及其算法的软硬混合控制器越来越显示出独特的优势。目前,在机器学习研究中影响较大的是Simon H的观点:机器学习能力对系统任何技术的改进、改良都是有必要的, 这种学习能力的获得使得机器系统在重复性极强的工作或类似关联性的工作时,完成得更好,有更出色的表现。
近年来,深度学习在学术界和工业界都得到广泛关注,取得了迅猛发展。如深度学习在模式识别上取得了比一般神经网络学习的识别率有显著提升的效果[4]。深度学习神经网络在算法构造上有更多的隐藏层和大量神经元,这样就大幅度提高了网络学习的复杂度和自由度,从而提高了可拟合复杂关系的范围和高度。一些无法由浅层人工神经网络解决的大规模、复杂问题可以由深度学习算法来解决。深度学习已被应用到各种工程问题中,包括特征分类[1]和模式识别[2]。例如:语音识别[3],手写体数字识别,人体行为识别[4]等。利用深度学习算法对复杂函数拟合能力[4-7]的研究多有报告,但利用深度学习算法代替经典控制器的控制策略进而形成神经网络控制器实际实施控制的研究报告不多[8-9]。本研究旨在通过使用DBN(deep belief network)算法来模拟经典直接转矩控制电路里的开关表控制效果,验证深度学习算法用于替代硬件控制器的可行性和有效性[8,10]。具体地,以调整转子速度和角度来驱动加工部件实现位置、进度等控制目标的异步电动机系统为例,使用MATLAB/Simulink进行数值仿真,研究和比较深度学习控制器和经典直接转矩控制里开关电路控制效果,证明了深度学习控制器的性能和有效性。
1 深度学习算法概述
深度学习概念最早出现在2006年,由Hinton G E等学者[7]一起提出的复杂神经网络算法。这种算法依赖于样本数据,通过一定的训练方法得到每一层神经元所构成的结构拓扑和权值参数[11]。Hinton等为了解决传统的神经网络产生局部最小值的问题,找出传统神经网络陷入局部最小值的根本原因,即训练算法中权值初始化是随机的,只需要采用无监督的预训练方法优化网络权值的初值, 再进行有监督的权值参数微调的学习方法。这种参数微调通常使用反向传播算法(以下简称BP算法),微调整最后一层的权值和偏置。总之,深度学习是从单层或浅层神经网络中扩展出来的算法,是基于隐藏层和神经元的数目众多的深度神经网络的,这使得深度学习算法拥有高维参数(包括权值和偏置),从而可拟合非常复杂的函数关系。然而,层次结构和神经元个数的增多,也同时会在神经网络学习过程中使函数被过度拟合,生成预训练也使得多层次特征检测变得更为复杂。这种算法特征使得深度学习网络与浅层神经网络之间的区别明显,并具有复杂结构的独特特性。典型的深度置信网络(以下简称DBN)是各种深层学习网络中比较著名的。以下关于DBN算法的简要说明是为了便于理解深度学习的各过程。
1.1 DBN的构成与算法
DBN通常是由多个受限玻尔兹曼机(以下简称RBM)交互堆叠而成[11-12],如图1所示(图1中是三重RBM形成的深度网络,以下说明中为保持符号关系简明,均以此为例)。该类神经网络进行从输入端到输出端的前向运算时,输入数据从输入层的RBM输入网络,之后经逐层RBM向前运算,到达网络的输出层后,形成神经网络整体的输出。
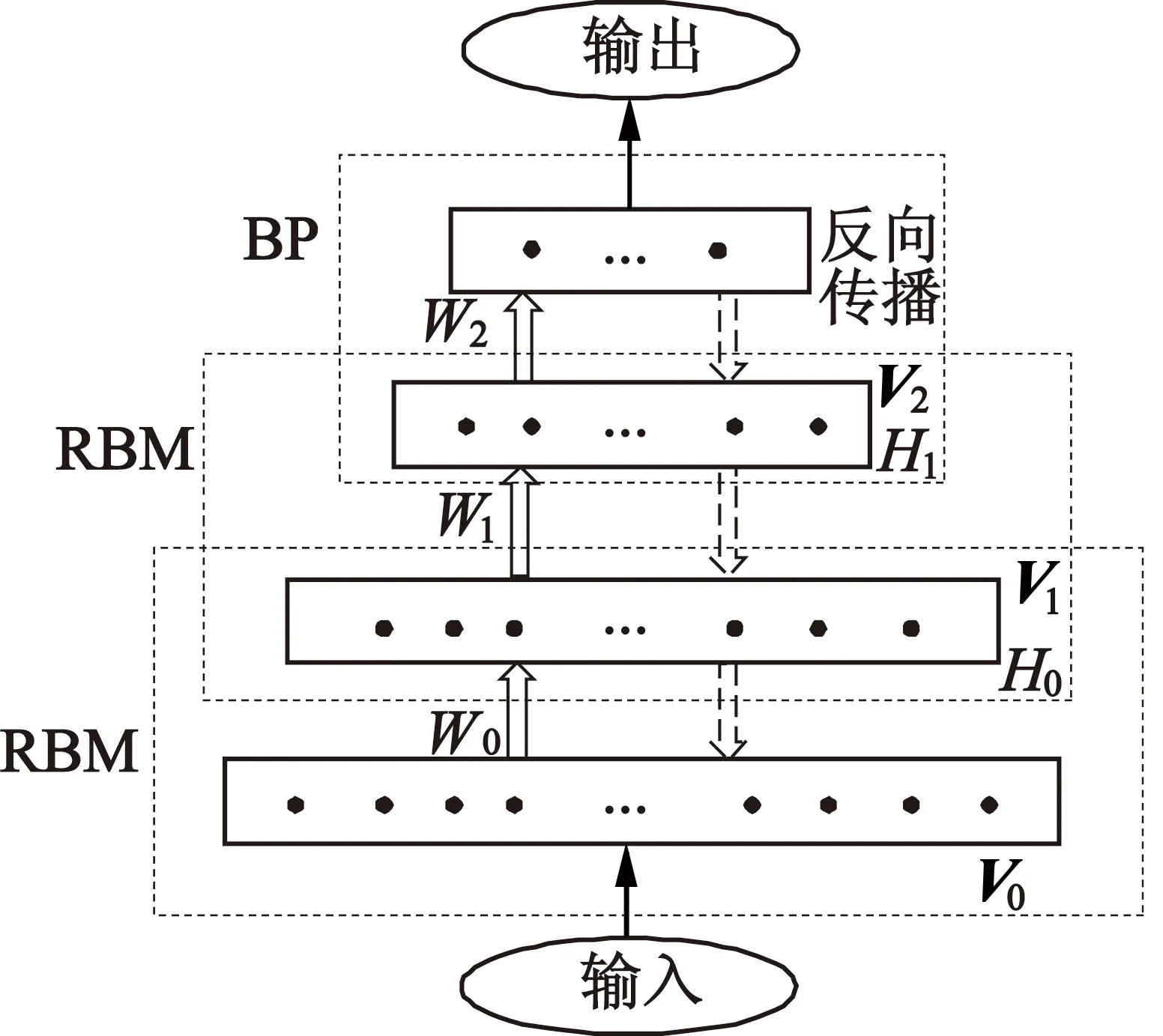
图1 DBN的构成框架
标准的DBN算法[13]包括有两个基本过程:各RBM模型基于无监督学习的初始连接权值和偏置的预训练(即图1中由实线双箭头表示的方向与过程)以及基于BP的全局微调(即图1中由虚线双箭头表示的方向与过程)。具体如下:
第一过程:进行DBN前向计算,完成各RBM连接权值与偏置的预训练。具体地,输入数据(参考向量)进入第一层RBM的可见层,结合初始前置权值(即第一层RBM的可见层前面的权值)将向量V0转换并转移到该RBM隐藏层,按照Boltzmann分布随机生成该隐含层的前置权值修改量,进而修改权值。其中,RBM的预训练是由CD(Contrastive Divergence)算法完成。由图1可知,第一层RBM的隐藏层也是第二层RBM的可见层,由此,第一层RBM的输出数据作为第二层RBM的参考输入向量就传递给了第二层RBM的可见层,并结合第二层RBM的可见层前置权值转换并传递到第二层RBM的隐藏层,重复第一层RBM的前置权值修改过程,完成第二层RBM的预训练。以后诸层依次重复,直至整个网络的前向运算结束。这样就得到了下面第二过程的全局微调的初始连接权值(即各层RBM的前置权值与偏置)。
第二过程:完成针对神经网络最后一层RBM至第一层的基于BP算法的反向连接权值微调,从而完成DBN整体微调。如图1所示,在DBN的最后一层RBM中开始反向传播,把当前层RBM的输出向量反向作为输入向量,对比理想的输出向量, 通过偏差极小化等算法来实现该层RBM的权值微调。与此相对,也有通过逐层BP算法进行多层微调整个DBN的,但这样的反向传播会将错误信息自顶向下传播至所有RBM。本文只考虑对最后一层(即图1的最顶层)RBM进行BP算法的权值微调,所以误差反向传播问题不会发生。
下面针对DBN的参数预训练和微调中的连接权值修正关系公式等给出具体说明。
1.2 DBN的预训练
DBN中的每层RBM是一个完整且独立的神经感知器,每一个RBM都有可见层和隐藏层,连接它们的神经元为双向全连接,其连接权值基于Boltzmann随机分布进行增量调整。为叙述方便,考虑一个共有n个神经元层的DBN,其各神经元层分别称为第l层,各层神经元个数分别为m1,m2,…,mn个,各神经元激活函数均为sigmoid(z)=(1+e-z)-1=∶f(z)。又定义各层的激活函数值向量:
Rmn
(1)

Rml×ml-1
(2)
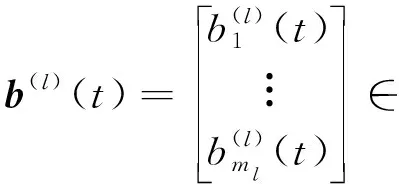
(3)
Rml
(4)
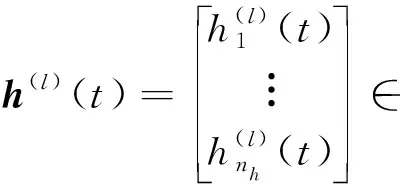
(5)
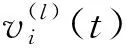
这样前向传导关系可表达如下:
z(l+1)(t+1)=W(l)(t)a(l)(t)+b(l)(t)∈Rml
(6)
(7)
即z(l+1)(t)是第l+1层神经元t时刻的状态向量。
接下来,为了刻画以第l-1层作为可见层,以第l层作为隐含层的RBM中,可见层与隐含层间的连接权值修正过程的能量变化[13],用式(8)定义的函数表示对该RBM的能量度量:
(8)
于是,网络权值的训练过程可看成是进行网络能量函数极小化的过程。
为建立连接权值的修正算法,定义所考虑层的RBM中的两层神经元的增广状态向量[v(l-1)(t),h(l)(t)]的联合分布概率(即所谓Boltzmann分布):
(9)
式中:Z定义为概率运算归一化因子,即:
(10)
在作为感知器的RBM中,隐藏层和可视层神经元均为二元取值,即每个神经元只有0和1两种状态值。考虑给定第l-1可见层的所有神经元的(随机)状态向量时,对应隐藏层(即第l层)上神经元被激活(即状态值为1)的条件概率,就是要计算P[h(l)(t)=1|v(l-1)(t)]。这里h(l)(t)=1是指所有标量元素都为1的向量。具体地,有:
(11)
同理,成立:
(12)
基于上述关系,v(l-1)(t)对隐藏层神经元状态的条件概率P[h(l)(t)=1|v(l-1)(t)]依定义可推导如下:
P[h(l)(t)=1|v(l-1)(t)]=
(13)
类似地,隐藏层神经元状态h(l-1)(t)关于可见层神经元状态的条件概率有:
P[v(l)(t)=1|h(l-1)(t)]=
(14)
假设给定可见层神经元状态时,与其相对的隐藏层神经元的激活条件是互不相关的,与之相反也成立。于是成立:
(15)
记θ={W,a,b}表示RBM中的待拟合参数的简约标记。有了上述各分布概率关系后,该RBM 的隐藏层待拟合参数{W,a,b}的获得就是一个基于给定训练数据的最大似然训练过程。假设训练样本集合S={v1,v2,…,vns},ns是样本总数。训练RBM的目标就是最大化如下似然概率函数:
(16)
注意到样本vi与时间无关,所以t时间变量在上式中并没有出现。由对数函数单调性可知,最大化Lθ和最大化lnLθ是等价的。于是训练RBM参数的目标就可以通过最大化如下函数关系完成。
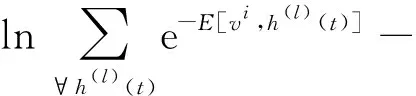
(17)
对lnLθ进行最大化的常用方法就是梯度法,即通过梯度计算迭代逼近最优点,迭代关系定义:
(18)
式中:α为学习率。另外,有:
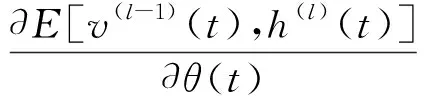
(19)
于是按照θ取ωi,j,ai,bi分别给出计算关系如下。
θ=ωi,j时的计算结果:
(20)
2)θ=ai时的计算结果:
(21)
3)θ=bi时的计算结果是:
(22)
进而,由式(19),式(20)可得:

(23)
由式(19),式(21)可得:
(24)
由式(19),式(22)可得:
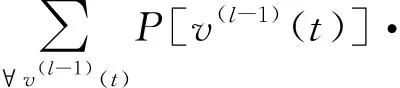
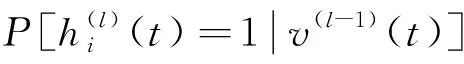
(25)
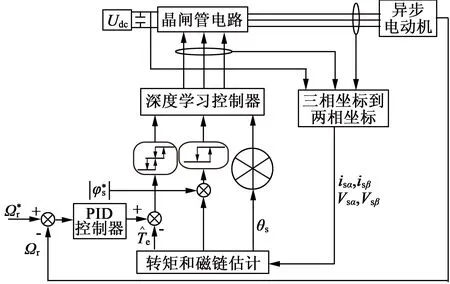
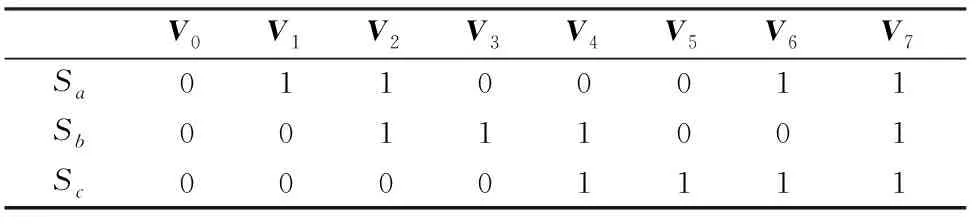
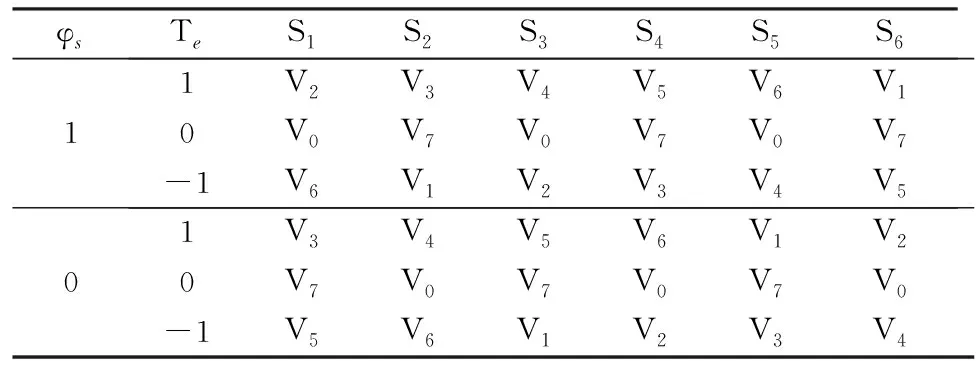
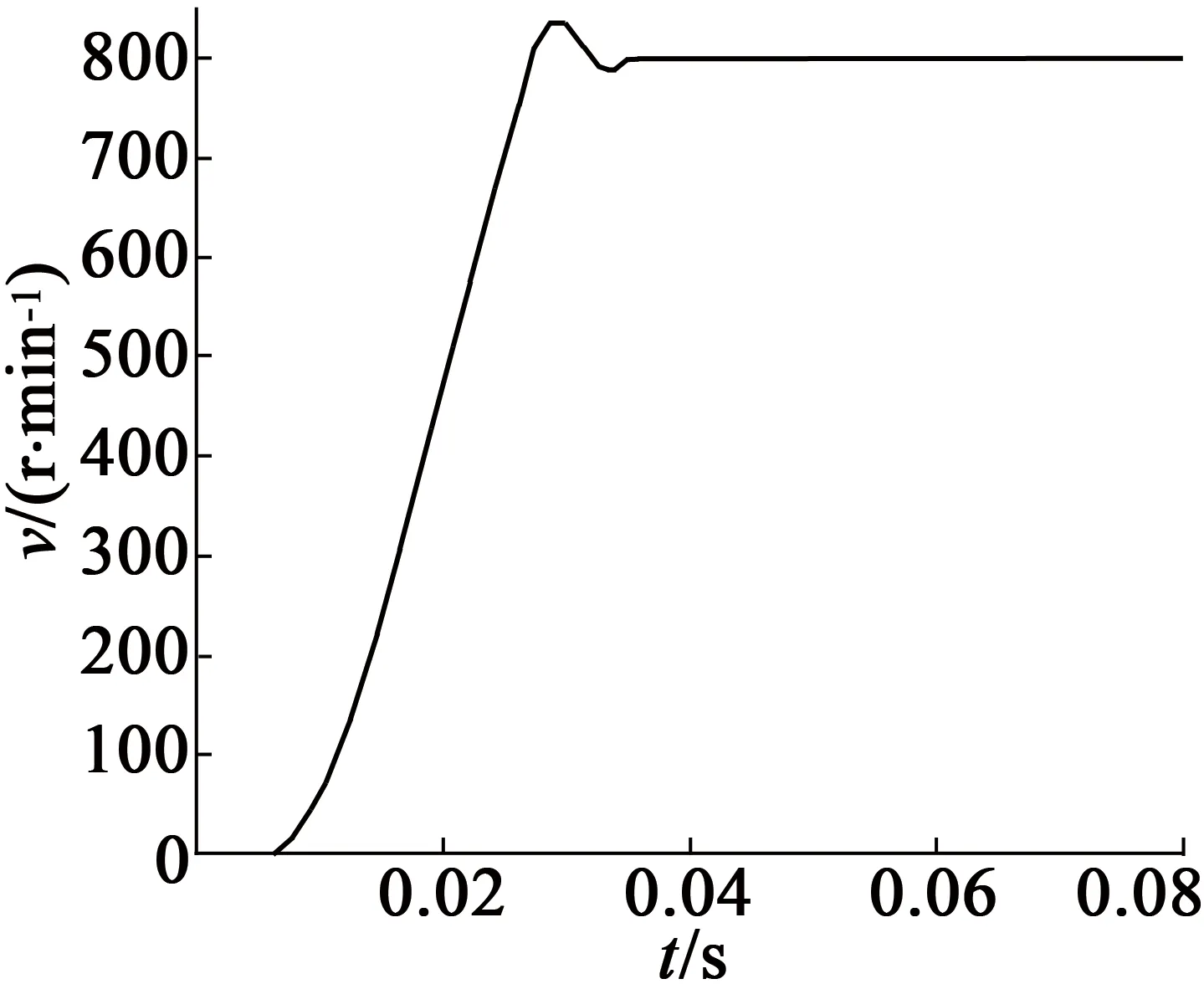
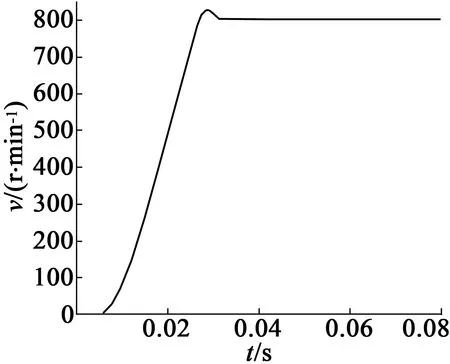
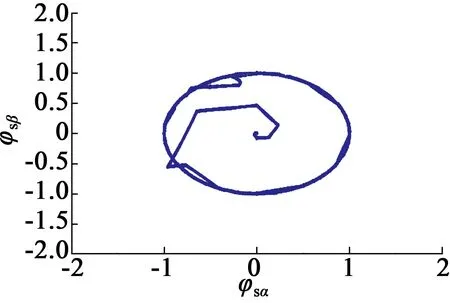
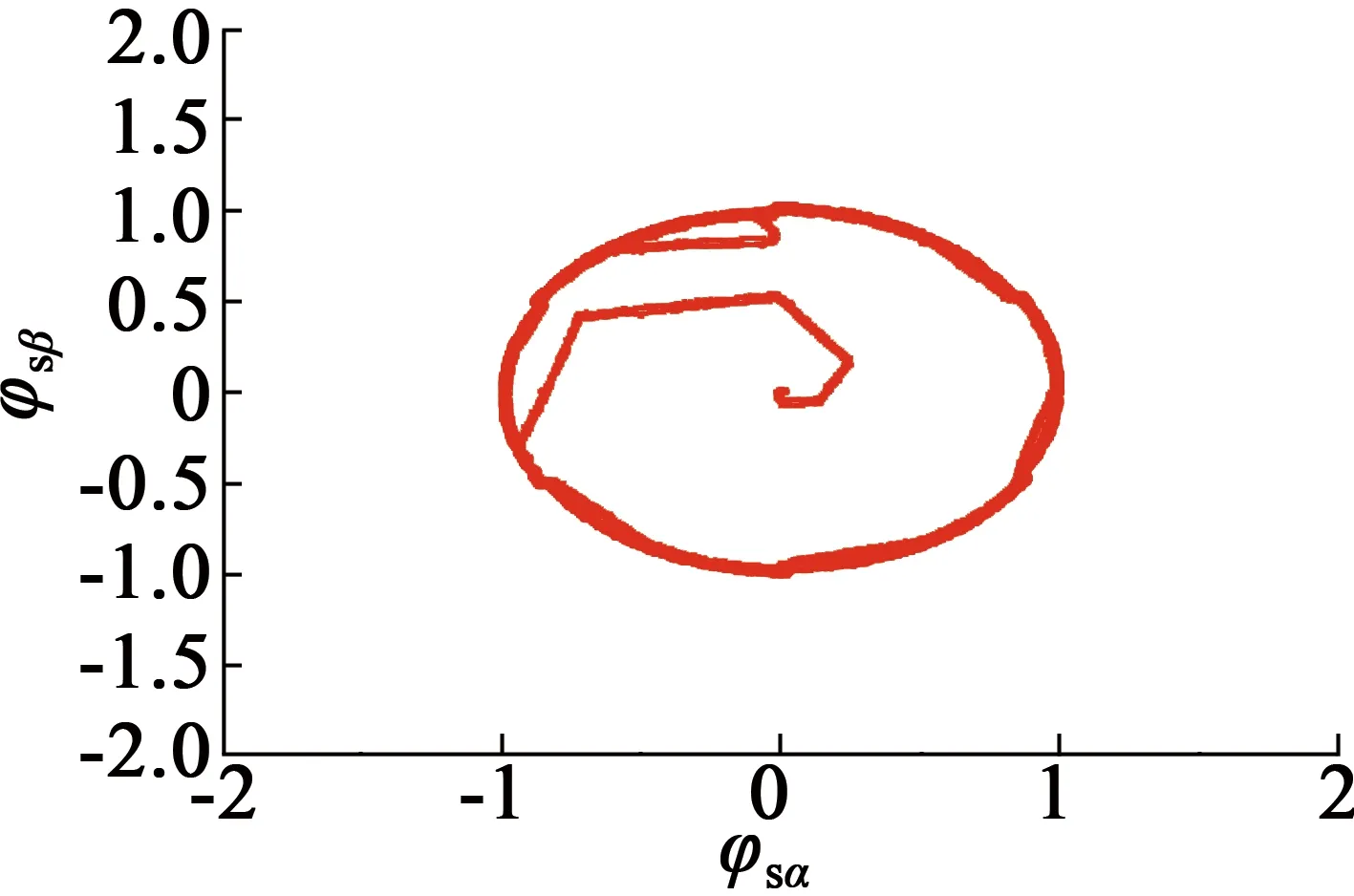
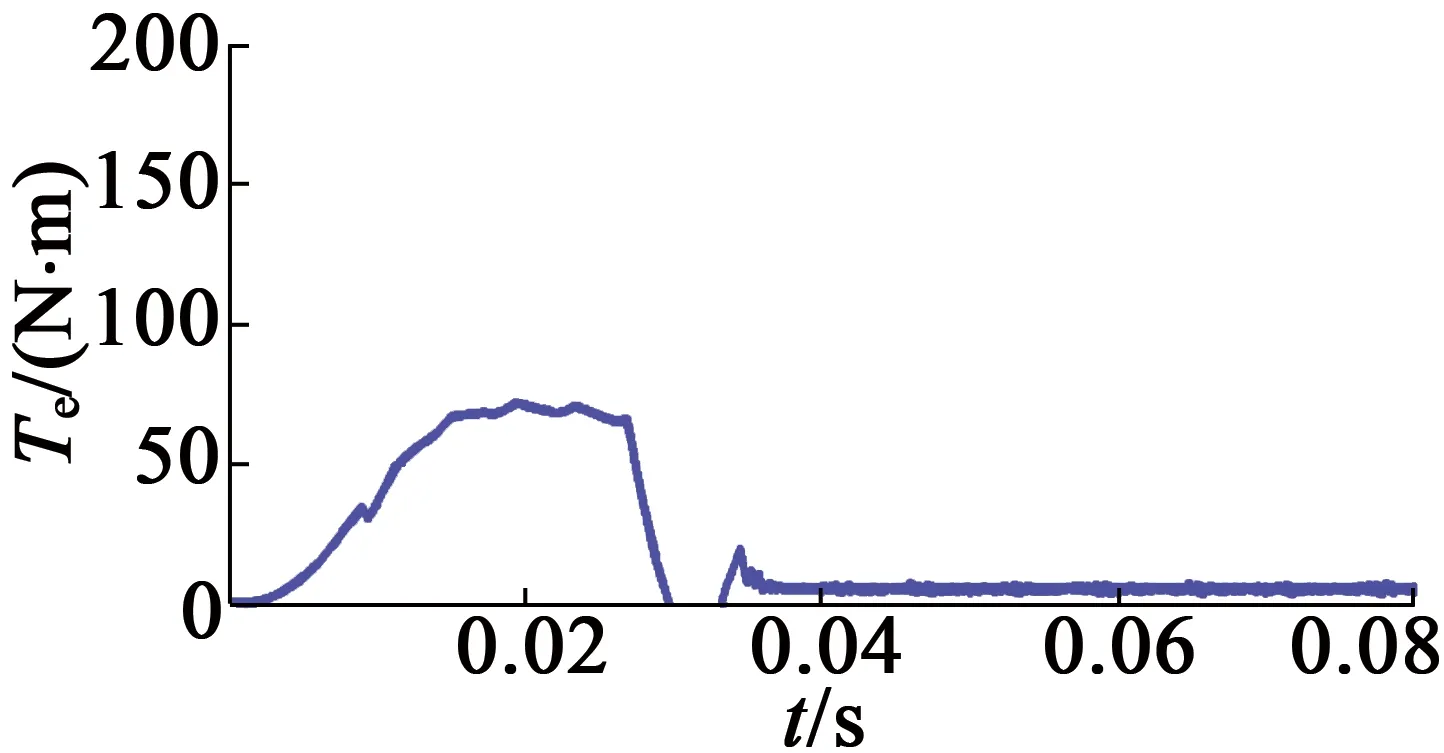
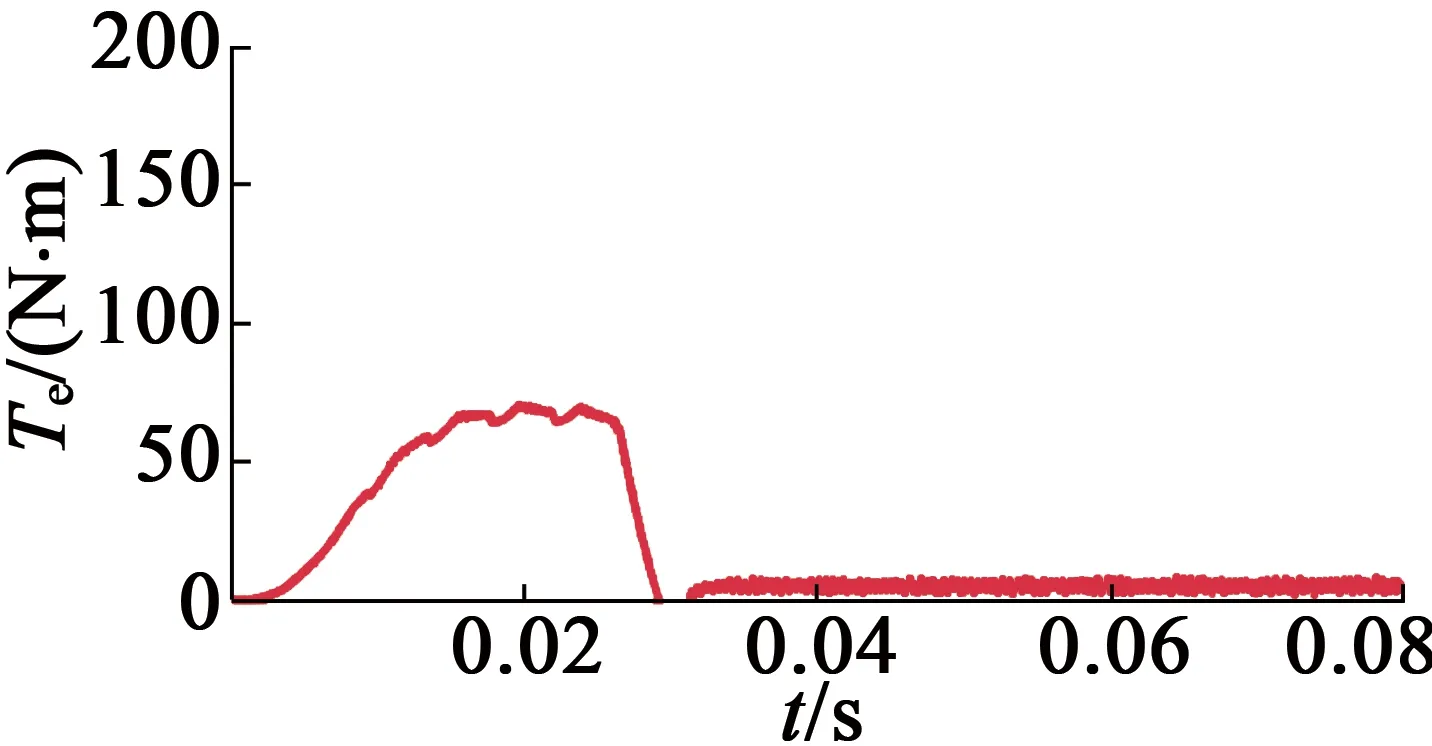
事实上,式(23)~式(25)的v(l-1)(t)是随机的,可采用对比散度算法(即k步Gibbs算法)进行采样获得。具体地,从第l层到第l+1层之间关系有:利用P[v(l-1)(t)=1|h(l-1)(t)]采样得出v(l-1)(t);利用P[h(l-1)(t)=1|v(l-1)(t)]采样得出h(l)(t),即利用rand函数产生随机数r,若r 接着,利用上述采样得到的v(l-1)(t)来近似估计式(9)~式(11)的期望项(均值项),具体如下: (26) (27) (28) 在采样取值为1,这样得到的是权值在可见层偏置和隐藏层偏置在该当意义下的修正量,从而可建立如下迭代修正关系: (29) 在上述的参数微调过程中,和传统神经网络相比,DBN算法多层RBM造成了根本性差异。显然上述修正关系RBM是无监督学习,因为过程中没有基于目标数据的参数修正部分。 DBN全局微调是BP过程,步骤如下: 对于单个样例(z,y)(指某输入样本向量z对应的期望输出值向量或目标特征数据y的关系对),其非线性代价函数定义: (30) 当进行参数微调时,训练规则将使代价函数J在每个训练循环按梯度下降。于是基于代价函数梯度计算的对参数W和b的更新迭代规则: (31) (32) 式中:ε为修正步长。 注意到式(6)的标量展开式: (33) 从而对式(33)做偏导运算后就有: (34) (35) 类似地,计算得: (36) 3) 由式(35)和式(36)可知,参数更新规则: (37) (38) 这样,式(37)和式(38)就可以给出连接权值和偏置的BP算法意义下的迭代更新值。 要设计基于DBN的深度学习控制器来替代异步电动机系统中的逆变器开关电路,首先要对原开关表进行操作和数据测量,如图2(a)所示,以得到开关表的输入和输出变量之间的关系;然后这些输入和输出信息作为深度学习算法的输入和目标数据,对深度学习控制器进行训练;最后深度学习控制器被接入电路更换原来的开关表,实现深度学习控制器控制异步电动机的目的,如图2(b)所示。 (a) 经典直接转矩控制异步电动机 (b) 深度学习替代开关表控制异步电动机 考虑开关表的工作状态如表1和表2所示。 表1 电压矢量开关选择表 表2 开关表的组合状态 因此,用深度学习控制器来代替实际的电压矢量开关表电路,首先要收集有关开关表电路的输入输出数据,直到收集的数据足以充分地反映运行关系为止。然后,DBN算法基于收集到的输入输出数据学习开关表的控制作用训练学习,完成深度学习控制器的设计。 深度学习控制器的预训练步骤如下: 步骤1:开关表样本数据的收集整理。即收集磁通、电磁转矩误差、定子磁通矢量位置和电压矢量作为DBN算法训练的参考数据和目标数据并对数据,样本进行关系标注; 步骤2:对DBN权值矩阵,偏置向量初始化。初始化矩阵的各元素均设为零; 步骤3:基于式(15)~式(17)的前向计算,得到各隐藏层的有关参数预置值; 步骤4:基于式(25)、式(26)的BP算法,对DBN网络进行单步反向调整,实现对DBN的全局微调; 步骤5:训练收敛性满足误差要求时,结束计算并给出训练结果;否则返回到步骤3再次训练。 考虑文献[8]的异步电动机数学方程如下: (39) 电磁转矩方程: Te=p(φsdisq-φsqisd) (40) 机械方程: (41) 定子磁通估计: (42) (43) 式中:Vsα,Vsβ是α,β相的定子电压;isα,isβ是α,β相的定子电流;φsα,φsβ是α,β相的定子磁通,φsd,φsq是d,q坐标下的定子磁通;isd,isq是d,q坐标下的定子电流;Rs是定子电阻;Ls是定子电感;Lr是转子电感;Lm是互感;Ts,Tr分别是定子和转子时间常数;σ是磁漏系数;J表示转动惯量;f是摩擦系数;p是极对数;v是转子转速;ω是转子角速度;Te是电磁转矩;TL是负载转矩。 表3是异步电动机各项参数的设定值。 在MATLAB/Simulink环境中,基于深度学习的异步电动机开关表进行控制拟合,研究和比较前后两种控制方法的控制效果。 深度学习算法是基于Tanaka等开发的深度神经网络工具箱的,经过修改,形成隐藏层由4层组成,共有6层神经元层的DBN,每层各包含63个神经元。本文中深度学习控制器的迭代次数为3 680,学习率为0.01。 表3 异步电动机的参数值 图3和图4分别给出了在开关表电路控制和深度学习控制器作用下的异步电动机速度响应曲线。 图3 开关表控制下的速度响应曲线 图4 深度学习控制下的速度响应曲线 图5和图6分别给出了在开关表控制和深度学习控制器作用下的异步电动机的定子磁通。 图5 开关表控制下的定子磁通 图6 深度学习控制下的定子磁通 图7和图8分别给出了在开关表控制和深度学习控制器作用下的异步电动机的电磁转矩。 图7 开关表控制下的电磁转矩 图8 深度学习控制下的电磁转矩 通过对比可知,在选择所有检测变量关系上,深度学习控制器替代原先的开关表的开关电路控制作用,可以使系统基本达到原来的控制效果,使系统镇定。由上述控制效果比较可知,深度学习控制器替代原先开关表实施控制异步电动机的方案是完全可行的。特别由DBN算法来模拟实际开关表控制的技术思路是值得理论探讨的。 本文旨在探讨基于DBN算法的深度学习控制器对控制问题的实现能力,以及开关表控制和所提出的深度学习控制器之间的比较研究,以验证深度学习控制理论对物理控制器的拟合精度。数值仿真结果表明,基于DBN算法的深度学习控制器作为传统控制器的替代方案是可行的。这种智能控制器的设计思路是,先基于基本控制理论设计控制器的结构与策略,然后基于神经网络对控制器的控制策略的学习与模仿形成基于神经网络算法的控制策略,将神经网络算法替代原理论设计的决策环节后,与硬件执行器一并形成智能化控制器。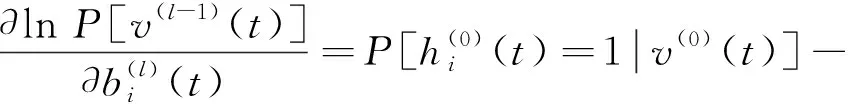
1.3 DBN的全局微调
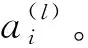
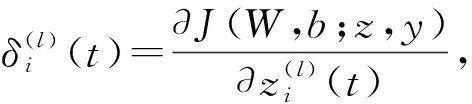
2 深度学习控制器替代开关表及其在异步电动机的应用与仿真
2.1 深度学习控制器
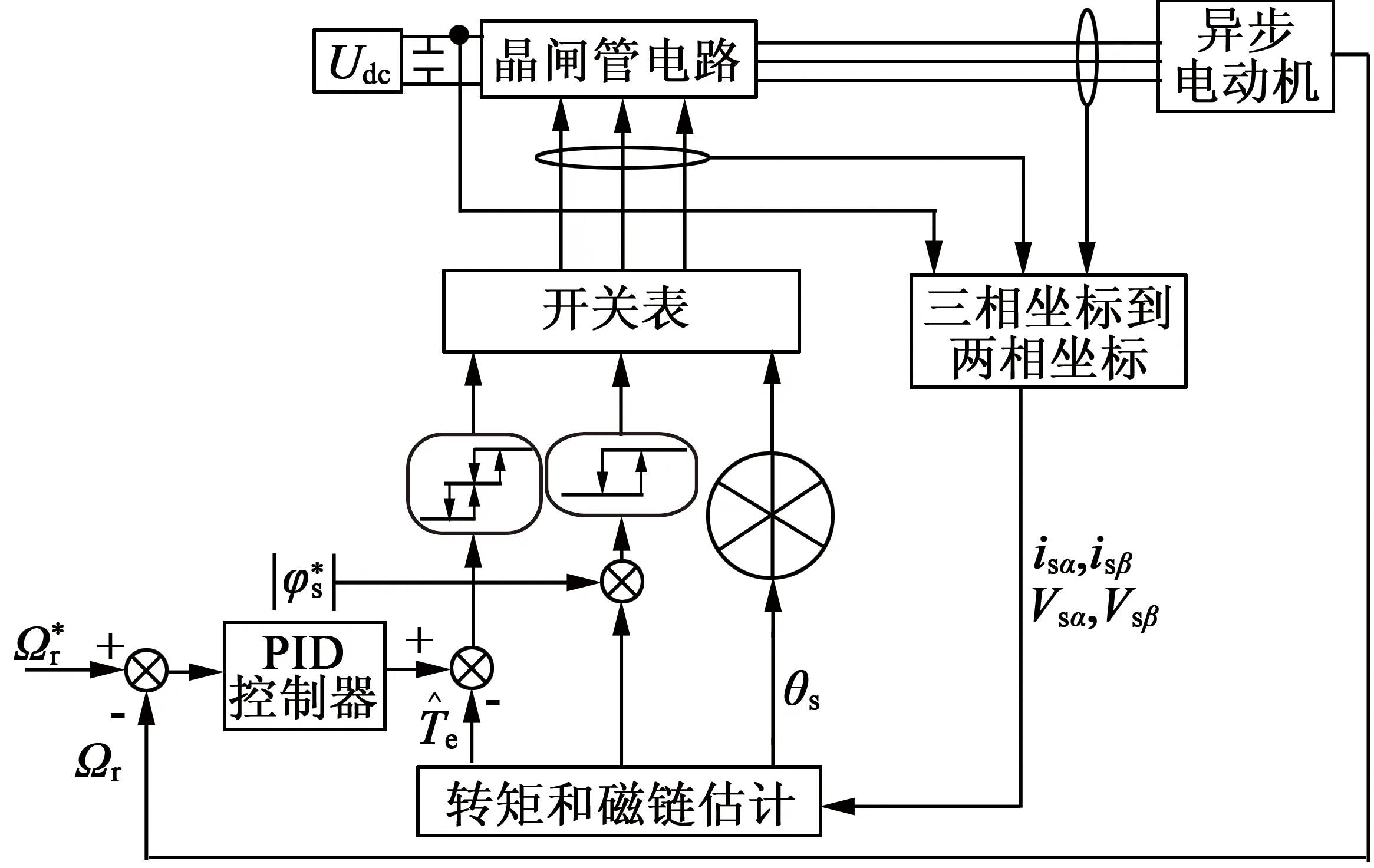
2.2 异步电动机的模型描述
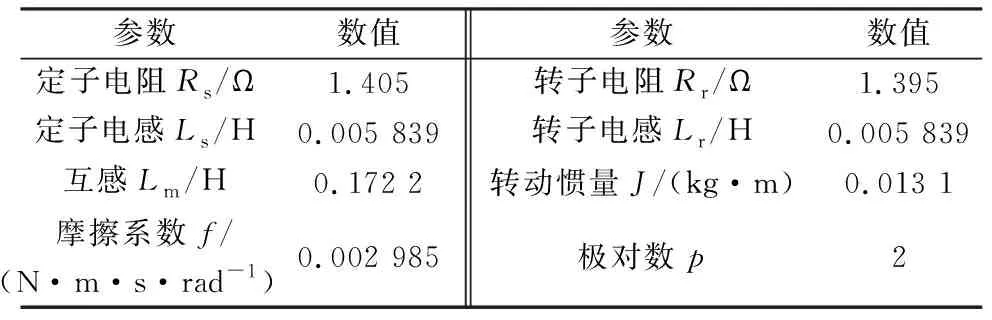
2.3 仿真结果
3 结 语
