基于灰色多项式回归组合模型的维修器材需求预测方法研究

2019-02-25于战果李世民

兵器装备工程学报 2019年1期

张磊，于战果，李世民

(1.陆军边海防学院，西安 710108； 2.陆军军事交通学院，天津 300161；3.中国人民解放军63963部队，北京 100072)

一直以来，装备维修器材的消耗需求预测都作为装备保障的重要环节而倍受关注[1-4]，其基本过程是基于历史数据，采用适当模型，进而推算其在下一阶段所需的器材消耗数量[1-8]。对于辅助决策工作而言，具有极其重要的意义。

由于影响作用不同历史时期的维修器材消耗量的因素很多，作用规律复杂且历史数据有限[1-3,5-8]，因此大样本需求量的模型并不适用。在这种情况下，灰色GM(1,1)模型得到了广泛使用[1-3,5-8]。该模型非常适合用于处理具有“小样本”、“贫信息”特点的不确定性复杂系统问题。

灰色GM(1,1)模型认为，系统内的数据积累和发展一般都存在能量的积累、存储和释放等过程，加之生成数列一般都有较强的指数变化趋势，所以灰色系统理论指出，离散的随机数经过累加生成变为随机性被显著削减的带有指数变化规律的生成数列，进而运用指数形式函数构建预测模型。但是在维修器材预测的实际运用中，由于随机因素的作用，数据列叠加后随机特性消除并不彻底，造成实际数据围绕预测曲线上下波动较大的情况[1-4]，这种“波动”可以通过拟合值和实际值之间的差值(残差)来体现，因此很多研究通过运用各类模型针对不同历史值的残差进行分析，并推算下一阶段的残差作为修正值，对灰色GM(1,1)模型的预测结果进行修正，提高预测准确率。如运用Markov模型预测灰色GM(1,1)模型的残差修正值[2-3]；运用BP神经网络模型预测灰色GM(1,1)模型的残差修正值[1]；运用傅里叶变换模型预测灰色GM(1,1)模型的残差修正值等[5]。

然而，以上对于灰色GM(1,1)模型的运用仅仅适用于在序列累加后数据“大体上”呈指数函数规律变化的情况[7]。不适用于具有复杂函数形式规律的情形。为更加准确地反映数据列的变化规律，部分学者运用灰色线性回归组合模型[8-9]体现并拟合出了指数函数规律和线性函数规律叠加序列的情形，取得了很好的效果。但是在随机特性更加明显的装备维修器材需求变化序列中显然不止这两种规律，应该是更为复杂的函数形式。因此本文运用灰色多项式回归组合模型深入挖掘数据列中除指数函数规律外的复杂变化规律，为各类基于灰色GM(1,1)模型残差修正模型的广泛应用奠定基础。

由于灰色线性回归模型[8-9]中通过序列累减的方式消除掉组合模型的线性函数项部分，运用求比值的方法消除指数函数的部分常系数以及变量部分，最后通过求对数值的方法确定指数函数的常系数。然而，这种方法对于数据列的要求较为苛刻，一旦累减序列出现负值时，便不能通过求对数的方法确定系数，而这种情况在实际预测时十分常见，显然在运用灰色多项式回归组合模型进行维修器材需求预测时不能够运用这种方法确定系数。

本文运用函数的Taylor级数展开形式表示任意复杂函数并论证了灰色多项式回归模型的合理性，通过推导给出了组合模型指数项系数的求解方法，最后运用最小二乘法确定灰色多项式回归模型中的各项系数。

算例结果表明：该模型的拟合效果较传统灰色GM(1,1)模型以及传统灰色线性回归模型有明显提高，且随着拟合采用项数增加，拟合精度也越高，证明了该模型的有效性和实用性。

1 灰色多项式回归组合预测模型的建立

1.1 灰色GM(1,1)模型

灰色GM(1,1)模型是各类预测中经常用到的模型之一[7]，假设一维原始序列为{x(0)(k)}，k=1,2,…,n。其预测式可以表示为[7]

(1)

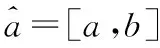
(2)

其中：

z(k)=[x(k)+x(k-1)]/2

其中，N为样本个数。由(1)式确定的发展系数a反应了维修器材消耗量的发展态势，若a< 0，则说明器材消耗数量的发展态势是增长的，a的绝对值越大，增长越快；若a> 0，说明数据的态势是减小的，a越大，减小越快。

1.2 灰色多项式回归组合预测模型的形式[8-9]

由于方程式(1)的预测形式可以记为

其中：C1=x(0)(1)-b/a,C2=b/a,-a=v；可以看出，预测式(1)本质上为一个指数函数。

用线性回归方程Y=aX+b及指数方程Y=aeX的和的形式来拟合叠加生成序列{x(1)(t)}，因此便得到灰色线性回归组合模型的基本形式：

(3)

其中，C1、C2、C3和v均为模型的待定系数，由式(3)可以看出，灰色线性回归组合模型可以很好地同时反映出叠加序列{x(1)(t)}中指数和线性的变化规律。

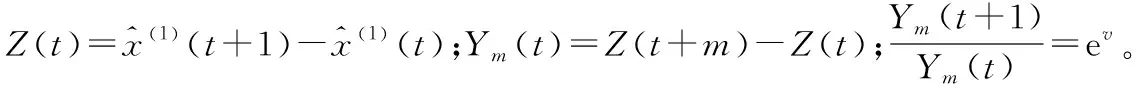
因此有：

(4)

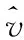
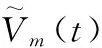
除单一指数函数规律和线性函数外，维修器材需求数据的变化往往体现出更为复杂的函数规律。假设除单一指数函数规律外，随机序列一次累加后所体现出的复杂规律的函数为一个关于时间t的连续函数f(t)。用函数方程Y=f(X)及指数方程Y=aeX的和的形式来拟合叠加生成序列{x(1)(t)}：

(5)

同时，f(t)可以展开为其Taylor级数形式：

f(t)=f(t0)+f′(t0)(t-t0)+…+

其中，Rn(t)为Taylor级数的余项，是(t-t0)n的高阶无穷小项，f(t0)及其在点t0处的各阶导函数值f(n)(t0)(n=1,2,…)均可视为常数。在展开、化简、合并同类项并忽略高阶无穷小项后，函数f(t)可以近似表示为n阶多项式的形式：

f(t)=C2+C3t+C4t2+…+Cn+2tn

因此灰色多项式回归组合模型的形式(即式(5))可以表示为

(6)

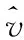
1.3 模型灰色发展系数的确定

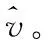
这主要是由于函数(6)为变量t的连续函数，而式(6)所需要拟合的函数则是仅仅“大体上”呈现出式(6)变化规律的随机离散值点，其随机特性使得序列累减后求得级比值小于0的情况经常发生。因此，传统灰色线性回归组合模型中用于确定指数系数的方法并不适用于维修器材消耗需求的预测。

由1.2节的论述可以知道，灰色GM(1,1)模型的预测式可表示为

(7)

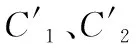
虽然式(6)和式(7)描述的为不同类型的曲线，但均是用于拟合同一组随机离散点的近似曲线，两曲线在相同时刻带入拟合方程的点相同。也就是说，在理想状况下，两曲线重合，且均经过序列{x(1)(k)}上各点。在一般状况下，两类曲线的具体形式均是通过拟合随机序列{x(1)(k)}的最小二乘法得到，两曲线也是大致接近的，因此可以近似认为

(8)

对式(8)两端求n+1阶导可得：

化简后可得：

(9)

因为式(9)左侧应为常数，所以有：

v′=v

(10)

由式(10)可以知道，灰色多项式回归模型的指数项的指数系数可以通过求解灰色GM(1,1)模型得到：

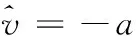
(11)

虽然将式(8)两端求高阶导可能产生较大误差，但在模型实际使用中，受历史数据量的限制，不可能使用项数较多的多项式拟合，因而避免了求高阶导数而得到指数系数v的情形。

同时，虽然式(11)为近似得到，但a为序列的灰色发展系数，仅反应随机序列的发展趋势，并不影响组合模型的整体拟合精度。由此可知，v′可以视为灰色多项式回归组合预测模型的灰色发展系数。

1.4 模型待定系数的确定

由于N为样本个数，可以运用最小二乘法确定式(6)中的待定系数：

(12)

可以看出，当C4=C5=…=Cn+2=0时，式(6)退化为灰色线性回归组合模型。当C3=C4=…=Cn+2=0时，式(6)退化为灰色GM(1,1)模型。由此，灰色多项式回归组合模型解决了灰色序列指数规律和复杂函数规律叠加的问题。

在实际预测应用中，系数Cn(n=1,2,…,n+2)均起着修正拟合并提高精度的作用，均描述着随机灰色作用因子对于时间序列作用[10]的结果。因此均可视为灰色作用量。

进行累减还原得到预测值：

(k=1,2,…,N)

(13)

1.5 残差和相对误差

(14)

在模型使用过程中，模型所使用拟合的项数越多，就越接近式(6)，取得的拟合相对误差就会越小。但是在维修器材需求预测中，数据通常体现出小样本的特点，因此拟合方程数量有限，不可能采用过多的项进行拟合。当拟合项数过多时，不仅会因拟合方程需求数量过多而降低拟合效果，甚至可能导致拟合多项式系数无法求解的情况。

2 实例分析

分别选取2项式模型、3项式模型和4项式模型拟合数据，三类模型可统一表示为

(15)

式(15)中当C5=C4=0时，式(15)为2项式模型(线性回归组合模型)。C5=0时，式(15)为3项式模型。均不为0时，式(15)为4项式模型。由式(12) 、式(13)计算系数可得结果如表1所示。

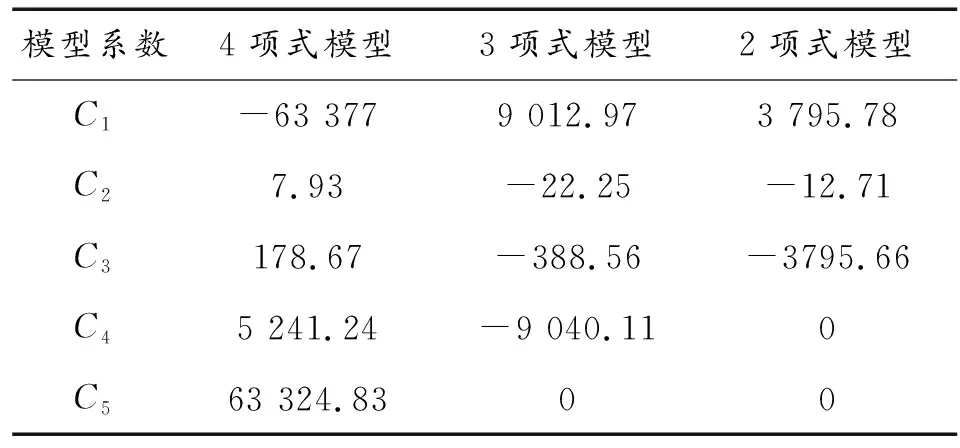
表1 各类灰色多项式回归模型系数

将表1中各阶模型系数结果分别带入式(15)计算拟合结果，由式(14)计算相对误差，同时计算灰色GM(1,1)模型拟合结果，结果见表2。

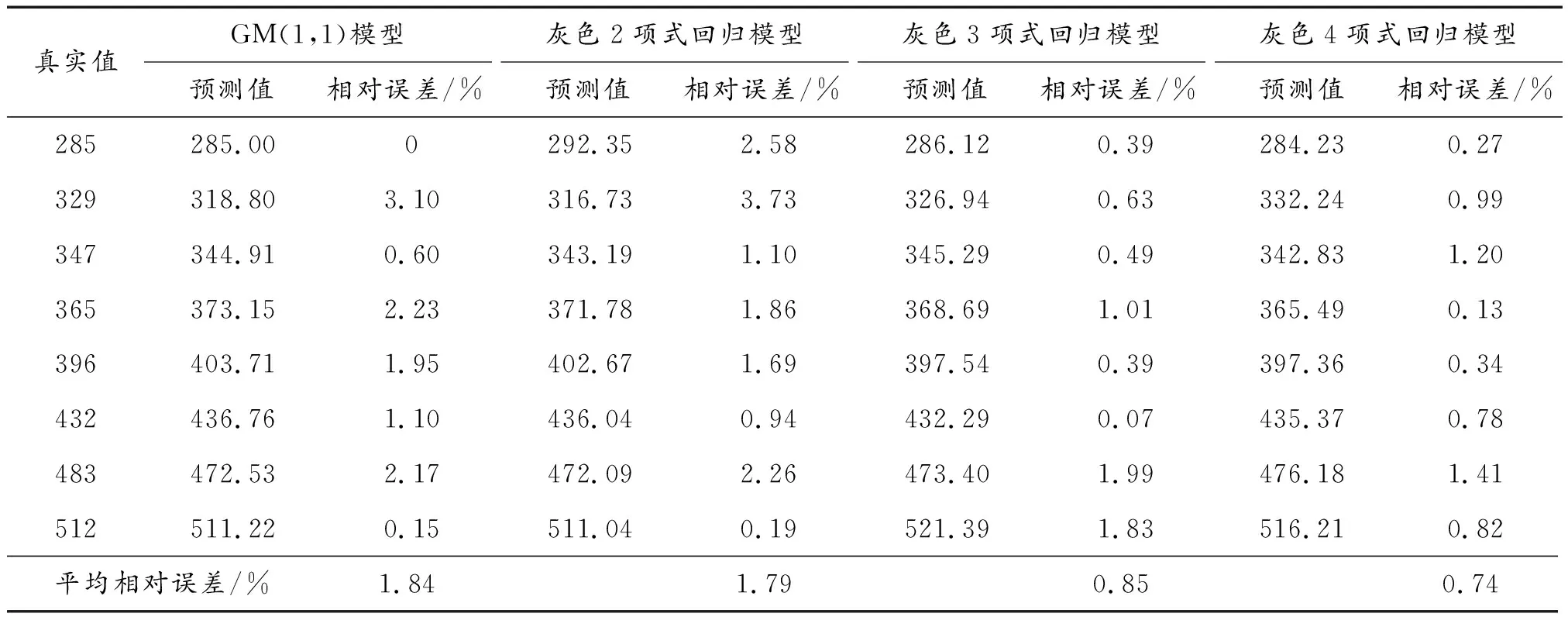
表2 不同模型预测计算结果

由计算结果(表2)可以看到，灰色多项式回归组合模型的拟合相对误差较灰色GM(1,1)模型有了显著的减小，且随着拟合多项式项数的增加，拟合精度逐渐提高。特别是当拟合多项式为3项和4项式时，平均相对误差由1.84%和1.79%降为0.85%和0.74%。说明灰色多项式回归模型能够更好地挖掘变化序列中的复杂函数形式变化规律，提高拟合精度。同时，随着灰色多项式拟合项数的增加，运用最小二乘法拟合求解所需的数据量也就越多，但在实际运用时数据数量均是固定的，所以使用的拟合项数过多反而会影响拟合效果。本例中数据个数为8个，仅能提供8个拟合方程，当使用灰色8项回归组合模型时将产生9个未知系数，则无法通过最小二乘法得到结果。