弹丸姿态解算初始地磁分量误差分析

鲍广建，丁立波，张 合

(南京理工大学 机械工程学院， 南京 210094)

智能弹药是武器信息化的重要组成部分，实现常规弹药的精确制导打击，对于掌握战争的主动权，有着至关重要的作用[1-2]。常规弹药的制导一般采取弹道修正的办法。在发射前，测量好与目标的相对距离和角度；在飞行过程中，进行计算自身姿态，实时调整自身，以确保落点正好落在预定目标处。计算自身姿态的方法，一般采取地磁传感器、陀螺仪、MEMS加速度计等[3-4]。基于地磁的解算方法，以其稳定、干扰性小、抗过载能力强、可靠性高、成本低的特点，成为近年来制导弹药的发展方向之一[5]。基于地磁信息的弹药姿态算法，是通过已知发射地区的地磁三分量信息和实际的弹丸上的地磁分量，弹体坐标系和地面坐标系之间存在的换算关系，其变换矩阵是以弹丸的三个姿态角为基准。解算时，需要知道地磁信息和弹丸的其中一个姿态角去解算另外两个姿态角，方便进行调整。目前，一般利用电脑软件信息，预先获取发射地的地磁三分量。地磁三分量准确度影响着弹丸姿态角准确度。本研究针对地磁三分量对弹丸姿态角的影响进行误差分析。

1 弹丸姿态解算方法

1.1 坐标系定义与变换

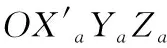
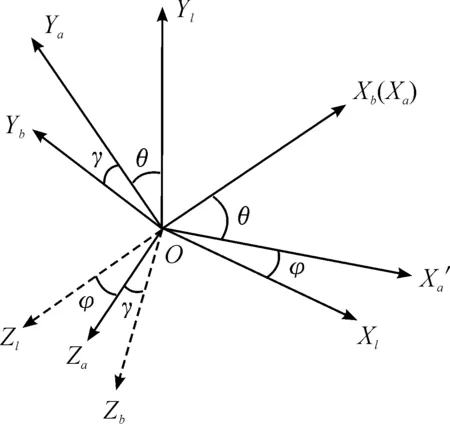
图1 坐标系

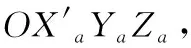
(1)

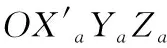
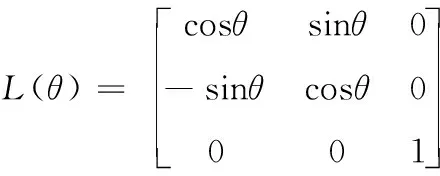
(2)

最后由坐标系OXaYaZa绕OXa正向旋转γ角度得到OXbYbZb，此时的转换矩阵为

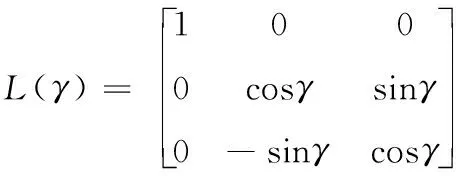
(3)

由上面三个矩阵可以得到总的变换矩阵为

L(γ,θ,φ)=L(γ)L(θ)L(φ)

(4)

即是

L(γ,θ,φ)=

(5)

其中：γ为滚转角；θ为俯仰角；φ为偏航角。

1.2 姿态角解算方法

由坐标转换分析可得，在知道大地坐标系的矢量Hl和弹体坐标系的矢量Hb的情况下，可以获得三个姿态角之间的关系式

(6)

三个方程含有三个未知数，因此，还需要知道三个姿态角中的一个才能进行求解。对于常规弹药来说，打击目标所处位置一般不变，因此弹道轨迹是一个在二维平面上的抛物线。弹丸的偏航角变化小甚至不变，而俯仰角需要经历一个由正到负的过程，滚转角更是在每时每刻的变化。偏航角通常在未发射弹体前便已经确认好，故采取已知偏航角的方法，根据偏航角去推到弹体的俯仰角和滚转角[8]。

对第一个关系式进行化简，再进行辅助角变换反推可得

(7)

第二个关系式乘以sinγ与第三个关系式乘以cosγ相加，辅助角公式化简后直接求得

(8)

式中：arctan的取值为[0,360°)；arccos的取值为[0,180°]。三个姿态角取值范围依次为0≤γ<360°，-90°<θ<90°和-180°≤φ<180°。

由此可见，俯仰角与滚转角是与地磁三分量和偏航角有关的函数，地磁场分量的准确性影响到弹体姿态的测量。在地磁分量不准确的情况下，俯仰角与滚转角的精度就会收到一定的影响。

1.3 姿态角基于初始地磁分量的误差分析

弹体的具体姿态解算受初始装定进弹体的地磁三分量影响。为了提高姿态角的精度，有必要研究地磁三分量对解算姿态角的具体误差。

根据式(7)，θ是关于Xl、Yl、Zl的函数，且三个变量之间相互独立。为了研究各个变量之间的影响，最直观的就是预先知道真值，固定其余两个变量，只变动其中一个变量，将改动过的变量计算出来的值与采用真值计算出来的值进行对比，即是

Δθ=θ′-θ0

(9)

其中：Δθ是俯仰角的误差；θ′是改变一个变量后计算出来的俯仰角值；θ0是真值计算出来的俯仰角值。

同理可得

Δγ=γ′-γ0

(10)

其中：Δγ是滚转角的误差；γ′是改变一个变量后计算出来的滚转角值；γ0是真值计算出来的滚转角值。

研究误差影响还可以对其求导,进行局部线性化[9]。以x对姿态角的影响为例。将式(15)中θ记作θ=f(x)。将θ=f(x)在x=x0处按泰勒公式展开。在Δx很小的情况下，可以将高次多项式忽略，进行局部线性化可得

(11)

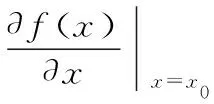
(12)

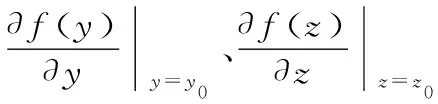
同理，对于滚转角，将式(8)中γ记作g(x,y,z),同样在其真值处进行泰勒展开，忽略其高次多项式，可得

(13)

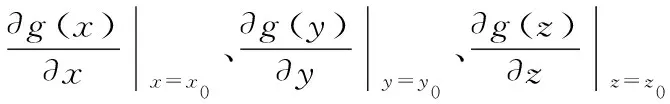
观察分析这些式子，在一定程度下，Δθ与Δx、Δy、Δz近似为线性关系，Δγ与Δx、Δy、Δz也呈现线性关系。为了具体研究这个线性影响量的大小，需要求出这些方程的导数。

对式(7)、式(8)分别求导得

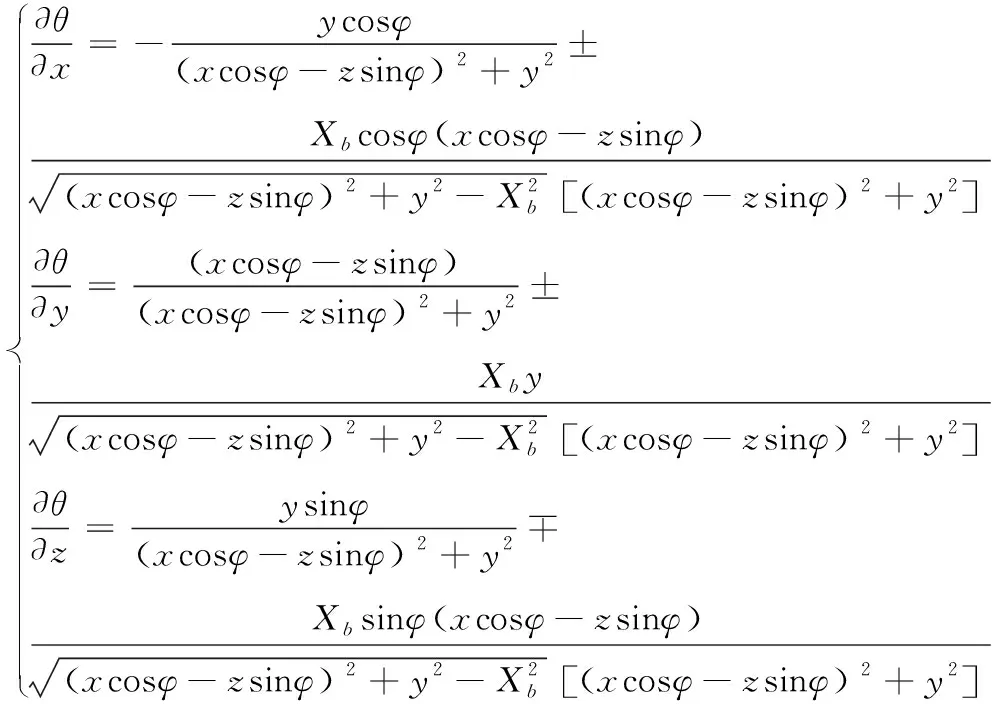
(15)

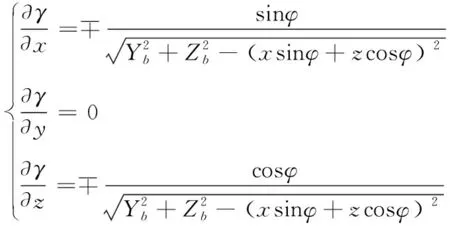
(16)

x、y、z之间三者的累积绝对误差为相加之和[10]，即是

通过给出一定的已知数值，便可以通过绝对误差方程去计算误差的大小。

2 仿真分析

为了直观看出绝对误差大小，现采取MATLAB绘制其绝对误差曲线。假设弹丸向正北方向发射，以南京某地为例，其纬度为北纬32°01′33″，经度为东经118°50′52″，海拔为36.4 m，根据WMM2015模型计算得出地磁三分量的真值为X=32 725.1 nT,Y=-3 264.0 nT,Z=37 529.7 nT。由于地磁分量真值误差不会太大。假设其变化在真值上下500 nT浮动，因此将其范围设置x∈[32 200, 33 200]，y∈[-3 700, -2 700],z∈[37 000, 38 000],以此来观察详细的误差影响。用传感器测出一些通常状态下的地磁分量值来作为Xb、Yb、Zb的值，不同偏航角下，有不同的实测值。本研究采取偏航角为-180°、-135°、-90°、-45°、0°、45°、90°、135°的情况下，绘制曲线。

直接比较法，取代表性图像如图2、图3所示。由图2、图3可知，在设定的变化范围内，θ关于X的绝对误差大小不超过0.15°；θ关于Y的绝对误差大小不超过0.000 5°；θ关于Z的绝对误差大小不超过0.25°。γ关于X的绝对误差大小不超过0.2°；因为γ是关于X,Z的函数，与Y不相关，故在图像上,Y对于γ的误差没有影响。γ关于Z的绝对误差大小不超过0.15°。X与Z的影响较大，Y的影响因素较小。需要注意的是，在图像上出现了部分水平线，是因为在某些姿态下，分量的绝对误差导致了计算出现虚数，即是不存在实数解。在某些情况下，传感器测出的数值，遇上了不够准确的地磁分量后，会出现无解的情况，此时便解算不出姿态角。

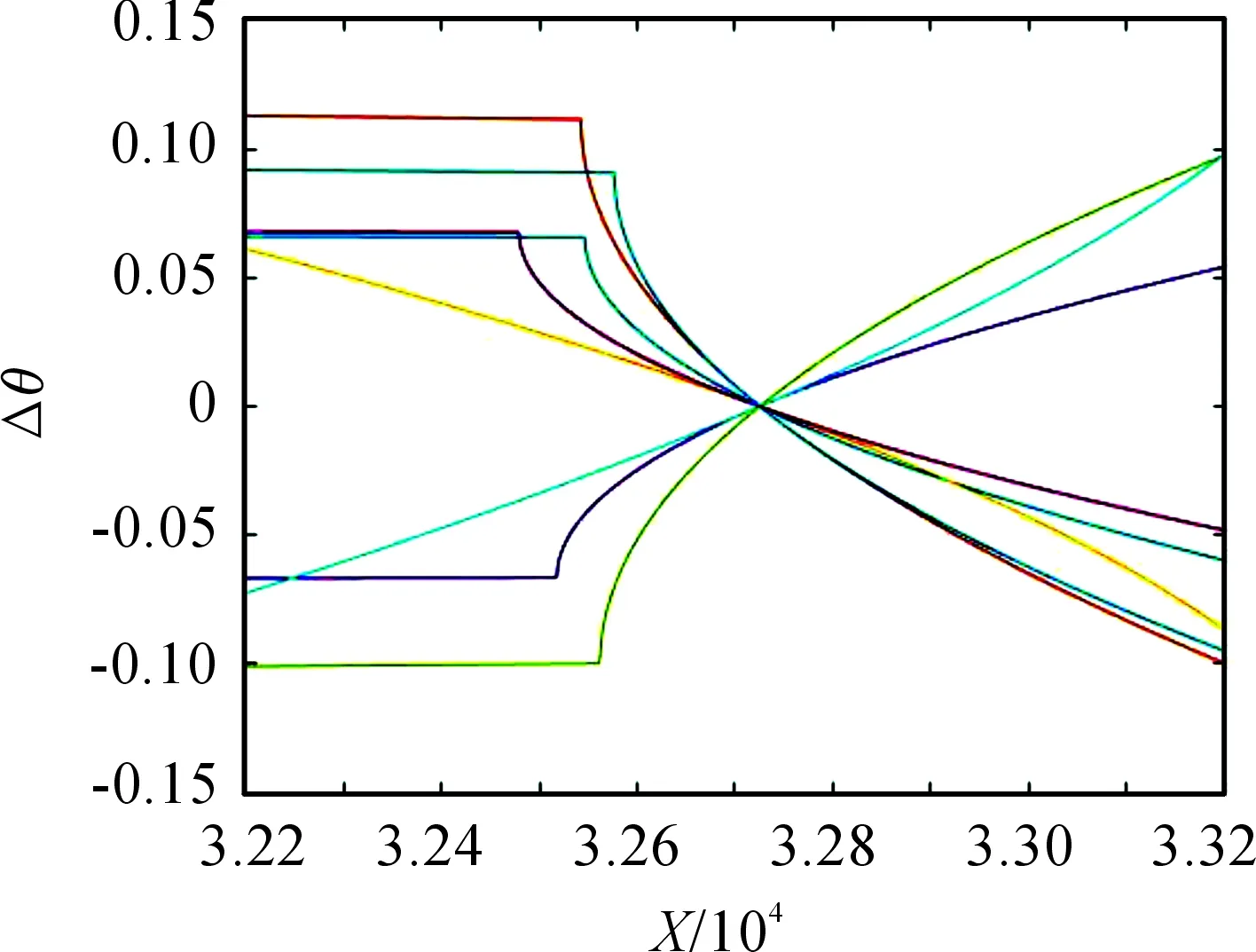
图2 θ关于x的绝对误差

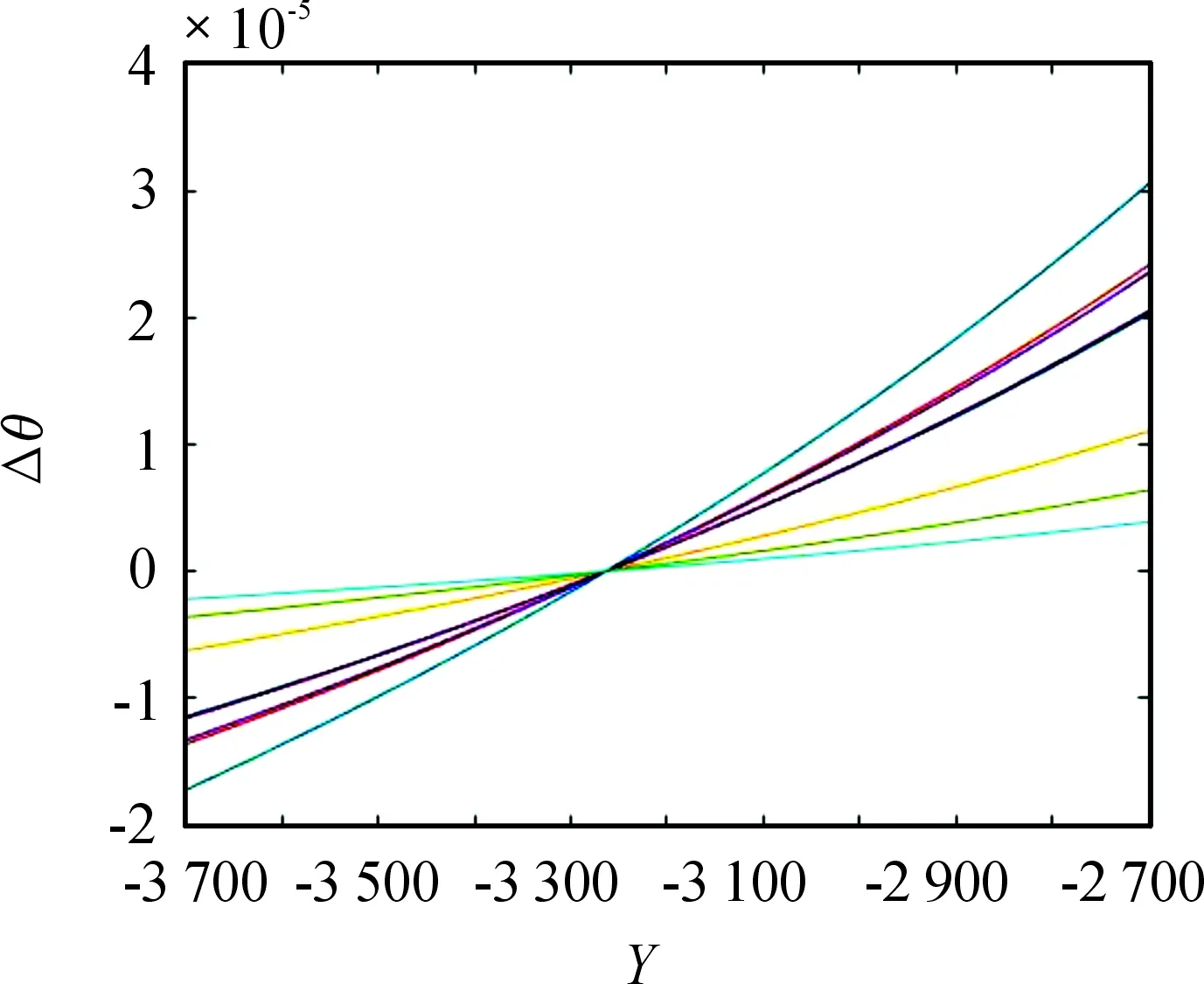
图3 θ关于y的绝对误差

对于求导法，因为其真值确定，故前面的系数也是确定的，所以误差图像均呈现一个线性，故取一个代表性图像。

如图4所示，在设定的变化范围内，θ关于X的误差大小不超过0.2°；θ关于Y的误差大小不超过0.000 5°；θ关于Z的误差大小不超过0.2°。γ关于X的误差大小不超过0.2°；γ关于Y的误差为0，γ关于Z的误差大小不超过0.2°。

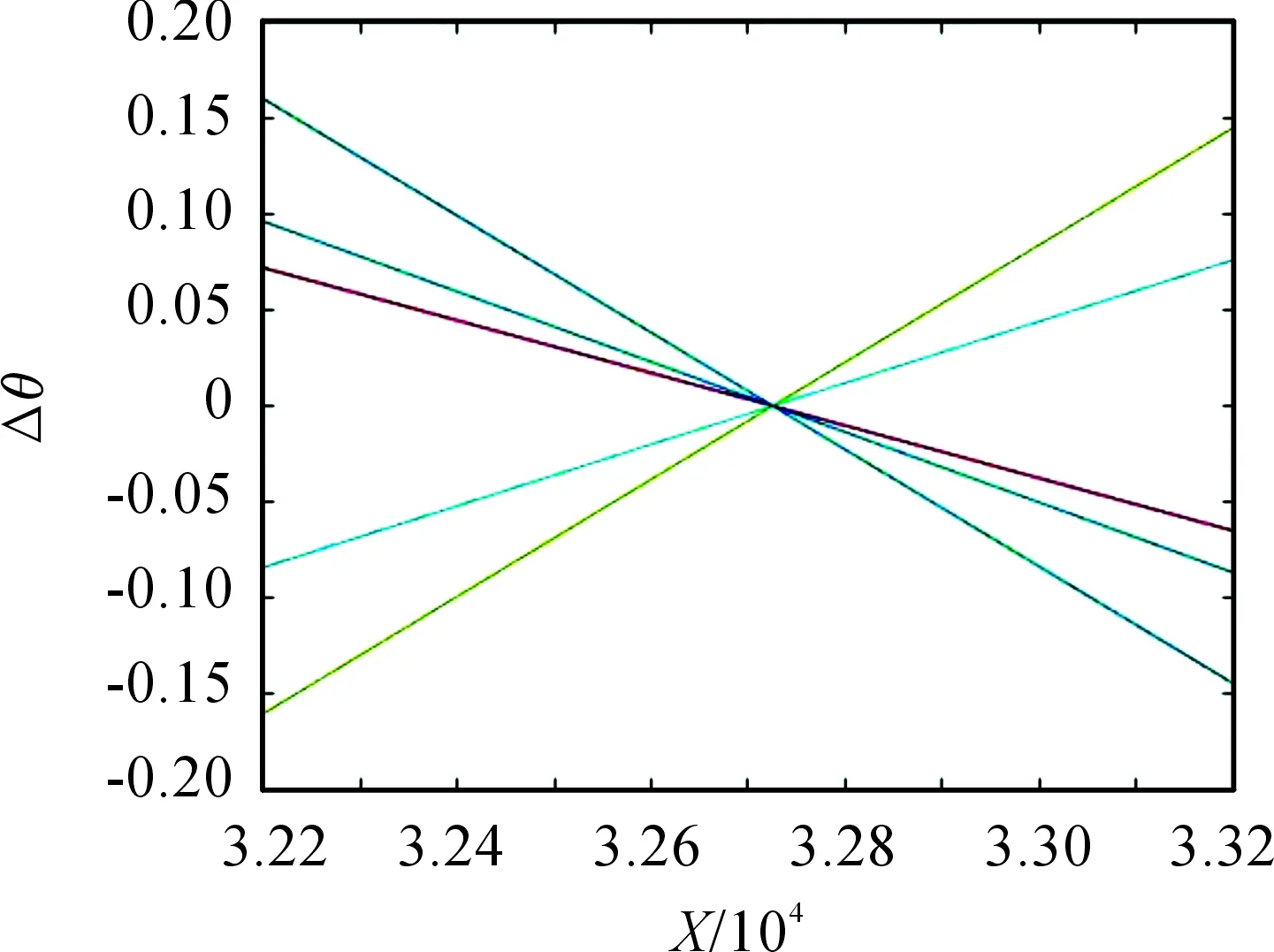
图4 求导法θ关于x的绝对误差

由于导数法存在着两种不同的符号，在另一种符号下，θ关于X的绝对误差大小不超过0.2°；θ关于Y的绝对误差大小不超过0.1°；θ关于Z的绝对误差大小不超过0.2°。γ关于X的绝对误差大小不超过0.2°；γ关于Y的绝对误差为0，γ关于Z的绝对误差大小不超过0.2°。

综上所述，地磁分量的准确度影响着姿态角角度。角度误差与单分量绝对误差呈一定的线性关系。与真值相差500 nT情况下，姿态角的绝对误差不超过0.2°。三者间绝对误差总值不会超过0.65°。地磁分量相差越大，姿态角绝对误差越大，某些情况下，甚至存在无解状态，给弹体导航带来影响。

3 结论

以基于地磁解算姿态的方法为背景，分析了姿态角解算方法，利用已知当地地磁分量及实时地磁分量和偏航角，计算出俯仰角和滚转角。此外对姿态角的绝对误差建立了基于初始地磁分量的绝对误差模型。通过分析方程可知，姿态角的绝对误差与初始地磁分量绝对误差基本呈线性。总体而言，在正常情况下初始地磁分量对姿态角的影响大概在1°以内，但在某些特殊情况下存在无解。因此，一个良好的初始地磁分量精度对智能弹药的发展也起着重要作用。